Sepupu relatif apa, penjelasan, contoh

Dipanggil sepupu relatif (Coprmimos atau sepupu relatif antara satu sama lain) kepada mana -mana sepasang nombor keseluruhan yang tidak mempunyai pembahagi biasa, kecuali 1. Dalam erti kata lain, dua nombor keseluruhan adalah sepupu relatif jika dalam pecahan mereka dalam nombor perdana, mereka tidak mempunyai faktor yang sama.

Sebagai contoh, jika 4 dan 25 dipilih, penguraian dalam faktor utama masing -masing adalah 2 ² dan 5 ² masing -masing. Seperti yang dapat dilihat, mereka tidak mempunyai faktor yang sama, oleh itu, 4 dan 25 adalah sepupu relatif.

Sebaliknya, jika anda memilih 6 dan 24, ketika membuat pecahan mereka dalam faktor utama, diperolehi 6 = 2*3 dan 24 = 2³*3.

Seperti yang dapat dilihat, kedua -dua ungkapan terakhir ini mempunyai sekurang -kurangnya satu faktor biasa, oleh itu, mereka bukan sepupu relatif.

Ciri -ciri sepupu relatif

Perincian yang mesti dijaga.

Sebaliknya, definisi di atas dapat diringkaskan seperti berikut: Dua bilangan bulat "A" dan "B" adalah sepupu relatif jika, dan hanya, pembahagi maksimum maksimum ini adalah 1, iaitu, MCD (A, B ) = 1.

Dua kesimpulan segera definisi ini ialah:

-Jika "a" (atau "b") adalah nombor utama, maka mcd (a, b) = 1.

-Jika "A" dan "B" adalah nombor utama, maka MCD (a, b) = 1.

Iaitu, jika sekurang -kurangnya salah satu nombor yang dipilih adalah nombor utama, maka pasangan nombor adalah sepupu relatif.

Ciri -ciri lain

Hasil lain yang digunakan untuk menentukan sama ada dua nombor adalah sepupu relatif:

-Sekiranya dua nombor keseluruhan berturut -turut, maka ini adalah sepupu relatif.

-Dua nombor semula jadi "A" dan "B" adalah sepupu relatif jika, dan hanya jika, nombor "(2^a) -1" dan "(2^b) -1" adalah sepupu relatif.

-Dua nombor keseluruhan "a" dan "b" adalah sepupu relatif jika, dan hanya jika, ketika grafik titik (a, b) dalam satah Cartesian, dan membina garis yang melewati asal (0.0) dan (a , b), ini tidak mengandungi sebarang titik dengan keseluruhan koordinat.

Contoh

1.- Pertimbangkan keseluruhan nombor 5 dan 12. Penguraian dalam faktor utama kedua -dua nombor adalah: 5 dan 2 ²*3 masing -masing. Kesimpulannya, MCD (5,12) = 1, oleh itu, 5 dan 12 adalah sepupu relatif.

2.- Biarkan nombor -4 dan 6. Kemudian -4 = -2² dan 6 = 2*3, supaya MCD (-4,6) = 2 ≠ 1. Sebagai kesimpulan -4 dan 6 bukan sepupu relatif.

Jika garis yang melewati pasangan yang diperintahkan (-4,6) dan (0.0), dan untuk menentukan persamaan garis tersebut, dapat disahkan bahawa ini melalui titik (-2,3).

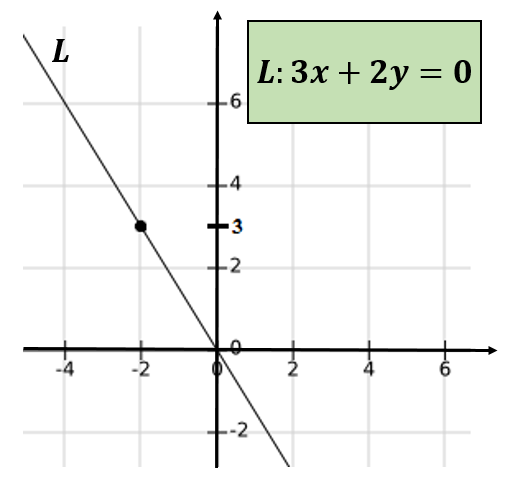
Sekali lagi, disimpulkan bahawa -4 dan 6 bukan sepupu relatif.

3.- Bilangan 7 dan 44 adalah sepupu relatif dan dapat disimpulkan dengan cepat terima kasih kepada apa yang telah dikatakan di atas, kerana 7 adalah nombor utama.

4.- Pertimbangkan nombor 345 dan 346. Menjadi dua nombor berturut -turut, disahkan bahawa MCD (345,346) = 1, oleh itu, 345 dan 346 adalah sepupu relatif.

5.- Jika nombor 147 dan 74 dipertimbangkan, maka ini adalah sepupu relatif, sejak 147 = 3*7² dan 74 = 2*37, oleh itu, MCD (147,74) = 1.

6.- Bilangan 4 dan 9 adalah sepupu relatif. Untuk menunjukkannya, anda boleh menggunakan pencirian kedua yang disebutkan di atas. Sesungguhnya, 2^4 -1 = 16-1 = 15 dan 2^9-1 = 512-1 = 511.

Nombor yang diperoleh adalah 15 dan 511. Penguraian dalam faktor utama nombor ini masing -masing adalah 3*5 dan 7*73, sehingga MCD (15,511) = 1.

Seperti yang anda lihat, menggunakan pencirian kedua adalah kerja yang lebih panjang dan lebih susah payah untuk mengesahkannya secara langsung.

7.- Pertimbangkan nombor -22 dan -27. Maka nombor -nombor ini boleh ditulis semula seperti berikut: -22 = -2*11 dan -27 = -3³. Oleh itu, MCD (-22, -27) = 1, SO -22 dan -27 adalah sepupu relatif.