Derivatif tersirat bagaimana mereka diselesaikan dan diselesaikan latihan

The derivatif tersirat Mereka adalah alat yang digunakan dalam teknik pembezaan yang digunakan untuk fungsi. Mereka memohon apabila tidak mungkin, di bawah kaedah biasa, melaksanakan pelepasan pemboleh ubah bergantung yang akan diperoleh. Pelepasan ini dilakukan berdasarkan pemboleh ubah bebas.

Contohnya, dalam ungkapan 3xy³ - 2y + xy² = xy, anda tidak boleh mendapatkan ungkapan yang mentakrifkan "y" bergantung pada "x". Jadi apabila ekspresi pembezaan dy/dx dapat diperoleh.

[TOC]

Bagaimana derivatif tersirat diselesaikan?

Untuk menyelesaikan implikasi, ia berdasarkan ungkapan tersirat. Contohnya: 3xy³ - 2y + xy² - Xy = 0. Ini telah dibersihkan dengan jelas, namun untuk berbuat demikian bukanlah syarat yang diperlukan untuk mendapatkan terbitan y mengenai x. Kemudian, setiap elemen diperolehi menghormati peraturan rantai untuk fungsi campuran:

3xy³ Ia terdiri daripada 2 pembolehubah, oleh itu d (3xy³) Ia akan dianggap sebagai terbitan produk fungsi.

D (3xy³)/dx = 3y³ + 3y².(3x) dan '= 3y³ + 9xy² dan '

Di mana elemen dan 'dikenali sebagai "dan sepupu"Dan Dy/Dx mewakili

-2y diperolehi mengikut undang -undang k.U = k.Atau '

D (-2y) = -2 dan '

Xy² Katakan satu lagi perbezaan yang terdiri daripada produk fungsi

D (xy²) = y² + 2xy dan '

-Xy adalah cara homolog

d (-xy) = -y -x dan '

Mereka digantikan dengan kesamaan, mengetahui bahawa derivatif sifar adalah sifar.

3y³ + 9xy² dan ' - 2 dan' + dan² + 2xy dan ' - y - x dan' = 0

Unsur -unsur yang mempunyai istilah dan 'dikumpulkan bersama di satu sisi persamaan

Boleh melayani anda: vektor colineal

3y³ + dan² - y = -9xy² dan ' + 2 dan' + x dan '

Faktor biasa dan 'pada anggota kesamaan yang betul diekstrak

3y³ + dan² - y = y '(-9xy² + x + 2)

Akhirnya, istilah yang berlipat ganda dan '. Dengan itu memperoleh ungkapan yang sepadan dengan derivatif tersirat y mengenai x.

dan '= dy/dx = (3y³ + dan² - y)/(-9xy² + x + 2)

Peraturan rantai

Dalam derivasi tersirat peraturan rantai selalu dihormati. Semua ungkapan pembezaan akan diberikan bergantung kepada pembolehubah bebas x. Supaya pembolehubah θ berbeza dari x mesti memasukkan istilah dθ/dx setelah diperolehi.

Istilah ini akan muncul hanya pada tahap pertama atau dengan eksponen sama dengan 1. Kualiti ini menjadikannya jelas di bawah kaedah pemfaktoran tradisional. Supaya ia menjadi mungkin untuk mendapatkan ungkapan yang mentakrifkan perbezaan dθ/dx.

Dalam Peraturan Rantaian, sifat progresif pembezaan atau proses derivatif ditunjukkan. Di mana untuk sebarang fungsi komposit f [g (x)], ungkapan pembezaan f mesti

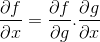
Pesanan operasi

Dalam setiap undang -undang formula atau derivasi yang digunakan, perintah pembolehubah mesti diambil kira. Kriteria yang dikaitkan dengan pemboleh ubah bebas dihormati, tanpa mengubah korelasi dengan pemboleh ubah bergantung.

Nisbah pemboleh ubah bergantung pada masa diperolehi diambil secara langsung.; Dengan pengecualian bahawa ini akan dianggap sebagai fungsi kedua, sebab itu kriteria peraturan rantai untuk fungsi campuran digunakan.

Ini dapat dibangunkan dalam ekspresi dengan lebih daripada 2 pembolehubah. Di bawah prinsip yang sama semua perbezaan yang merujuk kepada pembolehubah bergantung akan dilambangkan.

Boleh melayani anda: apakah panduannya? (Geometri)

Secara grafik kriteria yang sama ditangani yang mentakrifkan derivatif. Walaupun derivatif adalah cerun garis tangen ke lengkung dalam satah, selebihnya perbezaan kepunyaan pembolehubah bergantung (dy/dx, dz/dx) mewakili pesawat tangen kepada badan vektor yang diterangkan oleh fungsi pelbagai pembolehubah.

Tersirat fungsi

Dikatakan bahawa fungsi ditakrifkan secara tersirat, jika ungkapan y = f (x) boleh diwakili sebagai fungsi pembolehubah berganda f (x, y) = 0 manakala f ditakrifkan dalam satah r r².

3xy³ - 2y + xy² = x dan boleh ditulis dalam borang 3xy³ - 2y + xy² - Xy = 0

Memandangkan kemustahilan menjelaskan fungsi y = f (x).

Sejarah

Kalkulus pembezaan mula dilantik oleh pelbagai penyelidik matematik, sekitar abad ketujuh belas. Kali pertama disebutkan adalah melalui sumbangan Newton dan Leibniz. Kedua -duanya merawat kalkulus pembezaan dari sudut pandangan yang berbeza, tetapi menumpu dalam hasilnya.

Walaupun Newton memberi tumpuan kepada pembezaan sebagai kelajuan atau kadar variasi, pendekatan Leibniz lebih geometri. Boleh dikatakan bahawa Newton menyerang sangkaan yang ditinggalkan oleh Apollonius Perge dan Leibniz idea -idea geometri Fermat.

Terbitan tersirat muncul dengan segera apabila persamaan perbezaan dan komprehensif dipertimbangkan. Mereka memperluaskan konsep geometri Leibniz kepada r³ dan juga ruang multidimensi.

Aplikasi

Derivatif tersirat digunakan dalam pelbagai situasi. Mereka biasa dalam masalah kadar pertukaran antara pembolehubah yang berkaitan, di mana, bergantung kepada pengertian pengajian, pembolehubah akan dianggap bergantung atau bebas.

Mereka juga mempunyai aplikasi geometri yang menarik, seperti dalam masalah refleksi atau bayang -bayang, pada angka yang bentuknya dapat dimodelkan secara matematik.

Boleh melayani anda: persampelan kuota: kaedah, kelebihan, kekurangan, contoh

Mereka sering digunakan dalam bidang ekonomi dan kejuruteraan, serta dalam pelbagai penyiasatan fenomena semulajadi dan bangunan eksperimen.

Latihan yang diselesaikan

Latihan 1

Tentukan ungkapan tersirat yang mentakrifkan dy/dx

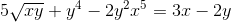
Setiap elemen berbeza dari ungkapan

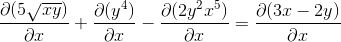
Menubuhkan peraturan rantai dalam setiap kes yang kompeten

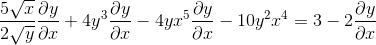
Mengumpulkan satu sisi persamaan unsur -unsur yang mempunyai dy/dx

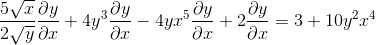
Adalah pemfaktoran menggunakan faktor biasa

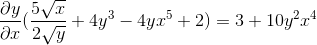
Dibersihkan dengan mendapatkan ungkapan yang dicari

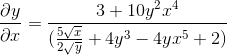
Latihan 2

Tentukan ungkapan tersirat yang mentakrifkan dy/dx

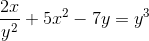
Menyatakan derivatif untuk dilaksanakan

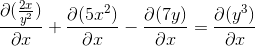
Secara tersirat memperoleh mengikut peraturan rantai

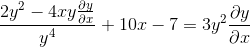
Pemfaktoran elemen umum

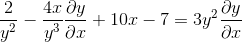
Mengumpulkan istilah dy/dx di satu sisi persamaan

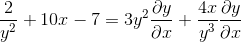
Faktor umum dengan elemen pembezaan

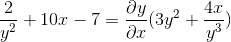
Kami membersihkan dan mendapatkan ungkapan yang dicari

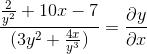
Rujukan

1. Kalkulus pemboleh ubah tunggal. Ron Larson, Bruce H. Edwards. Pembelajaran Cengage, 10 November. 2008
2. Teorem Fungsi Terbitan: Sejarah, Teori, dan Aplikasi. Steven G. Krantz, Harold R. Taman. Springer Science & Business Media, 9 Nov. 2012
3. Analisis multivariable. Sable Shirali, Hararkrishan Lal Vasudeva. Springer Science & Business Media, 13 Disember. 2010
4. Dinamik Sistem: Pemodelan, Simulasi, dan Kawalan Sistem Mekatronik. Dekan c. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7 mar. 2012
5. Kalkulus: Matematik dan pemodelan. William Bauldry, Joseph R. Fiedler, Frank R.Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1 Januari. 1999