Penguraian tambahan

The penguraian tambahan integer positif adalah untuk menyatakannya sebagai jumlah dua atau lebih nombor positif. Oleh itu, kita mempunyai nombor 5 yang dapat menyatakannya sebagai 5 = 1+4, 5 = 2+3 atau 5 = 1+2+2. Setiap cara menulis nombor 5 ini adalah apa yang akan kita sebut penguraian tambahan.

Jika kita memberi perhatian, kita dapat melihat bahawa ungkapan 5 = 2+3 dan 5 = 3+2 mewakili komposisi yang sama; Kedua -duanya mempunyai nombor yang sama. Walau bagaimanapun, hanya untuk keselesaan biasanya ditulis setiap iklan berikutan kriteria dari yang paling sedikit ke yang paling besar.

Penguraian tambahan

Sebagai contoh lain, kita boleh mengambil nombor 27, yang boleh kita nyatakan sebagai:

27 = 7+10+10

27 = 9+9+9

27 = 3+6+9+9

27 = 9+18

Penguraian Aditif adalah alat yang sangat berguna yang membolehkan kita mengukuhkan pengetahuan kita mengenai sistem penomboran.

Penguraian bahan tambahan kanonik

Apabila kita mempunyai bilangan lebih daripada dua angka, satu bentuk tertentu yang mengurasnya adalah dalam gandaan 10, 100, 1000, 10,000, dll., yang membuatnya. Cara menulis mana -mana nombor dipanggil penguraian tambahan kanonik. Sebagai contoh, nombor 1456 boleh menguraikannya seperti berikut:

1456 = 1000 + 400+ 50 + 6

Sekiranya kita mempunyai nombor 20 846 295, penguraian tambahan kanonik anda akan menjadi:

20 846 295 = 20 000 000 + 800 000 + 40 000 + 6000 + 200 + 90 +5.

Terima kasih kepada penguraian ini, kita dapat melihat bahawa nilai digit yang diberikan diberikan oleh kedudukan yang ditempati. Mari kita ambil sebagai contoh nombor 24 dan 42:

24 = 20 + 4

42 = 40 +2

Di sini kita dapat melihat bahawa dalam 24 2 mempunyai nilai 20 unit dan pada 4 nilai 4 unit; Sebaliknya, pada 42 4 mempunyai nilai 40 unit dan 2 dari dua unit. Oleh itu, walaupun kedua -dua nombor menggunakan digit yang sama, nilai mereka sama sekali berbeza dengan kedudukan yang mereka hadapi.

Boleh melayani anda: x kuadrat

Aplikasi

Salah satu aplikasi yang boleh kita berikan kepada penguraian tambahan adalah dalam jenis demonstrasi tertentu, di mana ia sangat berguna untuk melihat integer positif sebagai jumlah orang lain.

Contoh Teorem

Mari kita ambil sebagai contoh teorem berikut dengan demonstrasi masing -masing.

- Menjadi z keseluruhan 4 digit, maka z boleh dibahagikan dengan 5 jika angka sepadan dengan unit adalah sifar atau lima.

Demonstrasi

Mari kita ingat apa itu Divisibilitas. Sekiranya kita mempunyai nombor keseluruhan "a" dan "b", kita mengatakan bahawa "" membahagikan "b" jika ada integer "c" seperti b = a*c.

Salah satu sifat pembahagian memberitahu kita bahawa jika "A" dan "B" boleh dibahagikan antara "C", maka penolakan "A-B" juga.

Menjadi z keseluruhan 4 digit; Oleh itu, kita boleh menulis kepada z dan z = abcd.

Menggunakan penguraian bahan tambahan kanonik kita perlu:

Z = a*1000 + b*100 + c*10 + d

Jelas bahawa*1000 + b*100 + c*10 boleh dibahagikan antara 5. Inilah sebabnya kita mempunyai z yang boleh dibahagikan antara 5 jika z - (a*1000 + b*100 + c*10) boleh dibahagikan antara 5.

Tetapi z - (a*1000 + b*100 + c*10) = d dan d adalah nombor angka tunggal, jadi satu -satunya cara untuk dibahagikan antara 5 adalah 0 atau 5.

Oleh itu, z boleh dibahagikan antara 5 jika d = 0 atau d = 5.

Perhatikan bahawa jika z mempunyai n digit demonstrasi adalah sama, ia hanya berubah yang kita sekarang akan menulis z = a₁Ke₂... ke_n Dan objektifnya adalah untuk membuktikannya_n adalah sifar atau lima.

Partition

Kami mengatakan bahawa pemisahan integer positif adalah cara di mana kita dapat menulis nombor sebagai jumlah bilangan bulat positif.

Boleh melayani anda: Radio konvergensi: definisi, contoh dan latihan yang diselesaikan

Perbezaan antara penguraian tambahan dan partition adalah, sementara pada yang pertama ia dicari sekurang -kurangnya ia dapat dipecahkan kepada dua atau lebih, dalam partisi sekatan ini.

Oleh itu, kita mempunyai perkara berikut:

5 = 5

5 = 1+4

5 = 2+3

5 = 1+2+2

Di atas adalah partisi 5.

Iaitu, kita mempunyai semua penguraian tambahan adalah partition, tetapi tidak semua partition semestinya penguraian tambahan.

Dalam Teori Bilangan, teorem asas aritmetik menjamin bahawa setiap nombor boleh ditulis secara unik sebagai produk sepupu.

Apabila partisi dikaji, objektifnya adalah untuk menentukan berapa banyak cara integer positif dapat ditulis sebagai jumlah bilangan bulat lain. Oleh itu, kami menentukan fungsi partition seperti yang ditunjukkan di bawah.

Definisi

Fungsi partition p (n) ditakrifkan sebagai bilangan cara di mana integer positif n dapat ditulis sebagai jumlah bilangan bulat positif.

Kembali ke contoh 5, kita perlu:

5 = 5

5 = 1+4

5 = 2+3

5 = 1+1+3

5 = 1+2+2

5 = 1+1+1+2

5 = 1+1+1+1+1

Dengan cara ini, p (5) = 7.

Graf

Kedua -dua partition dan penguraian tambahan nombor n boleh diwakili secara geometri.  Katakan kita mempunyai penguraian aditif n. Dalam penguraian ini, tambahan boleh diperbaiki supaya ahli -ahli jumlahnya diperintahkan dari yang paling sedikit hingga paling besar. Jadi, ia bernilai:

n = a₁ + ke₂ + ke₃ +... + a_r dengan

ke₁ ≤ a₂ ≤ a₃ ≤ ... ≤ a_r.

Kita boleh grafik berkata penguraian seperti berikut: dalam baris pertama kita menandakan a₁-mata, kemudian dalam yang berikut kami menandakan₂-mata, dan sebagainya sehingga sampai_r.

Boleh melayani anda: Ketidaksamaan segitiga: demonstrasi, contoh, latihan yang diselesaikan

Mari kita ambil sebagai contoh nombor 23 dan penguraian seterusnya:

23 = 5 + 4 + 7 + 3 + 1 +3

Kami memesan penguraian ini dan kami ada:

23 = 1 + 3 + 3 + 4+ 5 + 7

Grafiknya yang sepadan:

Begitu juga, jika kita membaca graf ini secara menegak secara mendatar, kita dapat memperoleh penguraian yang mungkin berbeza dari sebelumnya. Dalam contoh 23, yang berikut menonjol:

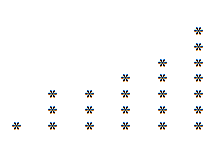
Oleh itu, kita mempunyai 23 bahawa kita juga boleh menulisnya sebagai:

23 = 6 + 5 + 5 + 3 + 2 + 1 + 1.