Simbol diameter dan formula, bagaimana untuk mengeluarkannya, lilitan

Dia diameter Ia adalah garis lurus yang melewati pusat lengkung rata tertutup atau angka dalam dua atau tiga dimensi dan juga menyertai titik bertentangannya. Biasanya bulatan (lengkung rata), bulatan (angka rata), sfera atau silinder bulat lurus (objek tiga dimensi).

Walaupun lilitan dan bulatan biasanya diambil sebagai sinonim, terdapat perbezaan antara kedua -dua istilah. Lingkaran adalah lengkung tertutup yang disertakan ke bulatan, yang memenuhi syarat bahawa jarak antara mana -mana titik dan pusatnya adalah sama. Jarak ini tidak lain daripada jejari lilitan. Sebaliknya, bulatan adalah angka rata yang terhad oleh lilitan.

Rajah 1. Diameter roda basikal adalah ciri penting dalam reka bentuknya. Sumber: Pixabay.

Sekiranya lilitan, bulatan dan sfera, diameternya adalah segmen lurus yang mengandungi sekurang -kurangnya tiga mata: pusat ditambah dua titik dari tepi lilitan atau bulatan, atau permukaan sfera.

Dan bagi silinder bulat lurus, diameter merujuk kepada bahagian silang, yang bersama -sama dengan ketinggian, adalah dua parameter ciri.

Diameter lilitan dan bulatan, yang dilambangkan oleh Ø atau hanya huruf "d" atau "d", berkaitan dengan perimeter, kontur atau panjangnya, yang dilambangkan dengan huruf l:

L = π.D = π. Sama ada

Bila -bila masa anda mempunyai lilitan, kuota antara panjangnya dan diameternya adalah nombor yang tidak rasional π = 3.14159 ..., dengan cara ini:

π = l/d

[TOC]

Cara mendapatkan diameter?

Apabila lukisan lilitan atau bulatan tersedia, atau secara langsung objek bulat, seperti mata wang atau cincin misalnya, sangat mudah untuk mengambil diameter dengan peraturan. Anda hanya perlu memastikan bahawa tepi peraturan pada masa yang sama mempunyai dua titik lilitan dan pusat yang sama.

Boleh melayani anda: algebra

Kaki berkaliber, vernier atau raja sangat sesuai untuk mengukur diameter luaran dan dalaman dalam duit syiling, gelung, cincin, kacang, tiub dan banyak lagi.

Rajah 2. Vernier Digital Mengukur Diameter Koin. Sumber: Pixabay.

Sekiranya bukannya objek atau lukisannya, anda mempunyai data seperti radio R, Kemudian mengalikan dengan 2 anda mempunyai diameter. Dan jika panjang atau perimeter lilitan diketahui, diameter juga dapat diketahui, oleh pelepasan:

D = 2.R
D = l / π

Cara lain untuk mendapatkan diameternya adalah untuk mengetahui kawasan bulatan, permukaan sfera, bahagian silang silinder, kawasan melengkung ini atau jumlah sfera atau silinder. Semuanya bergantung pada angka geometri yang mana. Sebagai contoh, diameter terlibat dalam bidang dan jumlah berikut:

-Kawasan bulatan: π.(D/2)²
-Kawasan permukaan sfera: 4π.(D/2)²
-Jumlah sfera: (4/3) π.(D/2)³
-Jumlah silinder pekeliling lurus: π.(D/2)².H (h ialah ketinggian silinder)

Angka yang tetap lebar

Bulatan adalah tokoh rata yang tetap lebar, kerana di mana sahaja ia kelihatan, lebarnya diameter d. Walau bagaimanapun, terdapat angka lain yang kurang diketahui yang lebarnya juga tetap.

Mula -mula mari kita lihat apa yang difahami dengan lebar angka: ia adalah jarak antara dua garisan selari -support remes -, yang seterusnya berserenjang dengan arah yang diberikan dan yang memenjarakan angka itu, seperti yang ditunjukkan dalam imej kiri:

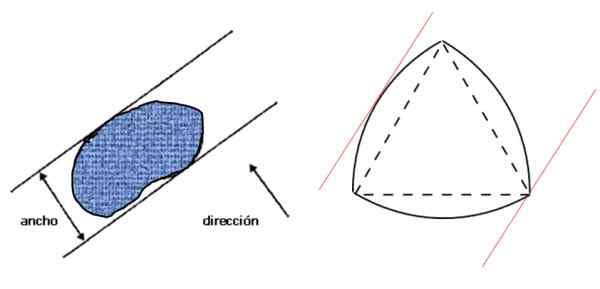Rajah 3. Lebar angka rata (kiri) dan segitiga reuleaux, angka lebar yang tetap (kanan). Sumber: f. Zapata.

Kemudian ke kanan adalah segitiga Reuleaux, yang merupakan angka luas yang tetap dan yang memenuhi syarat yang dinyatakan di angka kiri. Jika lebar angka itu d, perimeternya diberikan oleh teorem Barbier:

Boleh melayani anda: Anggaran pengukuran angka amorf: Contoh dan senaman

L = π.D

Pembetung kota San Francisco di California dibentuk seperti segitiga Reuleaux, yang dinamakan oleh jurutera Jerman Franz Reuleaux (1829 - 1905). Dengan cara ini tapas tidak dapat jatuh ke lubang dan menghabiskan lebih sedikit bahan untuk mengeluarkannya, kerana kawasan mereka kurang daripada bulatan:

A = (1- √3).πd² = 0.705.D²

Sementara untuk bulatan:

A = π.(D/2)² = (π/4) D²= 0.785.D²

Tetapi segitiga ini bukan satu -satunya angka luas yang tetap. Panggilan boleh dibina Poligon Reuleaux dengan poligon lain yang mempunyai nombor sisi ganjil.

Diameter lilitan

Dalam angka seterusnya adalah unsur -unsur lilitan, yang ditakrifkan seperti berikut:

Tali: segmen garis yang menyertai dua titik lilitan. Dalam angka itu adalah tali yang bergabung dengan titik c dan d, tetapi rentetan tak terhingga dapat dikesan yang unik beberapa mata dari lilitan.

Diameter: Ia adalah tali yang melewati pusat, menyertai dua titik lilitan dengan pusat atau. Ia adalah tali terpanjang dari lilitan, kerana sebab itu ia dipanggil "tali utama".

Radio: segmen garis yang bergabung dengan pusat dengan mana -mana titik lilitan. Nilainya, seperti diameter, tetap.

Lilitan: Ini adalah satu set semua mata yang menyamakan atau.

Tunduk: Ia ditakrifkan sebagai segmen lilitan yang dibatasi oleh dua radio (tidak ditarik dalam angka).

Rajah 4. Bahagian lilitan, termasuk diameter, yang melewati pusat. Sumber: Wikimedia Commons.

- Contoh 1

Rectangle yang ditunjukkan berukuran 10 inci tinggi, yang ketika penggulungan ia membentuk silinder bulat lurus yang diameternya adalah 5 inci. Jawab soalan berikut:

Ia boleh melayani anda: Peristiwa yang saling eksklusif: Contoh dan Contohnya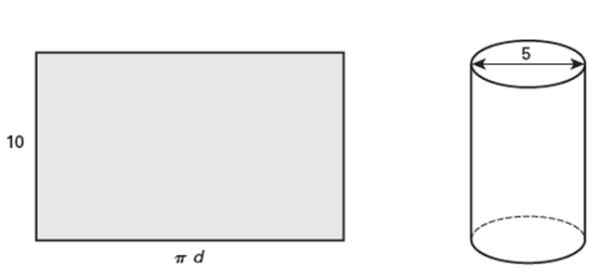Rajah 5. Segi empat tepat bergulir menjadi silinder bulat lurus. Sumber: Jiménez, R. Matematik II. Geometri dan trigonometri. 2. Edisi. Pearson.

a) Apakah kontur tiub?
b) Cari kawasan segi empat tepat
c) Kirakan kawasan cross -section silinder.

Penyelesaian kepada

Kontur tiub adalah l = π.D = 5π PLG = 15.71 plg.

Penyelesaian b

Kawasan segi empat tepat adalah Asas x ketinggian, menjadi asas l sudah dikira dan ketinggian adalah 10 PLG mengikut pernyataan, oleh itu:

A = 15.71 PLG x 10 PLG = 157.1 plg².

Penyelesaian c

Akhirnya, kawasan yang diminta dikira seperti berikut:

A = π.(D/2)² = (π/4) D² = (π/4) x (5 PLG)²= 19.63 plg².

- Contoh 2

Kirakan kawasan berlorek Rajah 5a. Dataran mempunyai sisi l.

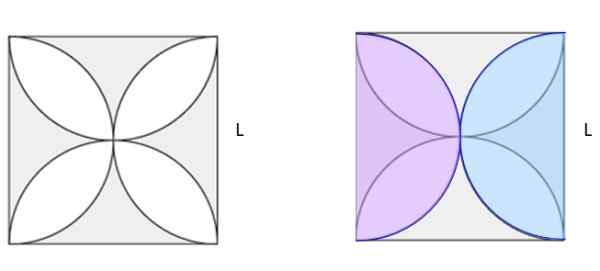Rajah 6. Cari kawasan yang berlorek di angka kiri. Jiménez, r. Matematik II. Geometri dan trigonometri. 2. Edisi. Pearson.

Penyelesaian

Dalam Rajah 5b, dua saiz separuh bulatan yang sama dalam warna merah jambu dan biru telah ditarik, ditumpukan pada angka asal. Di antara mereka mereka membuat bulatan lengkap. Jika kuadrat dataran dikira dan kawasan bulatan dikurangkan, ia menjadikan kawasan berlorek Rajah 5b. Dan kelihatan baik, ternyata separuh daripada kawasan teduh di 5A.

-Dataran Kawasan: l²
-Diameter separuh bulatan: l
-Kawasan bulatan: π.(L/2)²= (π/4) l²
-Perbezaan kawasan = separuh kawasan berlorek =

L² - (π/4) l² = [(4 - π)/4] l²= 0.2146 l²

-Kawasan teduh = 2 x 0.2146 l²= 0.4292L2

Berapa banyak diameter yang mempunyai lilitan?

Diameter tak terhingga boleh ditarik dalam bulatan, dan mana -mana daripada mereka mengukur sama.

Rujukan

1. Antonio. Segitiga reuleaux dan lengkung lebar tetap lain. Pulih dari: penyebaran.com.
2. Baldor, a. 2002. Geometri rata dan ruang dan trigonometri. Kumpulan tanah air budaya.
3. Jiménez, r. Matematik II. Geometri dan trigonometri. 2. Edisi. Pearson.
4. Wikipedia. Segitiga Reuleaux. Pulih dari: ia adalah.Wikipedia.org.
5. Wolfram Mathworld. Diameter. Pulih dari: Mathworld.Wolfram.com.