Dinamik contoh sistem zarah, latihan

The Dinamik sistem zarah Ia terdiri daripada penerapan undang -undang Newton dari pergerakan ke satu set zarah, yang boleh menjadi bijak (zarah boleh dikira) atau menjadi sebahagian daripada objek yang dilanjutkan, dalam hal ini sistem berterusan.

Untuk menerangkan pergerakan sistem zarah, sukar untuk menganalisis masing -masing secara berasingan dan melihat apa daya bertindak di atasnya. Sebaliknya, titik wakil set ditakrifkan, dipanggil Pusat Massa.

Menggambarkan Pergerakan Pusat Massa menawarkan panorama yang sangat berjaya dalam pergerakan global set, juga membolehkan untuk memohon undang -undang Newton yang sama dengan apabila objek dianggap sebagai zarah tanpa dimensi.

Model terakhir ini, yang dipanggil Model zarah, Adalah baik untuk menggambarkan terjemahan dan juga apabila tidak perlu mempertimbangkan dimensi objek. Tetapi objek biasa adalah saiz dan jika mereka juga mempunyai pergerakan putaran, perlu mengambil kira titik -titik di mana daya digunakan.

[TOC]

Contoh

Bumi dan bulan

Ilustrasi bumi dan bulan

Satu set zarah diskret m₁, m₂, m₃... yang akhirnya bergerak berkenaan dengan asal -usul sistem koordinat, disebabkan oleh beberapa daya yang dihasilkan yang bertindak ke atasnya adalah contoh sistem zarah yang baik.

Bumi boleh dianggap sebagai satu zarah dan bulan yang lain, maka kedua -duanya merupakan sistem 2 zarah di bawah tindakan kekuatan graviti matahari.

Objek lanjutan

Seseorang, haiwan atau mana -mana objek persekitaran, juga boleh dianggap sebagai sistem zarah, hanya bahawa ini sangat kecil, yang tidak dapat mengira satu demi satu. Ini adalah sistem yang berterusan, tetapi dengan mengambil kira pertimbangan tertentu, rawatannya adalah sama seperti sistem yang bijak.

Ia dapat melayani anda: apakah entalpi latihan? (Dengan latihan)

Inilah perinciannya.

Pusat massa sistem zarah

Untuk memulakan kajian sistem zarah, anda perlu mencari pusat jisim (cm), yang merupakan titik di mana keseluruhan jisim sistem tertumpu.

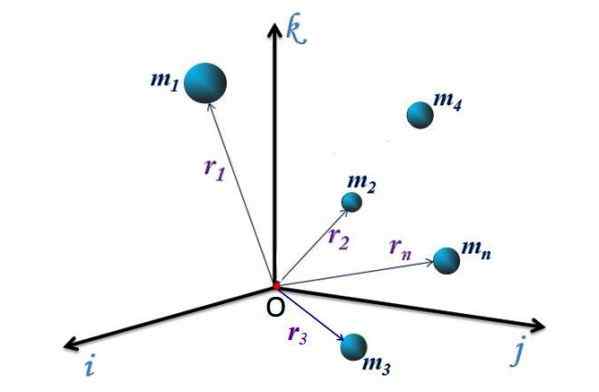
Rajah 1. Sistem zarah dalam sistem rujukan XYZ. Sumber: f. Zapata.

Untuk sistem diskret Rajah 1, dengan n zarah, masing -masing mempunyai vektor kedudukan yang diarahkan dari sistem asal atau koordinat ke titik p (x, y, z) di mana zarahnya. Vektor ini dilambangkan sebagai r₁, r₂, r₃… r_n.

Koordinat CM dikira dengan persamaan berikut:

Di mana setiap massa set diwakili sebagai m₁, m₂, m₃... m_n. Perhatikan bahawa jumlah Σ m_Yo Ia bersamaan dengan jumlah jisim m set. Sekiranya sistem berterusan, ringkasan digantikan dengan integral.

Setiap alamat tegak lurus diwakili oleh vektor unit Yo, J dan k, Oleh itu, vektor kedudukan CM, dilambangkan r_Cm, Ia boleh dinyatakan oleh:

r_Cm = x_Cm Yo + dan_Cm J + z_Cm k

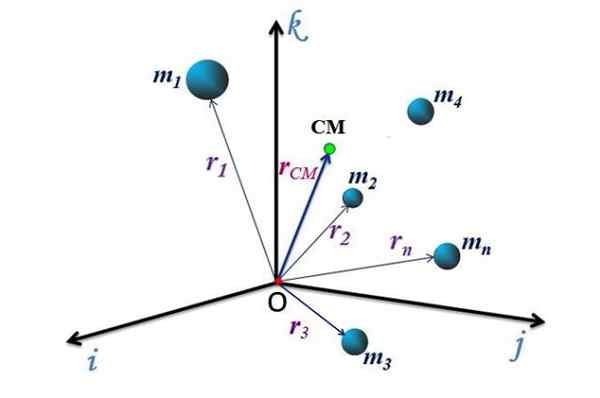Rajah 2. Lokasi pusat massa sistem zarah. Sumber: f. Zapata.

Pergerakan CM

Setelah lokasi pusat jisim diketahui, persamaan pergerakan yang diketahui digunakan. Kelajuan CM adalah yang pertama yang diperoleh dari kedudukan berkenaan dengan masa:

Dalam kes ini, sistem ini mempunyai jumlah pergerakan P yang dikira sebagai hasil daripada jumlah jisim sistem dan kelajuan pusat jisim:

Ia boleh melayani anda: trajektori fizikal: ciri, jenis, contoh dan latihan

P = M ∙v_Cm

Sebagai alternatif, jumlah sistem sistem boleh dikira secara langsung:

P = m₁v₁ + m₂v₂ + m₃v₃ +… . = Σ m_Yo v_Yo

Walaupun pecutan cm adalah kelajuan yang diperolehi:

Kekuatan pada cm

Daya yang bertindak pada sistem zarah boleh:

• Daya dalaman, disebabkan oleh interaksi antara zarah yang sama.
• Daya luaran, disebabkan oleh ejen yang luaran ke sistem.

Oleh kerana daya dalaman dibentangkan oleh pasangan, magnitud dan arah yang sama, tetapi deria yang bertentangan, menurut undang -undang ketiga Newton, ia dipenuhi bahawa:

Σ F_int = 0

Oleh itu, daya dalaman tidak mengubah pergerakan keseluruhannya, tetapi mereka sangat penting untuk menentukan tenaga dalaman.

Sekiranya sistem itu terpencil dan tidak ada daya luaran, menurut undang -undang pertama Newton, pusat massa berehat atau bergerak dengan pergerakan rectilinear seragam. Jika tidak, pusat pengalaman massa percepatan yang diberikan oleh:

Σ F_ext = M ∙ke_Cm

Di mana m adalah jumlah jisim sistem. Persamaan sebelumnya boleh ditulis seperti ini:

Dan ini bermaksud bahawa kekuatan luaran bersamaan dengan variasi sementara dalam jumlah pergerakan, cara lain untuk menyatakan undang -undang kedua Newton dan yang sama digunakan oleh ahli fizik Inggeris yang terkenal dalam bukunya Prinsip.

Latihan diselesaikan

Pusat massa sistem zarah 2 berada pada paksi x pada saat tertentu, dalam kedudukan x = 2.0 m dan bergerak dengan kelajuan 5.0 m/s ke arah yang sama dan positif. Sekiranya salah satu zarah adalah asal dan yang lain, jisim 0.1 kg, berehat di x = 8.0 m, hitung:

Boleh melayani anda: Diamagnetism: Bahan, Aplikasi, Contoh

a) jisim zarah yang berasal dari asal.

b) Jumlah pergerakan sistem

c) kelajuan apakah zarah yang ada di asalnya?

Penyelesaian kepada

Dari persamaan untuk kedudukan pusat jisim:

r_Cm = x_Cm Yo + dan_Cm J + z_Cm K = 2.0 m Yo

Oleh kerana CM mempunyai koordinat X sahaja, persamaan trio pertama yang diberikan sebelum ini digunakan:

Koordinat kini diganti, jika zarah dilambangkan pada asal seperti nombor 1 dan yang lain seperti nombor 2, data berangka adalah:

x₁ = 0 m, x₂ = 8.0 m, m₂ = 0.1 kg, x_Cm = 2.0 m

Menginap:

= 0.3kg

Penyelesaian b

Jumlah pergerakan sistem dikira oleh:

P = M ∙v_Cm

Jumlah jisim m adalah sama dengan:

M = 0.3 kg + 0.1 kg = 0.4 kg

Oleh itu:

P = 0.4 kg ∙ 5.0 m/s Yo = 2 kg.Cik Yo

Penyelesaian c

Persamaan untuk P dari sistem dua bahagian, ia membersihkan v₁, Oleh kerana data lain diketahui, kerana pernyataan itu mengatakan bahawa zarah 2 berada di tempat rehat, oleh itu:

v₂ = 0 

Dan P Ia seperti:

P = m₁v₁

v₁ = P / m₁ = 2 kg.Cik Yo / 0.3kg = 6.67 m/s Yo

Rujukan

1. Duke University. Sistem zarah. Pulih dari: webhome.Phy.Duke.Edu.
2. Rex, a. 2011. Asas Fizik. Pearson.
3. Sears, Zemansky. 2016. Fizik universiti dengan fizik moden. Ke -14. Ed. Jilid 1. Pearson.
4. Serway, r., Jewett, J. (2008). Fizik untuk Sains dan Kejuruteraan. Jilid 1. Ke -7. Ed. Pembelajaran Cengage.
5. Tipler, ms. (2006) Fizik untuk Sains dan Teknologi. Edisi ke -5. Jilid 1. Editorial kembali.