Pengagihan formula biasa, ciri, contoh, senaman

The taburan normal O Gaussian Distributi.

Nama pengedaran biasa berasal dari fakta bahawa pengedaran ini adalah yang digunakan untuk bilangan situasi terbesar di mana beberapa pemboleh ubah rawak berterusan terlibat dalam kumpulan atau penduduk tertentu.

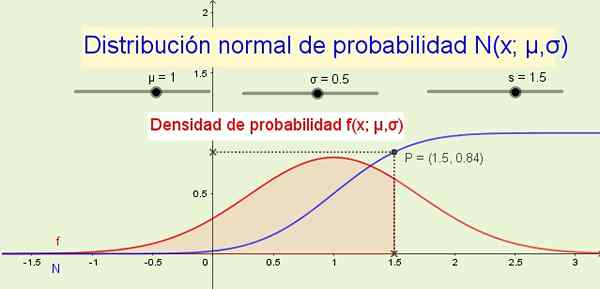
Rajah 1. Pengedaran normal n (x; μ, σ) dan ketumpatan kebarangkalian F (s; μ, σ). (Huraian sendiri)

Sebagai contoh di mana pengedaran normal digunakan: ketinggian lelaki atau wanita, variasi sejauh mana beberapa magnitud fizikal atau dalam ciri -ciri psikologi atau sosiologi yang boleh diukur seperti kota intelektual atau tabiat penggunaan produk tertentu.

Sebaliknya, ia dipanggil pengedaran Gaussian atau Gauss Bell, kerana ia adalah jenius matematik Jerman yang dikreditkan dengan penemuannya untuk kegunaan yang diberikannya untuk perihalan kesilapan statistik pengukuran astronomi pada tahun 1800.

Walau bagaimanapun, ia mendakwa bahawa pengedaran statistik ini sebelum ini diterbitkan oleh ahli matematik yang hebat dari asal Perancis, seperti Abraham de Moivre, kembali pada tahun 1733.

[TOC]

Formula

Ke fungsi pengedaran normal dalam pemboleh ubah berterusan x, Dengan parameter μ dan σ Ia dilambangkan oleh:

N (x; μ, σ)

Dan secara eksplisit ia ditulis seperti ini:

N (x; μ, σ) = ∫_-∞^x F (s; μ, σ) ds

di mana f (u; μ, σ) Ia adalah fungsi ketumpatan kebarangkalian:

f (s; μ, σ) = (1/(σ√ (2π)) exp ( - s²/(2σ²)

Pemalar yang mengalikan fungsi eksponen dalam fungsi ketumpatan kebarangkalian dipanggil pemalar normalisasi, dan telah dipilih sedemikian rupa sehingga:

N (+∞, μ, σ) = 1

Ungkapan sebelumnya memastikan kebarangkalian pembolehubah rawak x antara -∞ dan +∞ sama ada 1, iaitu 100% kebarangkalian.

Parameter μ Ia adalah min aritmetik pemboleh ubah rawak berterusan x dan σ Sisihan piawai atau akar kuadrat dari varians pembolehubah yang sama. Sekiranya berlaku itu μ = 0 dan σ = 1 Anda mempunyai taburan pengedaran standard atau normal biasa: 

N (x; μ = 0, σ = 1)

Ciri -ciri pengedaran normal

1- Jika pemboleh ubah statistik rawak mengikuti taburan ketumpatan kebarangkalian normal F (s; μ, σ), Sebilangan besar data dikumpulkan sekitar nilai purata μ Dan mereka tersebar di sekelilingnya sehingga hanya di antara data μ - σ dan μ + σ. 

Boleh melayani anda: kekerapan mutlak: formula, pengiraan, pengedaran, contoh

2- sisihan piawai σ Ia sentiasa positif.

3- Bentuk fungsi ketumpatan F Ia menyerupai loceng, jadi fungsi ini sering dipanggil Bell Gaussian atau fungsi Gaussian. 

4- Dalam pengedaran Gaussian purata, median dan fesyen bertepatan.

5- Titik infleksi fungsi ketumpatan kebarangkalian didapati tepat di μ - σ dan μ + σ.

6- Fungsi F adalah simetri berkenaan dengan paksi yang dilalui oleh nilai purata μ Dan anda mempunyai sifar asymptotically untuk x ⟶ +∞ dan x ⟶ -∞.

7- nilai yang lebih tinggi daripada σ penyebaran, bunyi bising atau menjauhkan data yang lebih besar di sekitar nilai purata. Itu adalah lebih besar σ Bentuk loceng lebih terbuka. Sebaliknya σ Kecil menunjukkan bahawa dadu berenang ke purata dan bentuk loceng lebih tertutup atau menunjuk.

8- Fungsi Pengedaran N (x; μ, σ) menunjukkan kebarangkalian bahawa pemboleh ubah rawak kurang dari atau sama dengan x. Contohnya, dalam Rajah 1 (di atas) kebarangkalian p bahawa pembolehubah x kurang dari atau sama dengan 1.5 adalah 84% dan sepadan dengan kawasan di bawah fungsi ketumpatan kebarangkalian F (x; μ, σ) Dari -∞ ke x.

Selang amanah

9- Jika data mengikuti taburan normal, maka 68.26% daripadanya adalah antara μ - σ dan μ + σ.

10-95.44% daripada data yang mengikuti taburan normal adalah antara μ - 2σ dan μ + 2σ.

11-99.74% daripada data yang mengikuti taburan normal adalah antara μ - 3σ dan μ + 3σ.

12- Sekiranya pemboleh ubah rawak x Ikuti pengedaran N (x; μ, σ), Maka pembolehubah

Z = (x - μ) / σ  Ikuti taburan normal standard  N (z; 0.1).

Perubahan pembolehubah x kepada z Ia dipanggil penyeragaman atau tipikal dan sangat berguna pada masa menggunakan jadual pengedaran standard ke data yang mengikuti taburan bukan standard biasa.

Aplikasi pengedaran normal

Untuk memohon pengagihan normal, perlu melalui pengiraan integral ketumpatan kebarangkalian, yang dari sudut pandang analisis tidak mudah dan tidak selalu tersedia program komputer yang membolehkan pengiraan berangka. Untuk tujuan ini, jadual nilai standard atau ditandakan digunakan, yang tidak lebih daripada taburan normal dalam kes itu μ = 0 dan σ = 1.

Boleh melayani anda: Operasi gabungan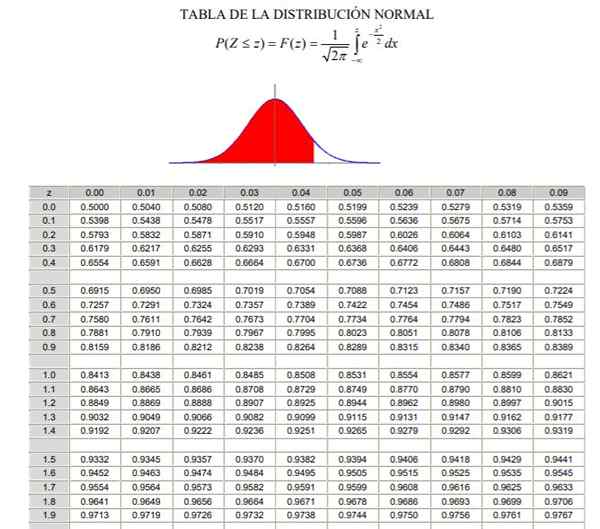Jadual Pengagihan Normal (Bahagian 1/2) 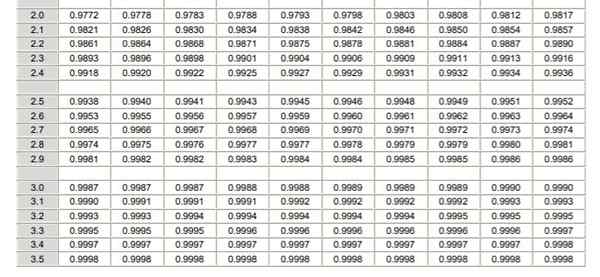Jadual Pengagihan Normal (Bahagian 2/2)

Harus diperhatikan bahawa jadual ini tidak termasuk nilai negatif. Walau bagaimanapun, menggunakan sifat simetri fungsi ketumpatan kebarangkalian Gaussian, nilai yang sepadan dapat diperoleh. Dalam latihan yang diselesaikan yang ditunjukkan di bawah penggunaan jadual ditunjukkan dalam kes ini.

Contoh

Anggapkan bahawa anda mempunyai set data rawak x yang mengikuti pengedaran purata normal 10 dan sisihan piawai 2. Diminta untuk mencari kebarangkalian bahawa:

a) Pembolehubah rawak x kurang daripada atau sama dengan 8.

b) kurang daripada atau sama dengan 10.

c) Pembolehubah X adalah di bawah 12.

d) Kebarangkalian nilai x antara 8 dan 12.

Penyelesaian:

a) Untuk menjawab soalan pertama yang anda hanya perlu mengira:

N (x; μ, σ)

Dengan x = 8, μ = 10 dan σ = 2. Kami menyedari bahawa ia adalah integral yang tidak mempunyai penyelesaian analisis dalam fungsi asas, tetapi penyelesaiannya dinyatakan mengikut fungsi ralat Erf (x).

Sebaliknya, terdapat kemungkinan menyelesaikan integral dengan cara berangka, iaitu banyak kalkulator, spreadsheet dan program komputer seperti geogebra lakukan. Angka berikut menunjukkan penyelesaian berangka yang sepadan dengan kes pertama:

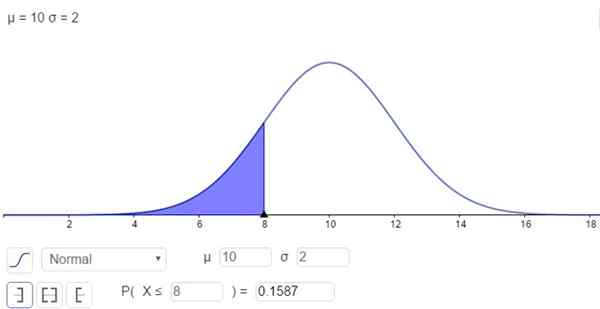Rajah 2. Ketumpatan kebarangkalian F (x; μ, σ). Kawasan berlorek mewakili p (x ≤ 8). (Huraian sendiri)

Dan jawapannya ialah kebarangkalian bahawa x di bawah 8 adalah:

P (x ≤ 8) = n (x = 8; μ = 10, σ = 2) = 0.1587

b) Dalam kes ini, tentang mencari kebarangkalian bahawa pembolehubah rawak x berada di bawah purata yang dalam kes ini bernilai 10. Jawapannya tidak memerlukan pengiraan, kerana kita tahu bahawa separuh daripada data berada di bawah purata dan separuh lagi di atas purata. Oleh itu, jawapannya ialah:

P (x ≤ 10) = n (x = 10; μ = 10, σ = 2) = 0.5

c) Untuk menjawab soalan ini, anda harus mengira N (x = 12; μ = 10, σ = 2), yang boleh dilakukan dengan kalkulator yang mempunyai fungsi statistik atau perisian seperti geogebra:

Boleh melayani anda: Pembahagi 8: Apa dan Penjelasan Mudah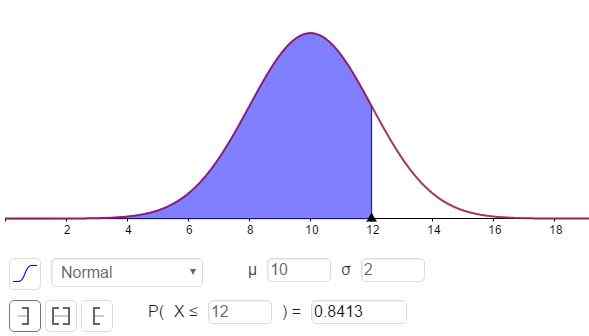Rajah 3. Ketumpatan kebarangkalian F (x; μ, σ). Kawasan berlorek mewakili p (x ≤ 12). (Huraian sendiri)

Tanggapan kepada Bahagian C dapat dilihat dalam Rajah 3 dan adalah:

P (x ≤ 12) = n (x = 12; μ = 10, σ = 2) = 0.8413.

d) Untuk mencari kebarangkalian bahawa pembolehubah rawak x adalah antara 8 dan 12 kita boleh menggunakan hasil bahagian a dan c seperti berikut:

P (8 ≤ x ≤ 12) = p (x ≤ 12) - P (x ≤ 8) = 0.8413 - 0.1587 = 0.6826 = 68.26.

Latihan diselesaikan

Harga purata saham syarikat ialah $ 25 dengan sisihan piawai $ 4. Tentukan kebarangkalian bahawa:

a) Tindakan mempunyai kos kurang dari $ 20.

b) yang mempunyai kos lebih besar daripada $ 30.

c) Harga antara $ 20 dan $ 30.

Gunakan jadual pengedaran normal yang ditandai untuk mencari jawapan.

Penyelesaian:

Untuk menggunakan jadual, perlu bergerak ke pemboleh ubah yang dinormalisasi atau ditandatangani:

$ 20 dalam pemboleh ubah piawai sama dengan z = ($ 20 - $ 25) / $ 4 = -5/4 = -1,25 dan 

$ 30 dalam pemboleh ubah piawai sama dengan z = ($ 30 - $ 25) / $ 4 = +5/4 = +1.25.

a) $ 20 bersamaan dengan -1,25 dalam pemboleh ubah piawai, tetapi jadual tidak mempunyai nilai negatif, jadi kami meletakkan nilai +1.25 yang menunjukkan nilai 0.8944.

Jika nilai ini dikurangkan 0.5 hasilnya akan menjadi kawasan antara 0 dan 1.25 yang, dengan cara itu, adalah sama (oleh simetri) ke kawasan antara -1.25 dan 0. Hasil penolakan ialah 0.8944 - 0.5 = 0.3944 yang merupakan kawasan antara -1.25 dan 0.

Tetapi kepentingan kawasan dari -∞ hingga -1,25 yang akan menjadi 0.5 -0.3944 = 0.1056. Oleh itu, disimpulkan bahawa kebarangkalian tindakan di bawah $ 20 adalah 10.56%.

b) $ 30 dalam pemboleh ubah yang ditandatangani z ialah 1.25. Untuk nilai ini dalam jadual muncul nombor 0.8944 yang sepadan dengan kawasan dari -∞ hingga +1.25. Kawasan antara +1.25 y +∞ ialah (1 - 0.8944) = 0.1056. Dengan kata lain, kebarangkalian bahawa tindakan kos lebih daripada $ 30 adalah 10.56%.

c) Kebarangkalian bahawa tindakan mempunyai kos antara $ 20 dan $ 30 akan dikira seperti berikut:

100% -10.56% - 10.56% = 78.88%

Rujukan

1. Statistik dan kebarangkalian. Taburan normal. Diperolehi daripada: ProjectodeScartes.org
2. Geogebra. Geogebra klasik, pengiraan kebarangkalian. Pulih dari geogebra.org
3. Mathworks. Pengagihan Gauss. Pulih dari: Adakah.Mathworks.com
4. Mendenhall, w. 1981. Statistik untuk Pentadbiran dan Ekonomi. Ke -3. edisi. Kumpulan Editorial Iberoamerica.
5. Stat Trek. Ajarkan diri anda statistik. Pengagihan Poisson. Pulih dari: stattrek.com,
6. Triola, m. 2012. Statistik asas. 11hb. Ed. Pendidikan Pearson.
7. Universiti Vigo. Pengagihan berterusan utama. Pulih dari: ANAPG.laman web.Uvigo.adalah
8. Wikipedia. Taburan normal. Pulih dari: Adakah.Wikipedia.org