Pengagihan seragam berterusan ciri, contoh, aplikasi
- 1490
- 177
- Clarence Greenholt DDS
Pemboleh ubah rawak mempunyai a Pengagihan seragam yang berterusan Sekiranya kebarangkalian mengambil nilai, dalam selang terhingga [a, b], adalah sama untuk mana-mana sub-interval yang sama panjang.
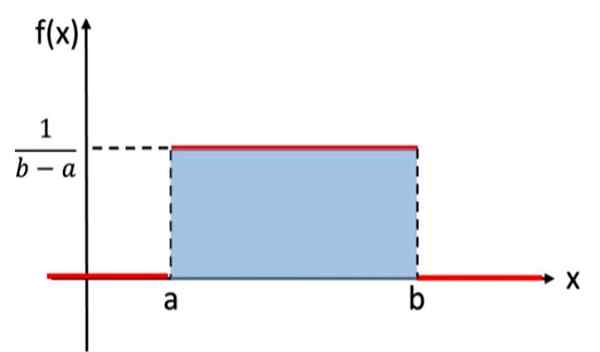
Pengagihan ini sama dengan taburan seragam diskret, yang diberikan kepada setiap hasil eksperimen rawak kebarangkalian yang sama, tetapi dalam hal ini pembolehubah yang akan dipertimbangkan adalah berterusan. Sebagai contoh, eksperimen yang terdiri daripada memilih nombor sebenar rawak, antara nilai a dan b, mengikuti taburan seragam. Di sini anda mempunyai graf anda:
Rajah 1. Graf fungsi ketumpatan taburan seragam yang berterusan Dalam notasi matematik, pengedaran seragam berterusan mempunyai fungsi ketumpatan yang ditakrifkan sebagai fungsi kepada kepingan atau oleh bahagian, yang boleh ditulis sebagai:
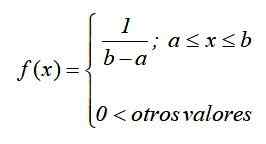
Graf fungsi ini, yang dikenali sebagai Fungsi lengkung atau ketumpatan, Ia adalah segi empat tepat, jadi taburan seragam berterusan juga dikenali sebagai pengedaran segi empat tepat Dan ia adalah yang paling mudah dari pengagihan berterusan.
Kawasan di bawah graf pengagihan kebarangkalian adalah sama dengan 1 dan selalu mengambil nilai positif. Pengagihan seragam memenuhi kriteria ini. Tidak perlu mengintegrasikan secara langsung untuk mengesahkan bahawa kawasan itu adalah 1, kerana kawasan segi empat tepat di Rajah 1 dapat dikira menggunakan formula:
Kawasan = asas x ketinggian = (b - a) x [1/(b - a)] = 1
Mengetahui kawasan di bawah lengkung ketumpatan sangat penting, kerana terdapat hubungan antara kawasan dan kebarangkalian kejadian kejadian, yang untuk pengedaran ini ditentukan dalam bahagian berikut.
Ciri -ciri pengedaran seragam yang berterusan
Pengagihan seragam berterusan dicirikan olehnya:
Fungsi ketumpatan
Biarkan x menjadi pemboleh ubah rawak yang berterusan, yang tergolong dalam selang [a, b], kemudian:
Ia boleh melayani anda: transformasi linear: sifat, apakah penggunaan, jenis, contoh=\frac1b-a)
Fungsi pengedaran
Dengan menggunakan fungsi pengedaran, kebarangkalian pembolehubah rawak x mengambil nilai x dari nilai yang mungkin dari selang [a, b] dikira. Untuk pengedaran berterusan, ia biasanya dikira dengan cara ini:
=\int_a^xf(x)dx)
Dalam kes taburan seragam yang berterusan, kebarangkalian f (x) bersamaan dengan kawasan segi empat tepat yang asasnya (X-A) dan ketinggiannya (B-A):
=\int_a^x\left&space;(\frac1b-a&space;\right&space;)dx=\fracx-ab-a)
Secara matematik, jika f (x) = pr (x = x) fungsi berikut ditubuhkan oleh bahagian, mengikut hasil sebelumnya:
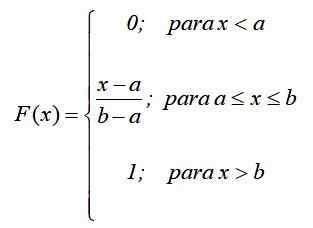
Dengan cara ini, apa yang telah dikatakan sebelum ini: kebarangkalian hanya bergantung pada nilai (x-a) dan bukan di lokasinya dalam selang waktu [a, b]. Grafik fungsi pengedaran adalah:
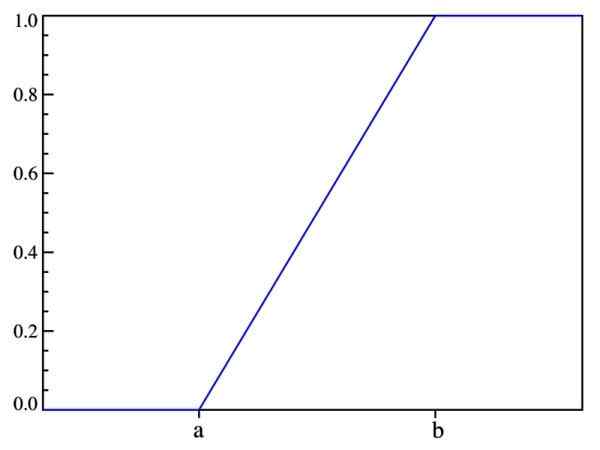Rajah 2. Graf fungsi pengedaran f (x). Sumber: Wikimedia Commons. Nilai yang diharapkan, varians dan sisihan piawai
Setelah melakukan banyak eksperimen dengan pemboleh ubah rawak yang berterusan, nilai purata dipanggil nilai yang dijangkakan, Ia dilambangkan sebagai E (x) dan dikira oleh integral berikut:
=\int_a^bxf(x)=\int_a^b\left&space;(\frac1b-a&space;\right&space;)xdx=\left&space;(\frac1b-a&space;\right&space;)\frac(b^2-a^2)2=\fraca+b2)
V (x) = e (x2) - Ex)2
Oleh itu:
=\left&space;[\int_a^bx^2f(x)dx&space;\right&space;]-\left&space;(\fraca+b2&space;\right&space;)^2=\left&space;[\int_a^bx^2\left&space;(\fracb-a2&space;\right&space;)&space;dx\right&space;]-\left&space;(\fraca+b2&space;\right&space;)^2)
=\frac(b-a)^212)
D (x) = √ V (x)
=\sqrt\frac(b-a)^212)
Median, fesyen, simetri dan curtosis
Ia dapat dengan mudah disahkan bahawa median, yang merupakan nilai pusat pengedaran seragam, adalah sama dengan purata, dan kerana tidak ada nilai yang diulangi lebih daripada yang lain, kerana semuanya sama mungkin dalam selang waktu [a, b ], fesyen tidak wujud.
Bagi simetri, taburan seragam adalah simetri dan curtosis, yang merupakan sejauh mana nilai -nilai di sekitar pusat tertumpu ialah -6/5.
Boleh melayani anda: Apakah 7 elemen lilitan?Contoh
Pelbagai situasi boleh dimodelkan melalui pengedaran berterusan, dan dengan itu meramalkan tingkah laku mereka. Berikut adalah beberapa contoh:
Contoh 1
Sebuah syarikat yang menyediakan perkhidmatan elektrik menyediakan tahap voltan yang diedarkan secara merata, antara 123.0 V dan 125.0 v. Ini bermakna bahawa dalam pukulan domestik adalah mungkin untuk mendapatkan apa -apa nilai voltan yang dimiliki oleh selang waktu itu.
Kemudian, seperti yang dilihat di atas, graf fungsi ketumpatan adalah segi empat tepat merah:
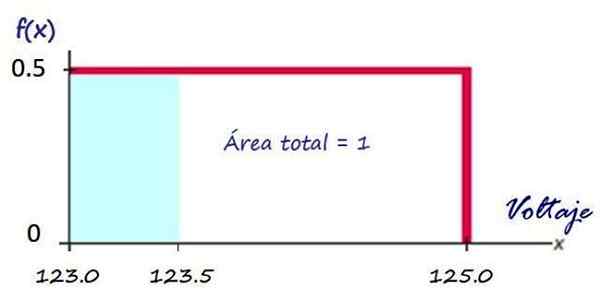Rajah 3. Fungsi ketumpatan untuk voltan yang disampaikan oleh syarikat elektrik. Sumber: f. Zapata. Mengira kebarangkalian mempunyai voltan dalam selang waktu yang diberikan sangat mudah, sebagai contoh, apakah kebarangkalian syarikat akan menghantar voltan kurang dari 123.5 v?
Kebarangkalian ini bersamaan dengan kawasan segi empat tepat yang berlorek dalam warna biru:
P (x<123.5) = (123.5 −123.0)x 0.5 = 0.25
Dan apakah kebarangkalian bahawa voltan yang disampaikan lebih besar daripada 124.0 v?
Oleh kerana jumlah kawasan adalah sama dengan 1, kebarangkalian yang dicari adalah:
P (x> 124.0 v) = 1 - (1 × 0.5) = 0.5
Masuk akal, sejak 124.0 adalah tepat nilai di tengah selang waktu.
Contoh 2
Pembolehubah rawak tertentu x mempunyai taburan seragam dalam selang [0.100]. Tentukan:
a) Kebarangkalian bahawa nilai x kurang dari 22.
b) Kebarangkalian bahawa x mengambil nilai antara 20 dan 35.
c) nilai yang diharapkan, varians dan sisihan piawai pengedaran ini.
Jawapan kepada
Ia ditentukan sama dengan contoh sebelumnya, tetapi pertama -tama kita mesti menentukan ketinggian segi empat tepat, mengingati bahawa jumlah kawasan mestilah sama dengan 1:
Kawasan = 100 × ketinggian = 1
Oleh itu segi empat tepat mempunyai ketinggian yang sama dengan 1/100 = 0.01
Boleh melayani anda: Decagon: biasa, tidak teratur, sifat, contohP (x<22) = 22×0.01 = 0.22
Jawab b
Kebarangkalian yang diminta bersamaan dengan kawasan segi empat tepat yang lebarnya (35 - 20) dan ketinggiannya 0.01:
P (22 Jika anda lebih suka pergi terus ke fungsi pengedaran di atas, maka anda hanya perlu menggantikan nilai dalam: P (20≤x≤35) = F (35) -f (20) Dengan f (x) yang diberikan oleh: F (x) = (x-a) / (b-a) Nilai yang akan diperkenalkan ialah: A = 0 B = 100 F (35) = (35-0) / (100-0) = 0.35 F (20) = (20-0) / (100-0) = 0.dua puluh P (20≤x≤35) = 0.35-0.20 = 0.lima belas Nilai yang diharapkan ialah: E (x) = (a+b)/2 = (100+0)/2 = 50 Variansnya ialah: V (x) = (b-a)2/12 = (100-0)2/12 = 833.33 Dan sisihan piawai adalah: D (x) = √833.33 = 28.87 Pengagihan ini berguna apabila proses simulasi statistik dijalankan atau ketika bekerja pada peristiwa yang kekerapan penampilannya biasa. Beberapa bahasa pengaturcaraan menjana nombor rawak antara 0 dan 1, dan seperti yang dapat dilihat dari contoh sebelumnya, pengedaran kebarangkalian diikuti adalah seragam. Dalam kes ini selang untuk dipertimbangkan ialah [0.1]. Sekiranya anda mempunyai percubaan di mana peristiwa mempunyai keteraturan, seperti yang dijelaskan di atas, anda boleh, pada dasarnya, berikan kepada setiap kebarangkalian yang sama kejadian. Dalam kes ini, model probabilistik pengedaran seragam memberikan maklumat untuk analisis. Pengagihan seragam juga digunakan dalam pembulatan perbezaan antara nilai yang diperhatikan dan nilai sebenar pembolehubah, dengan mengandaikan pengagihan seragam kesilapan dalam selang tertentu, menurut pembulatan, biasanya -0.5 hingga +0.5.Jawab c
Aplikasi
Nombor rawak
Pensampelan pengedaran sewenang -wenang
Ralat pembulatan
Rujukan