Persamaan Clausius-Clapeyron Apa itu, Contoh, Latihan

The Persamaan Clausius-Clapeyron Ia adalah salah satu yang berkaitan dengan perubahan tekanan wap dan suhu, dalam fasa atau perubahan peralihan keadaan. Terpakai untuk sublimasi, penguap, penggabungan, atau bahkan dalam perubahan dalam fasa kristal. Perlu dinyatakan bahawa persamaan ini terpakai kepada bahan tulen yang ada dalam keseimbangan.

Persamaan ini berasal dari undang-undang termodinamik dan gambar rajah P-T untuk bahan, di mana garis kewujudan bersama diperhatikan; yang memisahkan dua fasa yang berbeza (cecair-wap, pepejal-cecair, dll.). Untuk memindahkan garis ini, keuntungan atau kehilangan haba diperlukan, seperti entalpi pengewapan, ΔH_Vap.

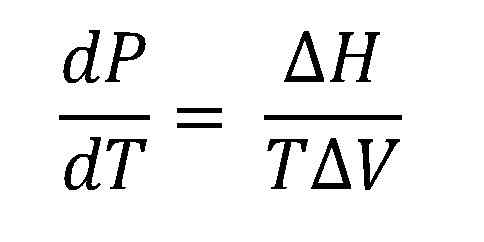Persamaan Clausius-Clapeyron. Sumber: Gabriel Bolívar.

Imej yang lebih tinggi menunjukkan persamaan Clausius-Clapeyron sebelum disepadukan. Biasanya ia biasanya digunakan untuk sistem wap cecair, di mana ΔH digunakan_Vap dan anda ingin mengira apa tekanan wap cecair pada suhu tertentu. Ia juga berfungsi untuk mengira ΔH_Vap cecair tertentu dalam julat suhu.

Persamaan Clausisu-Clapeyron juga digunakan dengan kerap untuk mengkaji perubahan tekanan dalam pepejal yang tidak menentu; iaitu, entalpi sublimasi dipertimbangkan, ΔH_sub.

[TOC]

Apakah persamaan Clausisu-Clapeyron untuk?

Pengiraan tekanan tekanan dan enthalpies pengewapan

Dari persamaan Clausius-Clapeyron dari atas, beberapa pertimbangan matematik akhirnya dibuat untuk akhirnya melakukan integrasi. Sebagai contoh, untuk sistem wap cecair, diandaikan bahawa ΔH_Vap Ia tidak berbeza dengan suhu, dan ΔV sepadan dengan jumlah stim, menghina jumlah cecair (v_wap-V_cecair = V_wap).

Dengan mengandaikan bahawa stim bertindak sebagai gas yang ideal dan mengintegrasikan, persamaan clausius-clapeyron bersepadu diperolehi:

Boleh melayani anda: volatilisasi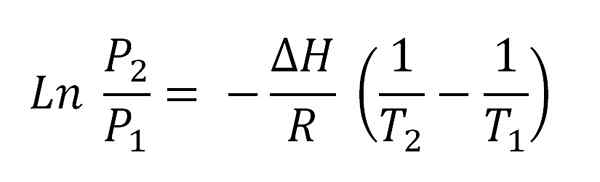 Persamaan Clausius-Clapeyron Bersepadu.

Persamaan ini sepadan dengan garis yang grafik sebagai:

Ln p vs 1/t

Dan cerun negatifnya (ΔH/r). Oleh itu, untuk memenuhi persamaan ini, ΔH mesti tetap dalam selang suhu (t₂-T₁) di mana tekanan stim diukur dalam keseimbangan dengan cecair.

Dengan cara ini, jika diandaikan bahawa ΔH bervariasi sedikit dalam selang suhu kecil, adalah mungkin untuk menggunakan persamaan garis ini untuk meramalkan perubahan dalam tekanan wap cecair; Dan lebih banyak lagi, anda boleh menentukan pengewapannya.

Semakin besar selang suhu yang dipertimbangkan, yang paling besar sisihan persamaan data eksperimen ini, dan semakin kurang ia akan dipenuhi.

Penentuan Perubahan Fasa

Oleh itu, persamaan Clausius-Clapeyron menjadi perkembangan garis tangen ke garis kewujudan bersama antara dua fasa fizikal, yang diperhatikan dalam mana-mana rajah P-T untuk bahan.

Sekiranya perubahan fasa berlaku, akan ada perubahan di cerun, dan ΔH tidak akan sama. Oleh itu, apabila penyimpangan kuat dibuktikan dan persamaan gagal, itu adalah tanda bahawa dalam selang suhu bahan mengalami perubahan fasa yang lain. Iaitu, ia tidak lagi menjadi sistem wap cecair, kerana ia diserahkan kepada garis bersama bersamaan.

Gunakan contoh

- Persamaan Clausius-Clapeyron telah digunakan dalam meteorologi untuk mengkaji tingkah laku awan, bahkan yang hadir di planet atau bulan lain dengan atmosfera.

Boleh melayani anda: asid glukonik: struktur, sifat, sintesis, kegunaan

- Ia telah digunakan dalam menentukan entalpi fusion beberapa logam seperti natrium dan gallium, dan untuk mengekstrapolasikan tekanan wap mereka pada suhu yang sangat tinggi.

- Ia juga telah digunakan untuk menentukan entalpi pengewapan bahan seperti klorin gas, karbon tetraklorida, air cair, ais dan yodium.

- Ia juga telah meneliti perubahan fasa dalam struktur kristal. Dalam contoh terakhir ini, persamaan bersepadu Clausius-Clapeyron kelihatan sangat berbeza, kerana pertimbangan yang sama yang diambil untuk sistem wap cecair tidak boleh dibuat untuk ΔV. Variasi kelantangan dari satu fasa ke yang lain kali ini kecil.

Latihan yang diselesaikan

- Latihan 1

Tekanan wap ais adalah 4.58 torr pada 0 ° C dan 1.95 torr a -10 ° C. Apakah entalpi sublimasi anda dalam julat suhu itu?

Perhatikan bahawa kami mempunyai dua tekanan dan dua suhu:

P₁ = 4.58 Torr

P₂ = 1.95 Torr

T₁ = 0 ° C + 273 = 273 k

T₂ = -10 ° C + 273 = 263 k

Kami menukar unit suhu dari ° C ke k, kerana r tetap gas mempunyai k di unitnya:

R = 8.314 J/k

Oleh itu, kami menggunakan persamaan Clausius-Clapeyron bersepadu dan jelas ΔH_sub, yang akan kekal sebagai:

ΔH_sub = -Rln (p₂/P₁) / (1 / t₂ - 1 /t₁)

Untuk keselesaan lebih lanjut akan terus menggantikan hanya dengan nombor, tetapi mengetahui bahawa unit akhir akan menjadi joule:

ΔH_sub = -(8.314) ln (1.95/4.58)/(1/263 - 1/273)

= 50.97 J

Atau 51.07 j Mempertimbangkan beberapa perpuluhan. Nilai ini akan membentangkan ayunan bergantung pada selang waktu t₂-T₁ dan tekanan stim tertentu.

- Latihan 2

Titik mendidih etanol pada tekanan 760 torr (1 atm) adalah 78.3 ° C, dan entalpi pengewapannya ialah 39.3 kJ. Apa yang akan menjadi tekanan stim anda pada suhu 46 ° C?

Ia boleh melayani anda: Tantalus: struktur, sifat, kegunaan, memperoleh

Kami mengenal pasti data:

P₁ = 760 Torr

P₂ = ?

T₁ = 78.3 ° C + 273 = 351.3 k

T₂ = 46 ° C + 273 = 319 k

ΔH_Vap = 39.3 kJ atau 39300 j

Jadi, kita mesti membersihkan p₂ persamaan Clausius-Clapeyron bersepadu. Sekali lagi, unit akan ditinggalkan untuk keselesaan dan pengiraan akan dibangunkan langkah demi langkah:

Ln (p₂/P₁) = -(ΔH_Vap/R) (1/t₂ - 1/t₁)

Ln (p₂/760) = -(39300/8.314) (1/319 - 1/351.3)

Ln (p₂/760) = -1.36

Memohon fungsi eksponen di kedua -dua belah persamaan untuk dapat membersihkan p₂ kita akan mempunyai:

E (ln p₂/760) = e^(-1.36)

P₂/760 = 0.256

P₂ = 0.256 (760)

= 195 Torr

Pada suhu yang lebih rendah (46 ° C), tekanan stim yang lebih rendah (195 Torr). Malah, mempunyai etanol tekanan 760 torr hingga 78.3 ° C, kita bercakap mengenai titik mendidih biasa. Ini adalah tingkah laku yang diharapkan untuk semua cecair

Secara umum, latihan Clausius-Clapeyron jenis ini terdiri daripada penjelasan p₂, T₂ atau ΔH pengewapan atau sublimasi. Pengiraan berubah dengan ketara apabila ΔV juga harus dipertimbangkan, terutamanya apabila ia berkaitan dengan sistem atau baki pepejal cecair.

Rujukan

1. Whitten, Davis, Peck & Stanley. (2008). Kimia. (8th ed.). Pembelajaran Cengage.
2. Wikipedia. (2020). Hubungan Clausius-Clapeyron. Diperoleh dari: dalam.Wikipedia.org
3. Universiti Negeri San José. (s.F.). Persamaan Clausius-Clapeyron:
   Derivasi dan aplikasi STI dalam Meteorologi. Pulih dari: SJSU.Edu
4. Kumpulan Bodner. (s.F.). Persamaan Clausius-Clapeyron. Diperolehi daripada: Chemed.Chem.Purdue.Edu
5. Chieh c. & Censulo a. (18 Mei 2020). Persamaan Clausius-Clapeyron. Kimia Librettexts. Pulih dari: chem.Libretxts.org
6. Walter J. Moore. (1962). Kimia Fizikal. (Edisi Keempat). Longmans.