Persamaan pecahan
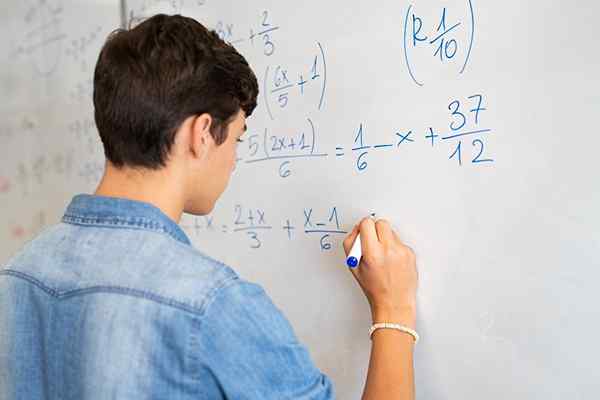
- 4276
- 1080
- Kerry Schmitt
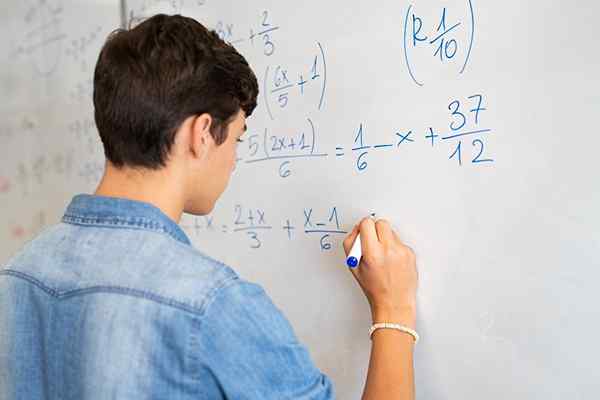 Persamaan pecahan termasuk pecahan berangka dan/atau algebra, dan yang tidak diketahui mungkin dalam pengangka dan penyebut, atau kedua -duanya
Persamaan pecahan termasuk pecahan berangka dan/atau algebra, dan yang tidak diketahui mungkin dalam pengangka dan penyebut, atau kedua -duanya Apakah persamaan pecahan?
The Persamaan pecahan adalah yang mengandungi pecahan dalam satu atau lebih istilah mereka. Pecahan sedemikian boleh berangka atau algebra, di mana yang tidak diketahui boleh didapati dalam pengangka dan/atau dalam penyebut apa -apa istilah.
Kemudian, beberapa contoh persamaan pecahan dengan satu yang tidak diketahui:
Contoh pertama adalah persamaan linear dengan pekali pecahan; Dalam contoh kedua, yang tidak diketahui adalah dalam penyebut setiap istilah, dan pada yang terakhir, yang tidak diketahui adalah pengangka dan penyebutnya.
Untuk menyelesaikannya, adalah perlu untuk menjalankan beberapa transformasi algebra dan dengan itu mendapatkan persamaan yang setara, di mana yang tidak diketahui tidak muncul dalam penyebut. Sebaik sahaja prosedur ini dilakukan, penyelesaiannya dijumpai menggunakan teknik yang sesuai.
Penyelesaiannya terdiri daripada set nilai "x" yang memenuhi persamaan. Ia boleh menjadi nilai yang unik, atau beberapa, tetapi, dalam apa jua keadaan, sangat penting untuk diingat bahawa tidak semua penyelesaian dalam persamaan bersamaan boleh diterima oleh persamaan asal.
Sesungguhnya, jika ia adalah persamaan yang tidak diketahui adalah dalam penyebut, nilai "x" yang membatalkannya harus dielakkan, walaupun mereka tergolong dalam set penyelesaian persamaan bersamaan. Ini kerana pembahagian antara 0 tidak ditakrifkan.
Sekiranya persamaan bersamaan mempunyai penyelesaian yang unik, dan ternyata penyebut mana -mana terma persamaan asal dibatalkan, maka ia tidak mempunyai penyelesaian.
Cara menyelesaikan persamaan pecahan
Operasi yang dijalankan untuk menyelesaikan persamaan bukan -fractional adalah sah, dengan syarat kesamaan dikekalkan. Dengan cara ini, dalam persamaan pecahan anda boleh menambah atau menolak kuantiti yang sama ke kedua -dua belah persamaan, kalikan semua istilah dengan jumlah yang sama, atau membahagikan setiap istilah dengan jumlah yang sama (berbeza dari 0).
Boleh melayani anda: Teorem BolzanoTetapi kerana persamaan pecahan diperlukan untuk berubah menjadi setara yang lain tanpa penyebut, petunjuk umum berikut juga diikuti:
- Cari pelbagai penyebut minimum (m.c.m).
- Melipatgandakan setiap istilah dengan m.c.m., Untuk menghapuskan penyebut.
- Selesaikan persamaan bersamaan yang diperoleh.
- Sahkan bahawa penyelesaian yang dijumpai memenuhi persamaan asal.
Jenis persamaan yang setara
Persamaan bersamaan yang diperoleh berikutan prosedur yang ditunjukkan boleh:
- Ijazah linear atau pertama
- Kuadratik
- Perintah yang lebih tinggi
Contoh yang diselesaikan
Contoh 1
Selesaikan persamaan berikut:
Diperhatikan bahawa persamaan adalah ijazah pertama dalam "x", sebagai "x" tinggi pada 1. Koefisien persamaan adalah pecahan dan cara untuk menghapuskannya, untuk bekerja dengan nombor keseluruhan, ia mengalikan semua terma dengan pelbagai penyebut minimum (m.c.m.).
m.c.m. (2,3,6) = 6
Jadi:
3x - 2x = 1
x = 1
Pembaca boleh menyemak kesahihan penyelesaian ini, menggantikan x = 1 dalam persamaan asal dan mengesahkan bahawa kesamaan diperolehi.
Contoh 2
Tentukan nilai "x" yang memenuhi:
Tidak seperti contoh terdahulu, dalam kes ini, yang tidak diketahui didapati dalam penyebut. Perhatikan bahawa penyebutnya dibatalkan untuk nilai x = 2 dan x = -1, perincian yang mudah diambil kira, kerana, jika persamaan bersamaan mengakui penyelesaian ini, kita mesti membuangnya, kerana mereka tidak dapat diterima dalam persamaan asal.
Sekarang kita mesti mengubah persamaan ke dalam yang lain tanpa penyebut, langkah pertama adalah untuk membuat jumlah istilah di sebelah kiri persamaan:
Oleh kerana penyebutnya adalah sama, sehingga kesamaan dipenuhi, adalah perlu bahawa pengangka juga menjadi:
Boleh melayani anda: pemalar berkadar: apakah, pengiraan, latihan4 (x+1) - 3 (x -2) = 8
Sudah cukup untuk menyelesaikan persamaan ini, yang ternyata menjadi gred pertama:
4x + 4 - 3x + 6 = 8
x = 8 - 6 - 4 = - 2
x = - 2
Oleh kerana nilai ini berbeza daripada nilai yang dilarang, ia diterima sebagai penyelesaian persamaan asal.
Contoh 3
Cari penyelesaian:
Dalam persamaan ini, nilai x = 4 membatalkan penyebut, oleh itu, ia dikecualikan daripada set penyelesaian persamaan yang diubah, jika muncul.
Persamaan yang diubah mudah dicari, sudah cukup untuk membiak semua istilah dengan faktor (x-4):
Menginap:
2x - 4 = 4
2x = 8
x = 4
Contoh 4
Selesaikan persamaan:
Dalam kes ini, penyebut mempunyai istilah kuadrat, jadi mudah untuk memaparkannya terlebih dahulu:
- x2 + 8x + 7 = (x + 7) (x + 1)
- x2 - 49 = (x + 7) (x - 7)
- x2 - 6x - 7 = (x - 7) (x + 1)
Persamaannya seperti ini:
Nilai x yang membatalkan mana -mana penyebut adalah: x = -7, x = 7, x = -1. Oleh itu, walaupun nilai -nilai ini adalah sebahagian daripada penyelesaian set persamaan yang diubah suai, mereka tidak boleh menjadi penyelesaian persamaan asal.
Kini datang proses mengubah persamaan. Langkah pertama ialah mencari pelbagai penyebut minimum:
m.c.m. = (x + 7) (x - 7) (x + 1)
Dengan mengalikan kedua -dua belah persamaan dengan m.c.m. ditinggalkan:
Hasil:
(x --7) (x- 2) = (x + 1) (2x - 5) - (x + 7) (x - 2)
Melalui harta pengedaran produk dibangunkan:
x2 - 9x +14 = 2x2 - 3x - 5 - (x2 + 5x - 14)
Mengurangkan istilah yang serupa di sebelah kanan:
x2 - 9x + 14 = x2 - 8x + 9
Istilah kuadrat dibatalkan, dengan memenuhi tanda yang sama di sisi persamaan yang berbeza:
Boleh melayani anda: Perbezaan kiub: formula, persamaan, contoh, latihan- 9x + 14 = - 8x + 9
-x = -5 ⇒ x = 5
Hasil ini dimasukkan sebagai penyelesaian, kerana ia bukan mana -mana nilai yang dilarang.
Latihan permohonan persamaan pecahan
Penyebut pecahan melebihi empat unit kepada pengangka. Jika pengangka dikurangkan dari pengangka dan penyebut juga, pecahan yang dihasilkan adalah 3/5. Tentukan pecahan asal.
Penyelesaian
Biarkan x menjadi nilai pengangka.
Oleh kerana penyebut pecahan melebihi empat unit kepada pengangka, pecahan asal adalah:
Sekarang anda perlu tolak 5 unit, baik kepada pengangka dan penyebut:
Oleh kerana pecahan yang terhasil daripada menjalankan prosedur sebelumnya adalah sama dengan 3/5, mereka disamakan:
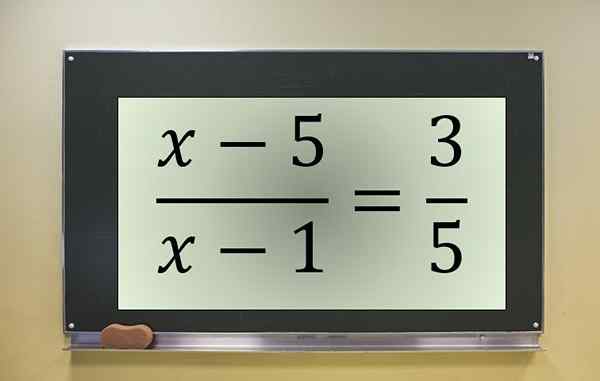 Contoh persamaan pecahan. Sumber: f. Zapata.
Contoh persamaan pecahan. Sumber: f. Zapata. Ini adalah persamaan pecahan dengan yang tidak diketahui dalam pengangka dan penyebut, yang dibatalkan pada x = 1. Oleh itu, nilai ini mesti dikecualikan, jika ia adalah antara penyelesaian persamaan yang diubah.
Kemudian, ia melipatgandakan kedua -dua belah pihak dengan pelbagai minimum, iaitu 5 (x - 1):
Mengakibatkan persamaan bersamaan berikut:
5 (x - 5) = 3 (x - 1)
Memohon harta pengedaran:
5x -25 = 3x - 3 ⇒ 2x = 22
x = 11
Pecahan asal menggantikan x = 11 dalam ungkapan:
Hasil pecahan 11/15. Inilah jawapan kepada masalah yang dibangkitkan.
Rujukan
- Persamaan pecahan. Pulih dari: Mathepower.com
- Portal Matematik. Persamaan pecahan. Resolusi masalah. Pulih dari: silvioduarte.com.
- Stewart, J. (2007). Preccculment: Matematik untuk Pengiraan. 5th. Edisi. Pembelajaran Cengage.
- Sullivan, m. (1997). Precalculation. Ke -4. Edisi. Pendidikan Pearson.
- Zill, d. (2008). Preccculment dengan kemajuan pengiraan. Ke -4. Edisi. McGraw Hill.



(x+1))

=6\left%20(%20\frac16%20\right%20))
-3(x-2)(x-2)(x+1)=\frac8(x-2)(x+1))
\left%20(%20\fracxx-4%20\right%20)+(x-4)=(x-4)\left%20(%20\frac4x-4%20\right%20))

(x+1)=\frac2x-5(x+7)(x-7)-\fracx-2(x-7)(x+1))
(x-7)(x+1)\left%20[%20\fracx-2(x+7)(x+1)%20\right%20]=(x+7)(x-7)(x+1)\left%20[%20\frac2x-5(x+7)(x-7)-\fracx-2(x-7)(x+1)%20\right%20])



\left%20(%20\fracx-5x-1%20\right%20)=5(x-1)\frac35)