Hendecagon

Apa itu endecagon?

Dia Hendecagon, juga dipanggil Undecágono, Ia adalah tokoh geometri rata dengan 11 sisi yang dimiliki oleh keluarga poligon.

Ini dilantik mengikut jumlah pihak yang mereka ada dan dalam hal endecagon, nama mereka berasal dari kata -kata Yunani "Hendeka" dan "Gona": sebelas dan puncak, masing -masing, menurut fakta bahawa endecagon itu mempunyai 11 simpul atau petua.

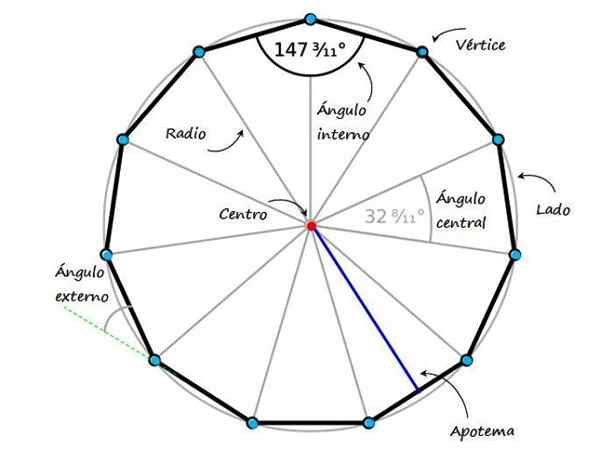
Rajah 1. Endecagon biasa dan elemennya. Sumber: f. Kasut wikimedia yang diubahsuai.

Poligon biasa berkongsi satu siri ciri tersendiri, khususnya. Rajah 1 menunjukkan endecagon biasa dan sifat yang paling penting:

• Sisi, Sejumlah 11.
• Simpang, Terdapat juga 11 mata yang menyertai dua sisi berturut -turut (dalam angka sebelumnya adalah titik biru dan dalam Rajah 3 mereka juga dinamakan dengan huruf besar).
• Pusat, Titik yang sama dari kedua -dua simpang dan sisi.
• Diagonal, Garis yang menyertai puncak dengan puncak yang tidak berturut -turut, sebanyak 44.
• Sudut dalaman, Mereka yang terbentuk di antara dua sisi bersebelahan di bahagian dalaman endecagon. Sekiranya endecagon biasa, semua sudut dalaman mengukur 147 ^3/11 º.
• Sudut luaran, Mereka dibentuk di antara satu sisi dan pemanjangan salah satu sisi berturut -turut.
• Radio, Jarak dari pusat ke puncak.
• Sudut pusat, bahawa dalam kes endecagon biasa berukuran 32 ^11/11 º, sisinya adalah dua segmen bersebelahan dan puncak sudut bertepatan dengan pusat.
• Apothem, segmen tegak lurus yang menyertai pusat satu sisi dengan pusat angka.

Ia boleh melayani anda: Hipparco of Nicea: Biografi dan Sumbangan kepada Sains

Cara membuat endecagon biasa?

Untuk melukis endecagon biasa, yang sisinya mengukur sama, anda memerlukan peraturan dan kompas. Salah satu cara untuk membuat susun atur mengikuti langkah -langkah ini:

1.- Lukiskan lilitan dan dua diameternya, satu menegak dan satu lagi mendatar. Titik lilitan yang ditentukan oleh diameter ini dinamakan dan B (diameter mendatar) dan C dan D (diameter menegak).

2.- Buka kompas dengan ukuran jejari bulatan, menyokong hujung pada titik d diameter Cd dan lukis arka pertama yang memotong lilitan pada titik e.

3.- Dengan langkah yang sama ini menyokong hujung kompas pada titik A dan lukis gerbang kedua yang merentasi lilitan pada titik f dan pada masa yang sama melewati pusat yang sama.

4.- Buka pukulan dengan hujung yang disokong oleh E dan ke titik F, lukis arka ketiga yang memotong diameter menegak pada titik g.

5.- Sekarang, buka kompas antara mata f dan g. Ini akan menjadi ukuran bahagian endecagon. Hujung kompas disokong dalam f dan menarik arka keempat yang memotong ke lilitan pada titik H, sisi FH sudah milik endecagon dan ditarik dengan menyertai mata dengan bantuan peraturan.

6.- Hujung kompasnya berturut -turut pada titik H dan disediakan dengan teliti, menyertai titik -titik yang ditentukan oleh segmen, sehingga sebelas sisi poligon.

Contoh Endecágonos

Terdapat beberapa jenis endecargon, mengikut ukuran sisi mereka dan sudut dalaman mereka, di bawah beberapa contoh:

Endeconis biasa dan tidak teratur

-Biasa, Sekiranya semua sisi dan sudut dalaman mengukur sama.

Boleh melayani anda: Nombor Euler atau Nombor E: Berapa OK, Properties, Aplikasi

-Tidak teratur, Apabila pihak mereka mempunyai ukuran yang berbeza.

Angka berikut menunjukkan endecagon biasa dalam kontur dalaman dolar AS dengan angka Susan B. Anthony (1820-1906), seorang aktivis hak wanita yang dilahirkan di Massachusetts, Amerika Syarikat. Endecagon juga telah digunakan sebagai sebahagian daripada reka bentuk duit syiling lain di seluruh dunia.

Rajah 2. Endecagon biasa yang membentuk sebahagian daripada reka bentuk Dolar Susan B. Anthony, dicipta antara tahun 1979 dan 1981, dan kemudian dilancarkan semula pada tahun 1999. Sumber: Wikimedia Commons.

Endecargon cembung dan cekung

Endecargon berbeza mengikut sudut dalaman mereka, contohnya mereka boleh:

-Cembung, Sekiranya sudut dalaman kurang daripada 180º.

-Cekung, Apabila terdapat sudut dalaman lebih besar daripada 180º.

Endecagon yang menghiasi dolar susan b. Anthony adalah cembung, kerana ukuran mana -mana sudut dalamannya kurang dari 180º. Nilainya dikira melalui formula yang bergantung kepada bilangan sisi pada angka (lihat bahagian berikut).

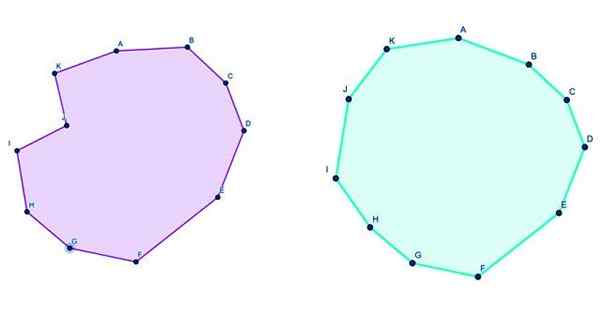Rajah 3. Ke kiri endecagon cembung dan ke kanan endecagon cekung. Sumber: f. Zapata melalui geogebra.

Formula untuk endecagon

Formula untuk sudut dalaman

Untuk menentukan ukuran I dalam darjah, sudut dalaman poligon biasa n sisi, formula berikut digunakan:

 Menggantikan bilangan sisi endecagon n = 11 dalam formula diperolehi:

 Dan kerana sudut dalaman endecagon biasa kurang dari 180º, angka ini adalah poligon cembung.

Jumlah sudut dalaman poligon biasa ditemui oleh formula ini, sah untuk keseluruhan dan lebih besar daripada 2:

Boleh melayani anda: sudut dalam lilitan: jenis, sifat, latihan yang diselesaikan

S = (n - 2) x 180º

Menggantikan N = 11 Hasil:

S = (11 - 2) x 180º = 1620º

Sudut luaran

Untuk mengetahui ukuran sudut dalaman, ia digunakan bahawa jumlah sudut dalaman dan luaran adalah sama dengan 180º:

180 º - 147 ^3/11º = 32 ^11/11º.

Perimeter

Perimeter adalah jumlah sisi endecagon, sama ada biasa atau tidak. Dalam kes endecagon biasa, jika ℓ Ia adalah panjang satu sisi, perimeter berlipat ganda n, Jumlah sisi.

Oleh itu perimeter p dari endecagon biasa adalah:

P = 11 ℓ

Kawasan

Mengetahui sisi, kawasan ini boleh dikira dengan formula:

Yang kira -kira:

A = 9.3656 ∙ ℓ²

Satu lagi cara untuk mencari kawasan itu, dengan syarat bahawa endecagon adalah biasa, adalah untuk membahagikannya ke segitiga asas yang sama dengan sisi ℓ dan ketinggian sama dengan panjang apothem l l_Ke.

Kawasan setiap segitiga dikira oleh:

Kawasan = asas x ketinggian /2

Itu bergantung kepada apothem juga ditulis sebagai:

Kawasan = ℓ. L_Ke /2

Dan jumlah kawasan endecagon mengalikan kawasan segitiga dengan 11:

A = 11ℓ. L_Ke /2

Dari segi perimeter, kawasan endecagon biasa adalah:

A = p. L_Ke /2

Diagonal

Bilangan pepenjuru dikira dengan melakukan n = 11 dalam formula berikut:

 D = [11 x (11-3)]/2 = 44 Diagonal.

Latihan diselesaikan

Kirakan perimeter dan kawasan endecagon biasa sebanyak 20 cm.

Penyelesaian

Perimeter adalah:

P = 11 ℓ =11 × 20 cm = 220 cm.

Dan kawasannya adalah:

A = 9.3656 ∙ ℓ²= 9.3656 × (20 cm)²= 3746.2 cm²

Rujukan

1. Alexander, d. 2013. Geometri. 5th. Edisi. Pembelajaran Cengage.
2. Profesor Lukisan. Endecágono ditulis dalam lilitan (11 sisi poligon). Pulih dari: youtube.com.
3. Masalah dan persamaan. Kalkulator kawasan dan perimeter endecagon biasa. Diperoleh dari: masalah syuses.com.
4. Matematik Sangaku. Unsur poligon dan klasifikasinya. Pulih dari: Sangakoo.com.
5. Menyelesaikan masalah geometri automatik. Endecagon. Pulih dari: scuolaetrica.Item.
6. Wolfram Mathworld. Hendecagon. Pulih dari: Mathworld.Wolfram.com.