Matematik

Nilai mutlak

Nilai mutlak

Apakah nilai mutlak?

Dia nilai mutlak nombor sebenar ditakrifkan sebagai jarak antara nombor itu dan 0 garis sebenar. Untuk jarak, nilainya sentiasa positif atau sifar dan sama dengan angka nombor.

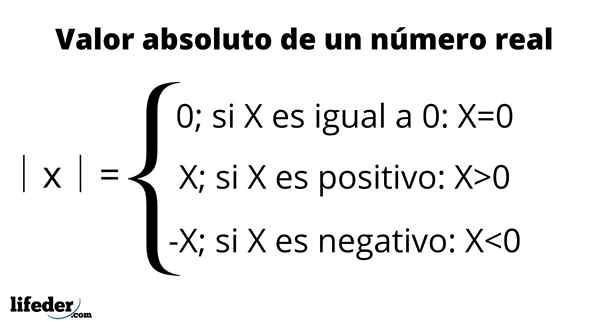
Nilai mutlak diwakili dengan meletakkan nombor antara dua bar menegak, simbol yang dibaca: "nilai mutlak", Seperti yang diringkaskan dalam jadual berikut:

Sebagai contoh, nilai mutlak -3 ditulis sebagai │ -3│ dan sama dengan 3. Ini bermakna bahawa antara -3 dan 0 terdapat tiga unit, yang mewakili nombor pada garis sebenar. Sebaliknya, nilai mutlak +3 atau hanya 3, juga sama dengan 3, kerana dengan mengukur jaraknya ke 0 ia juga tiga unit.

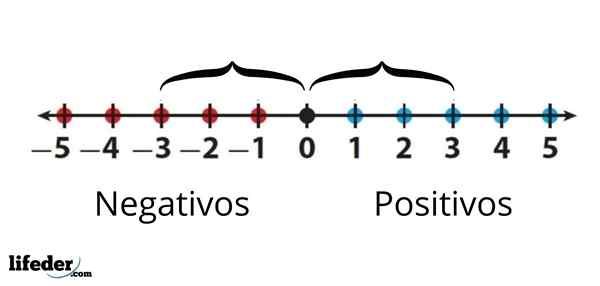Nilai mutlak -3 adalah sama dengan nilai mutlak +3, kerana jarak antara sama ada hingga 0 adalah sama adalah sama

Ringkasnya, nilai mutlak nombor adalah angka yang sama nombor tetapi selalu dengan tanda positif.

Sifat nilai mutlak

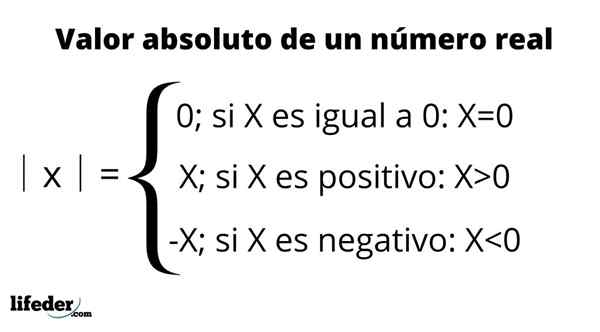Definisi nilai mutlak

Sifat utama nilai mutlak:

  • 1) Nilai mutlak nombor sentiasa positif atau 0, oleh itu:

│x│≥ 0

  • 2) Nilai mutlak sifar juga sifar, iaitu │0 │ = 0, oleh itu ia boleh disahkan bahawa:

│x│ = 0, ya y hanya jika x = 0

  • 3) Bagi setiap nombor x yang dimiliki oleh set nombor sebenar, nilai mutlak x adalah sama dengan nilai mutlak - x:

│x│ = │ - x│

  • 4) Jika nilai mutlak nombor x adalah, ini bermakna terdapat dua pilihan untuk nombor itu: i) x = +a atau ii) x = -a.
Ia boleh melayani anda: Mary mengembara 2/4 dari CyclePist, Melissa Travels 4/8 dan Anahi Perjalanan 3/6

Contohnya, jika nilai mutlak nombor adalah 5, kedua -dua kemungkinan adalah nombor itu +5 atau -5.

Operasi dengan nilai mutlak

Ciri -ciri berikut sangat berguna untuk melakukan operasi dengan nilai mutlak:

  • 5) Untuk "x" dan "y" yang merupakan dua nombor sebenar, ketidaksamaan berikut selalu dipenuhi, dipanggil ketidaksamaan segi tiga nilai mutlak:

│x│+│y│≥ │x+y│

Sebagai contoh, jadilah:

x = -6

y = 9

Bahagian kiri ketidaksamaan adalah:

│-6│ + │9│ = 6 + 9 = 16

Dan sebelah kanan adalah:

│-6+9│ = │3│ = 3

Jelas 16 lebih besar daripada atau sama dengan 3, dan ini selalu berlaku apabila nombor x dan dan mempunyai tanda yang berbeza. Sekiranya mereka mempunyai tanda yang sama, maka kesamaan diperolehi. Lihat contoh lain dengan dua nilai lain yang berbeza:

x = -5

y = -3

│-5│+│-3│≥ │-5-3│

5+3≥ │-8│

Malah:

8 = 8

  • 6) Produk nilai mutlak masing -masing dua nombor sebenar "x" dan "y" adalah sama dengan nilai mutlak produk nombor:

│x│ ∙ │y│ = │x ∙ y│

Sekali lagi adalah nilai -nilai:

x = -6

y = 9

Jadi:

│-6│ ∙ │9 │ = 6 ∙ 9 = 54

Yang sama dengan:

│ (-6) ∙ 9 │ = │-54│ = 54

  • 7) Kota nilai mutlak dua nombor nyata "x" dan "y", dengan penyebut yang berbeza 0, adalah nilai mutlak dari quotient antara nombor -nombor ini:

Selagi dan ≠ 0.

Contoh:

Contoh nilai mutlak

Contoh mudah

Mengira nilai mutlak mana -mana nombor sebenar adalah sangat mudah, contohnya nilai mutlak nombor berikut adalah:

a) │ 14 │ = 14

b) │-(-5) │ = │5│ = 5

c) │π│ = π

Pengiraan dengan nilai mutlak nombor sebenar

Lakukan operasi berikut yang melibatkan nilai mutlak:

a) 2 ⋅ │8│ + 5 ⋅ -16│ -⋅ │4│ = (2 ⋅8) + (5 ⋅16) - 4 = 16 + 80 - 4 = 92

b) │5- (8 ⋅3) │- 6 + │81 ÷ (-3) │ 

Boleh melayani anda: separuh daripada 15

Ini adalah operasi gabungan, jadi lebih baik menyelesaikannya dengan langkah -langkah. Nilai mutlak pertama ialah:

│5- (8 ⋅3) │ = │5-24│ = │-19│ = 19

Nilai mutlak kedua yang muncul dikira seperti berikut:

│81 ÷ (-3) │ = │-27│ = 27

Kemudian hasil yang diperoleh dikumpulkan dan pengiraan akhir dijalankan:

│5- (8 ⋅3) │- 6 + │81 ÷ (-3) │ = 19- 6 + 27 = 40

Jarak antara dua mata di garisan sebenar

Nilai mutlak muncul dalam banyak aplikasi, seperti mencari jarak antara dua nombor yang tergolong dalam garis sebenar. Jika A adalah nombor sebenar maka ia terletak di garisan sebenar pada titik yang abscissa adalah "a", yang sama berlaku dengan nombor sebenar b.

Biarkan "A" dan "B" dua nombor pada garis sebenar, jarak yang memisahkannya adalah:

dAb = │b - a│

Yang juga boleh dikira oleh:

dAb = │a - b│

Sebagai contoh, jarak antara a = 5 dan b = 12 adalah:

D = │5-12│ = │12-5│ = 7

Dengan cara ini, nilai mutlak penolakan antara dua nombor nyata hanyalah jarak yang memisahkannya pada baris sebenar.

Fungsi nilai mutlak

Fungsi nilai mutlak adalah aplikasi yang berjalan pada set nombor nyata ℛ sehingga ℛ+, yang sepadan dengan setiap nombor sebenar nilai mutlaknya. Ia ditakrifkan oleh:

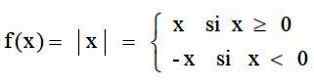
Dan grafnya mempunyai bentuk V biasa:

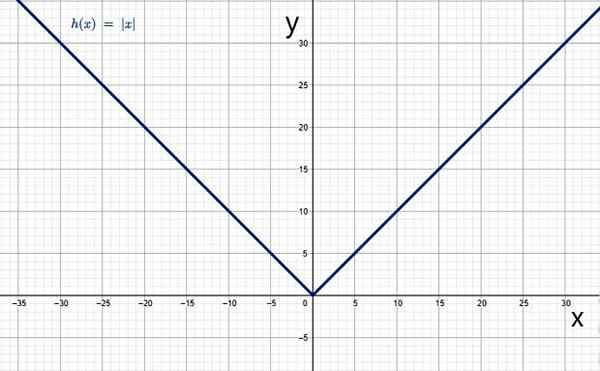Nilai mutlak sebagai fungsi. Sumber: f. Zapata melalui geogebra.

Ciri -ciri fungsi nilai mutlak

-Domain anda adalah set semua nombor sebenar.

-Ia berterusan.

-Walaupun begitu, kerana ia dipenuhi bahawa f (x) = f (-x), oleh itu paksi menegak adalah paksi simetri.

-Julat fungsi nilai mutlak adalah set sebenar yang positif termasuk 0, kerana fungsi selalu mewakili jarak, dan ini selalu positif atau batal.

Boleh melayani anda: apakah panduannya? (Geometri)

-Ia adalah fungsi mengikut bahagian atau oleh bahagian.

-Berkurangan dalam selang (-∞, 0) dan tumbuh dalam (0,+∞).

Hujah nilai mutlak juga boleh menjadi kuadrat atau fungsi lain, sebagai contoh, ia boleh ditakrifkan:

  • f (x) = │x2-5x+3│
  • g (x) = │sen x│

Nilai mutlak bertanggungjawab untuk menjadi positif imej hujah yang mempunyai tanda negatif.

Latihan yang diselesaikan

Latihan 1

Menilai ungkapan algebra berikut dengan nilai mutlak:

a) │2x -5 │ + │ --x + 1 │ pada x = 3

b) │ (x - 5) ÷ (x+4) │ pada x = -1

Penyelesaian kepada

│2 ⋅3-5 │ + │ - 3 + 1 │ = │6-5│ + │ - 2│ = │1│ + 2 = 3

Penyelesaian b

│ (-1-5) ÷ (-1+4) │ = │ (-6) ÷ (3) │ = │ - 2 │ = 2

Latihan 2

Apakah set nilai yang mewakili ketidaksamaan berikut?

│x│≤ 3

Penyelesaian

Ketidaksamaan mewakili semua nombor sebenar yang nilai mutlaknya kurang daripada atau sama dengan 3, oleh itu ia adalah set semua nombor antara -3 dan +3, termasuk ini.

Dalam notasi selang ia tetap:

[-3,3]

Latihan 3

Selesaikan persamaan berikut dengan nilai mutlak:

│2x-1│ = 5

Penyelesaian 

Seperti yang dinyatakan sebelum ini, untuk menyelesaikan persamaan dengan nilai mutlak, perlu mempertimbangkan kedua -dua pilihan. Maksud saya, ya:

│f (x) │ = c

Jadi:

1) f (x) = c

2) f (x) = -c

Oleh itu persamaan ini, yang hujahnya linear, mempunyai dua penyelesaian:

Penyelesaian pertama

2x - 1 = 5

2x = 6 ⇒ x1 = 3

Penyelesaian kedua

2x - 1 = -5

2x = -4 ⇒ x2 = -2

Apabila menilai x1 = 3 atau x2 = -2 Dalam persamaan asal kesamaan mesti diperolehi, dengan cara ini disahkan bahawa nilai yang diperolehi adalah penyelesaian persamaan yang dicadangkan. Malah:

│ (2 ⋅3) -1 │ = │6-1│ = 5

Dan apabila mencuba dengan pilihan kedua, kesamaan juga diperolehi:

│2 ⋅ (-2) -1│ = │-4-1│ = 5

Rujukan

  1. Baldor, a. 2005. Algebra. Kumpulan tanah air budaya.
  2. Larson, r. 2012. Precalculation. Ke -8. Edisi. Pembelajaran Cengage.
  3. Hoffman, J. Pemilihan masalah matematik. Jilid 2.
  4. Stewart, J. 2007. Preccculment: Matematik untuk Pengiraan. 5th. Edisi. Pembelajaran Cengage.
  5. Zill, d. 1984. Algebra dan trigonometri. McGraw Hill.