Sifat enegon, cara membuat enegon, contoh

A Enegon Ia adalah poligon sembilan sisi dan sembilan simpul, yang boleh biasa atau tidak. Denominasi enegon berasal dari bahasa Yunani dan terdiri daripada kata -kata Yunani Ennea (sembilan dan Gonon (Sudut).

Nama alternatif untuk poligon sembilan yang tidak disengajakan adalah perkataan bukan kata yang berasal dari bahasa Latin nonus (sembilan dan Gonon (puncak). Sebaliknya, jika sisi atau sudut enegon tidak sama rata antara satu sama lain, maka ada a Enegon yang tidak teratur. Jika sebaliknya, sembilan sisi dan sembilan sudut enegon adalah sama, maka itu adalah enegon biasa.

Rajah 1. Enegon biasa dan enegon yang tidak teratur. (Huraian sendiri)

[TOC]

Sifat enegon

Untuk poligon n sisi jumlah sudut dalamannya ialah:

(N - 2) * 180º

Dalam enegon ia akan menjadi n = 9, jadi jumlah sudut dalamannya adalah:

SA = (9 - 2) * 180º = 7 * 180º = 1260º

Di mana -mana poligon, bilangan pepenjuru adalah:

D = n (n - 3) / 2 dan dalam kes enegon, sebagai n = 9, anda perlu d = 27.

Enegon biasa

Di enegon atau nonagon biasa.

Ia kemudiannya perlu untuk mengukur sudut dalaman enegon ialah 1260º / 9 = 140º.

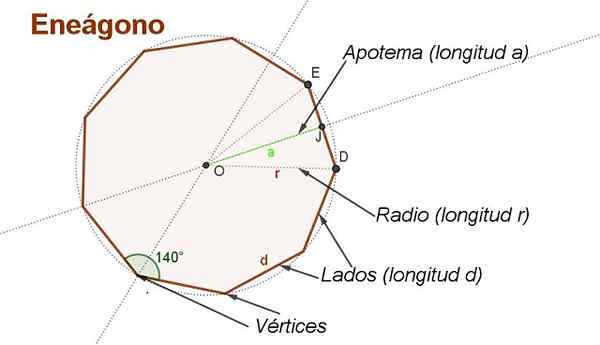Rajah 2. Apothem, radio, sisi, sudut dan simpul enegon biasa. (Huraian sendiri)

Untuk menyimpulkan formula kawasan enegon biasa di sebelah d Adalah mudah untuk membuat beberapa pembinaan tambahan, seperti yang ditunjukkan dalam Rajah 2.

Pusat ini Sama ada Melukis MediTrices dari dua sisi bersebelahan. Pusat Sama ada Equidista dari simpang.

Jejari panjang r Ia adalah segmen yang pergi dari pusat Sama ada Di puncak enegon. Radio ditunjukkan dalam Rajah 2 OD dan OE panjang r.

Boleh melayani anda: simetri

Apothem adalah segmen yang pergi dari pusat ke titik tengah di satu sisi enegon. Sebagai contoh OJ Ia adalah apothem yang panjangnya ke.

Kawasan enegon yang diketahui dan apothem

Kami menganggap segitiga Ode Dari Rajah 2. Kawasan segitiga ini adalah produk pangkalannya Dari dengan ketinggian OJ dibahagikan dengan 2:

Kawasan Ode = (Dari * oj) / 2 = (D * A) / 2

Oleh kerana terdapat 9 segitiga kawasan yang sama di Enegon, disimpulkan maka kawasan yang sama adalah:

Kawasan Enegon = (9/2) (d * a)

Kawasan enegon yang diketahui

Sekiranya hanya panjang enegon yang diketahui, maka perlu mencari panjang apothem untuk dapat memohon formula bahagian sebelumnya.

Kami menganggap segitiga Oje Segi empat tepat di J (Lihat Rajah 2). Jika nisbah trigonometri tork digunakan, ia diperolehi:

Jadi (∡Oej) = OJ / Cth.

Sudut ∡oej = 140º / 2 = 70º, kerana menjadi Eo Bisektor sudut dalaman enegon.

Selain, OJ Ia adalah apothem panjang ke.

Kemudian sebagai J Ia adalah titik tengah Ed Ia mengikutinya Ex = D/2.

Menggantikan nilai di atas dalam hubungan tangen adalah:

Tan (70º) = A / (D / 2).

Sekarang kita membersihkan panjang apothem:

A = (d/2) Tan (70º).

Hasil sebelumnya digantikan dalam formula kawasan untuk mendapatkan:

Kawasan Enegon = (9/2) (d * a) = (9/2)( D * (d/2) Tan (70º))

Akhirnya terdapat formula yang membolehkan kawasan enegon biasa diperoleh jika hanya panjang yang diketahui d dari sisinya:

Kawasan Enegon = (9/4) d² Tan (70º) = 6,1818 d²

Perimeter enegon biasa mengetahui sisinya

Perimeter poligon adalah jumlah sisinya. Dalam kes enegon, seperti setiap sisi, ia mengukur panjangnya d, Perimeternya akan menjadi jumlah sembilan kali d, iaitu:

Boleh melayani anda: persamaan polinomial

Perimeter = 9 d

Perimeter enegon mengetahui radionya

Memandangkan segitiga Oje Segi empat tepat di J (Lihat Rajah 2), sebab trigonometri Cosen digunakan:

cos (∡Oej) = Cth / OE = (d / 2) / r

Di mana anda diperoleh:

D = 2r cos (70º)

Menggantikan hasil ini, formula perimeter diperolehi sebagai fungsi radius enegon:

Perimeter = 9 d = 18 r cos (70º) = 6,1564 r

Cara membuat enegon biasa

1- Untuk membina enegon biasa, dengan peraturan dan kompas, ia berdasarkan lilitan c yang dibentangkan ke enegon. (Lihat Rajah 3)

2- Dua garis tegak lurus ditarik melalui pusat atau lilitan. Kemudian persimpangan a dan b salah satu baris ditandakan dengan lilitan.

3- Dengan Kompas, Membuat Pusat di Pemintasan B dan Pembukaan Sama dengan Radius Bo.

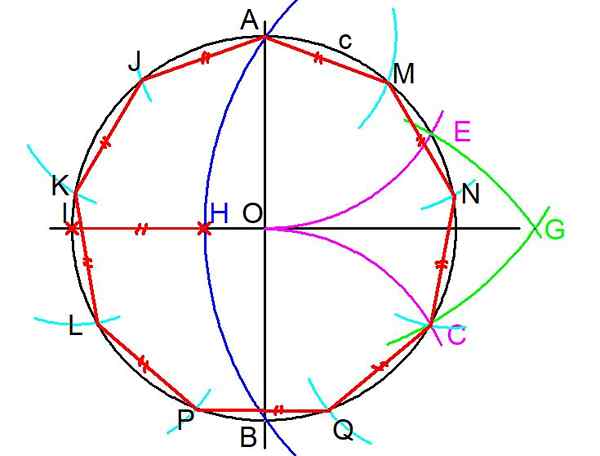Rajah 3. Langkah untuk membina enegon biasa. (Huraian sendiri)

4- Langkah sebelumnya diulang tetapi membuat pusat di A dan Radio AO gerbang ditarik yang memintas ke lilitan c pada titik e.

5- dengan pembukaan dan pusat AC dalam arka lilitan ditarik. Begitu juga dengan pembukaan dan pusat b gerbang lain ditarik. Persimpangan kedua -dua gerbang ini ditandakan sebagai g.

6- Membuat pusat di G dan dengan GA Membuka arka ditarik yang memintas paksi sekunder (mendatar dalam kes ini) pada titik h. Persimpangan paksi sekunder ditandakan dengan lilitan asal c sebagai i.

7- Panjang segmen IH adalah sama dengan panjang d di sisi enegon.

8- Dengan Pembukaan Kompas IH = D Gerbang Pusat berturut-turut ditarik ke Radio AJ, Centro J Radio AK, KL Radio KL dan Centro L Radio LP.

Ia boleh melayani anda: transformasi linear: sifat, apakah penggunaan, jenis, contoh

9- Begitu juga, bermula dari A dan di sebelah kanan, Radio Arcos ih = D ditarik pada lilitan asal C Point M, N, C dan Q.

10- Akhirnya segmen AJ, JK, KL, LP, AM, MN, NC, CQ dan akhirnya PB ditarik.

Harus diperhatikan bahawa kaedah pembinaan tidak sepenuhnya tepat, kerana dapat disahkan bahwa sisi PB terakhir adalah 0.7% lebih lama daripada sisi lain. Sehingga kini, kaedah pembinaan dan pembinaan kompas tidak diketahui 100% tepat.

Contoh

Beberapa contoh yang diselesaikan akan ditangani di bawah.

Contoh 1

Anda mahu membina enegon biasa yang mengukur 2 cm. Radio apa yang sepatutnya lilitan yang dibentangkannya, sehingga apabila menerapkan pembinaan yang telah diterangkan sebelumnya, hasil yang diinginkan diperolehi?

Penyelesaian:

Dalam seksyen terdahulu, formula yang mengaitkan radius r lilitan yang dilampirkan dengan d dégon biasa disimpulkan:

D = 2r cos (70º)

Membersihkan r dari ungkapan sebelumnya yang kita ada:

R = d / (2 cos (70º)) = 1,4619 * d

Menggantikan nilai d = 2 cm dalam formula sebelumnya jejari 2.92 cm diperolehi.

Contoh 2

Berapa kawasan enegon sampingan 2 cm biasa?

Penyelesaian:

Untuk menjawab soalan ini, anda perlu merujuk kepada formula, yang sebelum ini ditunjukkan, yang membolehkan anda mencari kawasan enegon yang diketahui panjang d di sisinya:

Kawasan Enegon = (9/4) d² Tan (70º) = 6,1818 d²

Menggantikan d untuk nilai 2 cm dalam formula anterior diperoleh:

Kawasan Enegon = 24.72 cm

Rujukan

1. C. Dan. Ke. (2003). Elemen Geometri: Dengan Latihan dan Geometri Kompas. Universiti Medellin.
2. Campos, f., Cerecedo, f. J. (2014). Matematik 2. Kumpulan Editorial Patria.
3. Dibebaskan, k. (2007). Cari poligon. Syarikat Pendidikan Benchmark.
4. Hendrik, v. (2013). Poligon umum. Birkhäuser.
5. Iger. (s.F.). Matematik semester pertama Tacaná. Iger.
6. Jr. Geometri. (2014). Poligon. Lulu Press, Inc.
7. Miller, Heeren, & Hornsby. (2006). Matematik: Penalaran dan Aplikasi (Edisi Kesepuluh). Pendidikan Pearson.
8. Patiño, m. (2006). Matematik 5. Progreso editorial.