Formula ralat rawak dan persamaan, pengiraan, contoh, latihan

Dia ralat rawak jumlah fizikal terdiri daripada variasi yang tidak dapat diprediksi ukuran jumlah itu. Variasi ini boleh dihasilkan oleh fenomena yang diukur, oleh instrumen pengukur atau oleh pemerhati itu sendiri.

Kesalahan sedemikian tidak disebabkan oleh fakta bahawa sesuatu telah dilakukan salah semasa percubaan, tetapi itu adalah kesilapan yang wujud dalam proses pengukuran atau fenomena yang dikaji. Ini menyebabkan ukuran yang diukur kadang -kadang sedikit lebih besar dan kadang -kadang sedikit lebih rendah, tetapi biasanya berayun di sekitar nilai pusat.

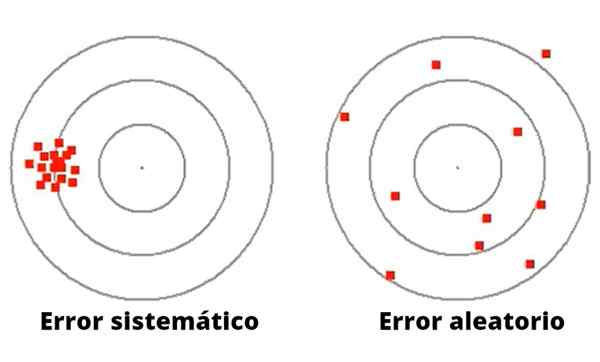
Rajah 1- Kesilapan rawak bervariasi dalam magnitud dan arah. Sebaliknya, kesilapan sistematik cenderung konsisten.

Tidak seperti ralat rawak, kesilapan sistematik boleh disebabkan oleh penentukuran buruk atau faktor skala yang tidak sesuai dalam instrumen pengukuran, termasuk kegagalan dalam peralatan eksperimen, atau pemerhatian yang tidak sesuai, yang menyebabkan sisihan dalam erti kata yang sama.

Rajah 1 menggambarkan perbezaan antara ralat sistematik dan rawak dalam permainan pelancaran dart ke sasaran dengan bulatan.

Sekiranya kiri, anak panah tertumpu di sekitar pusat. Pitcher anak panah ini, walaupun matlamat yang baik, mempunyai kegagalan sistematik, mungkin asal visual, atau dalam cara membuang.

Sebaliknya, periuk di sebelah kanan (dalam Rajah 1) mempunyai penyebaran yang hebat di sekitar sasaran pusat, oleh itu ia adalah periuk yang sangat tidak tepat, dengan matlamat yang buruk, yang secara sukarela membuat kesilapan rawak.

[TOC]

Formula dan persamaan dalam ralat rawak

Apabila proses pengukuran menunjukkan ralat rawak, perlu.

Sudah tentu, dalam setiap pengukuran adalah perlu untuk menjaga bahawa syarat -syarat di mana mereka dijalankan selalu sama.

Boleh melayani anda: Undang -undang Faraday: Formula, Unit, Eksperimen, Latihan,

Katakan pengukuran diulang n kali. Kerana terdapat ralat rawak dalam setiap pengukuran akan ada nilai yang sedikit berbeza. Katakan set n Pengukuran adalah:

x₁, x₂, x₃,..., x_n

Oleh itu, laporan nilai untuk ukuran? 

Nilai purata dan sisihan piawai

The nilai pertengahan Sama ada purata daripada set langkah, yang kami nyatakan dan dikira seperti berikut:

= (x₁ + x₂ + x₃ +... +x_n) / n

Sisihan piawai

Walau bagaimanapun, keputusan ini mempunyai margin ralat yang diberikan oleh sisihan piawai. Untuk menentukannya, anda mesti terlebih dahulu mengetahui sisihan dan kemudian varians:

-Penyimpangan d_Yo  bahawa setiap nilai diukur mempunyai Xi Mengenai nilai purata ialah:

d_Yo = x_Yo -

Sekiranya purata penyimpangan dikira, ia akan diperoleh secara sistematik = 0, Memandangkan itu: 

= (d₁ + d₂ + d₃ +... +d_n) /n =

= [x₁ - ) + (x₂ - ) +... +(x_n - )]/n

= (x₁+ x₂ +... + x_n) / n - n / n = - = 0

-Purata penyimpangan tidak berguna untuk mengetahui penyebaran langkah -langkah. Sebaliknya, nilai purata kuadrat penyimpangan atau varians, dilambangkan oleh σ², Ya betul.

Ia dikira mengikut formula berikut:

σ² = (d₁² + d₂² +… .+ d_n² ) / (N -1)

Dalam statistik jumlah ini dipanggil varians.  

Dan pada akar kuadrat varians yang dikenali sebagai Sisihan piawai σ:

σ = √ [(d₁² + d₂² +… .+ d_n² ) / (n -1)] 

Penyimpangan piawai σ menunjukkan bahawa:

1.- 68% daripada pengukuran yang dibuat dimasukkan dalam selang waktu [ - σ, + σ]. 

2.- 95% pengukuran berada dalam selang waktu [ - 2σ, + 2σ].

3.- 99.7% daripada langkah -langkah yang diambil dalam julat [ - 3σ, + 3σ].

Cara mengira ralat rawak?

Hasil pengukuran adalah nilai pertengahan daripada n Pengukuran yang dilambangkan dan dikira mengikut formula berikut:

Boleh melayani anda: kelajuan isolar: bagaimana ia dikira dan diselesaikan latihan

= (Σx_Yo) / n

Walau bagaimanapun, ia bukan nilai "tepat" pengukuran, kerana ia dipengaruhi oleh Ralat rawak ε, yang dikira seperti ini:

ε = σ / √n

Di mana:

σ = √ [(Σ (xi -)² ) / (n -1)]

Hasil akhir pengukuran mesti dilaporkan dalam mana -mana cara berikut:

1. ± σ / √n = ± ε Dengan tahap keyakinan 68%.
2. ± 2σ / √n = ± 2ε Dengan tahap keyakinan 95%.
3. ± 3σ / √n = ± 3ε Dengan tahap keyakinan 99.7%.

Kesalahan rawak mempengaruhi angka penting pengukuran yang terakhir, yang biasanya bertepatan dengan penghargaan instrumen pengukuran. Walau bagaimanapun, jika ralat rawak sangat besar, dua digit yang terakhir boleh dipengaruhi oleh variasi.

Contoh ralat rawak

Kesalahan rawak mungkin muncul dalam pelbagai kes di mana ukuran dibuat:

Mengukur panjang dengan ukuran pita atau peraturan

Apabila panjang diukur dengan peraturan atau ukuran pita dan bacaan jatuh antara jenama skala, maka nilai perantaraan itu dianggarkan.

Kadang -kadang anggaran mempunyai kelebihan dan kecacatan lain, jadi ralat rawak diperkenalkan ke dalam proses pengukuran.

Rajah 2. Kesalahan rawak mungkin muncul apabila panjang diukur dengan pita pita. Sumber: Pikrepo.

Kelajuan angin

Dalam pengukuran kelajuan angin mungkin ada perubahan dalam bacaan dari satu saat ke yang lain, disebabkan perubahan sifat fenomena.

Semasa membaca kelantangan dalam silinder lulus

Apabila kelantangan dibaca dengan silinder lulus, malah cuba meminimumkan kesilapan paralage, setiap kali ia diukur, sudut pemerhatian meniscal berubah sedikit, itulah sebabnya langkah -langkah yang dipengaruhi oleh ralat rawak.

Ia boleh melayani anda: Keadaan Keseimbangan Pertama: Penjelasan, Contoh, Latihan Rajah 3.- Di makmal kimia, ada kemungkinan untuk membuat kesilapan rawak dalam membaca silinder siswazah. Sumber: Pexels.

Apabila kedudukan anak diukur

Dengan mengukur ketinggian kanak -kanak, terutama jika ia agak gelisah, ia membuat perubahan postur kecil sedikit mengubah bacaan.

Semasa menggunakan skala bilik mandi

Apabila kita mahu mengukur berat badan kita dengan bilik mandi, perubahan kecil di titik sokongan, walaupun perubahan kedudukan dapat secara rawak mempengaruhi pengukuran.

Latihan diselesaikan

Kereta dorong mainan dibenarkan untuk melancarkan trek lurus dan cenderung dan diukur dengan jam randik masa yang mengambil seluruh trek. 

Pengukuran dilakukan 11 kali, dengan penjagaan melepaskan kereta dari tempat yang sama, tanpa memberi impuls dan menjaga kecenderungan membetulkan.

Set hasil yang diperoleh ialah:

3,12S 3.09S 3.04S 3.04S 3.10S 3.08S 3.05S 3.10s 3.11s 3.06s, 3.03s

Apakah ralat rawak langkah -langkah?

Rajah 4. Mengambil masa mainan mainan yang turun melalui pesawat yang cenderung. Sumber: Fanny Zapata.

Penyelesaian

Seperti yang dapat dilihat, hasil yang diperoleh tidak unik dan berbeza sedikit.

Yang pertama adalah untuk mengira nilai masa keturunan purata, memperoleh 3.074545455 saat.

Tidak masuk akal untuk mengekalkan begitu banyak perpuluhan, kerana setiap pengukuran mempunyai tiga angka penting dan perpuluhan kedua setiap langkah tidak pasti, kerana ia adalah batas penghargaan randik, oleh itu hasilnya dibulatkan kepada dua perpuluhan:

= 3.08 s.

Dengan kalkulator dalam mod statistik, sisihan piawai adalah σ = 0.03 s Dan ralat standard adalah σ / √11 = 0.01 s. Hasil akhir dinyatakan seperti berikut:

Masa keturunan 

3.08 s ± 0.01s (dengan tahap keyakinan 68%)

3.08 s ± 0.02S (dengan tahap keyakinan 95%)

3.08 s ± 0.03s (dengan tahap keyakinan 99.7%)

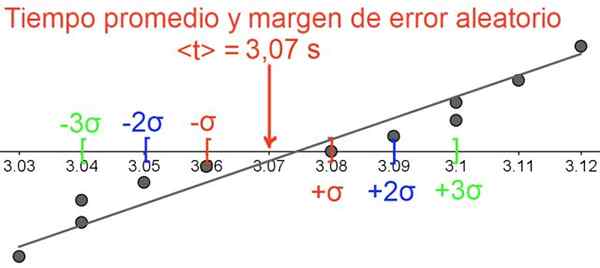Rajah 5. Margin ralat rawak, ambil perhatian bahawa data dikumpulkan sekitar nilai purata. Sumber: f. Zapata.

Rujukan

1. Canavos, g. 1988. Kebarangkalian dan Statistik: Aplikasi dan Kaedah. McGraw Hill.
2. DEVORE, J. 2012. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Ke -8. Edisi. Cengage.
3. Helmestine a. Kesalahan rawak Vs. Kesalahan sistematik. Pulih dari: Thoughtco.com
4. Laredo, e. Kesalahan tengah. Pulih dari: USB.Pergi.
5. Levin, r. 1988. Statistik untuk pentadbir. 2. Edisi. Prentice Hall.