Fungsi trigonometri songsang, diperolehi, contoh, latihan

The Fungsi trigonometri songsang, Seperti namanya, mereka adalah fungsi songsang yang sepadan dengan fungsi sinus, kosinus, tangen, cotangen, pengeringan dan penuai.

Fungsi trigonometri songsang dilambangkan dengan nama yang sama fungsi trigonometrik langsung yang sesuai ditambah dengan awalan Arka. Oleh itu:

1.- Arcsen (x) Ia adalah fungsi trigonometri songsang fungsi dosa (x)

2.- Arccos (x) Ia adalah fungsi trigonometri songsang fungsi cos (x)

3.- Arctan (x) Ia adalah fungsi trigonometri songsang fungsi Tan (x)

4.- Arccot ​​(x) Ia adalah fungsi trigonometri songsang fungsi Cot (x)

5.- Arcsec (x) Ia adalah fungsi trigonometri songsang fungsi sec (x)

6.- ARCCSC (x) Ia adalah fungsi trigonometri songsang fungsi CSC (x)

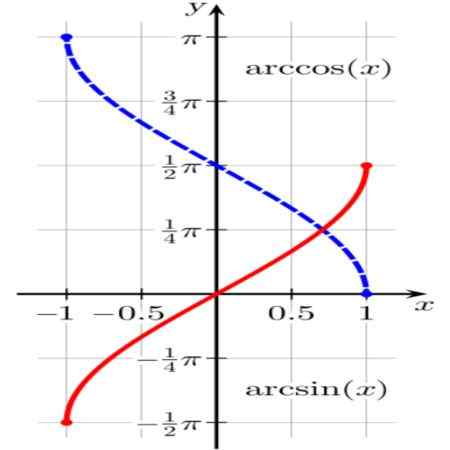
Rajah 1. Fungsi Arcsen (x) (dalam warna merah) dan arccos (x) (berwarna biru). Sumber: Wikimedia Commons.

Fungsinya θ = arcsen (x) Ia menghasilkan arka unit θ (atau sudut dalam radian θ) seperti itu dosa (θ) = x.

Oleh itu, sebagai contoh, arcsen (√3/2) = π/3 Oleh kerana seperti yang diketahui, payudara π/3 radians sama dengan √3/2.

[TOC]

Nilai utama fungsi trigonometri songsang

Supaya fungsi matematik f (x) mempunyai songsang g (x) = f^-1(x) perlu fungsi ini Injective, Yang bermaksud bahawa setiap nilai dan set ketibaan fungsi f (x) berasal dari satu dan hanya nilai x.

Jelas bahawa keperluan ini tidak dipenuhi oleh sebarang fungsi trigonometri. Untuk menjelaskan perkara itu, mari kita perhatikan bahawa nilai y = 0.5 boleh diperolehi dari fungsi sinus dengan cara berikut:

• dosa (π/6) = 0.5
• dosa (5π/6) = 0.5
• dosa (7π/6) = 0.5

Dan banyak lagi, kerana fungsi sinus berkala dengan tempoh 2π.

Ia dapat melayani anda: gandaan 8: Apa dan penjelasan

Untuk menentukan fungsi trigonometri songsang, perlu menyekat domain fungsi trigonometri langsung mereka, sehingga mereka memenuhi keperluan suntikan.

Domain terhad fungsi langsung ini akan menjadi julat utama atau cawangan fungsi songsang yang sepadan.

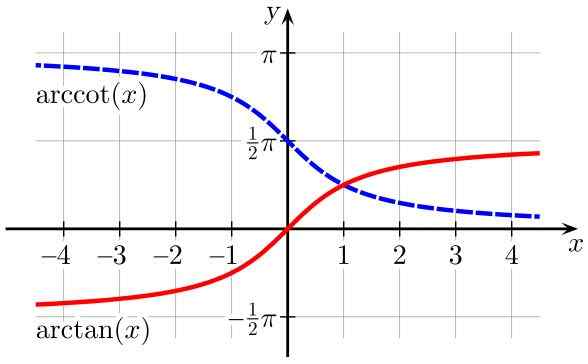Rajah 2. Fungsi Arctan (x) (dalam warna merah) dan arccot ​​(x) (berwarna biru). Sumber: Wikimedia Commons.

Jadual domain dan julat fungsi trigonometri songsang

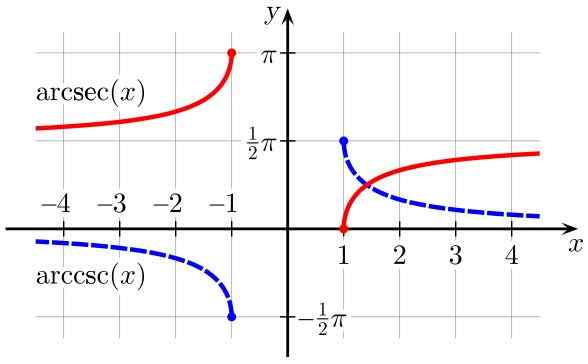Rajah 3. Arcsec (x) (dalam merah) dan arccsc (x) (dalam biru) fungsi (berwarna biru). Sumber: Wikimedia Commons.

Berasal dari fungsi trigonometri songsang

Untuk mendapatkan derivatif fungsi trigonometri songsang, sifat -sifat derivatif digunakan, khususnya yang diperoleh dari fungsi songsang.

Jika kita menunjukkan f (y) ke fungsi dan oleh f^-1(x) Kepada fungsi songsangnya, maka yang diperoleh dari fungsi terbalik berkaitan dengan derivatif fungsi langsung melalui hubungan berikut:

[F^-1(x)] '= 1/ f' [f^-1(x)]

Contohnya: jika x = f (y) = √y adalah fungsi langsung, songsangnya akan

y = f^-1(x) = x². Marilah kita memohon peraturan terbalik terbalik kepada kes mudah ini untuk melihat bahawa peraturan ini dipenuhi:

[x²] '= 1 / [√y]' = 1 / (½ dan^-½ = 2 dan^½ = 2 (x²)^½ = 2x 

Nah, kita dapat menilai helah ini untuk mencari yang diperoleh dari fungsi trigonometri songsang.

Contohnya, kami mengambil θ = arcsen (x) Sebagai fungsi langsung, maka fungsi songsangnya akan dosa (θ) = x.

[Arcsen (x)] '= 1 / [sin (θ)]' = 1 / cos (θ) = 1 / √ (1 - sen (θ)²) = ..

... = 1 / √ (1 - x²) .

Dengan cara ini, semua yang berasal dari fungsi trigonometri songsang boleh diperolehi, yang ditunjukkan di bawah:

Rajah 4. Jadual yang diperoleh dari fungsi trigonometri songsang. Sumber: Wikimedia Commons.

Derivatif ini sah untuk sebarang argumen z yang dimiliki oleh nombor kompleks dan oleh itu juga sah untuk sebarang hujah sebenar x, kerana z = x + 0i.

Boleh melayani anda: Quadrilateral: Unsur, sifat, klasifikasi, contoh

Contoh

- Contoh 1

Cari Arctan (1).

Penyelesaian

Arctan (1) adalah arka unit (sudut dalam radian) ፀ sehingga tan (ፀ) = 1. Sudut itu ፀ = π/4 kerana SO (π/4) = 1. Kemudian Arctan (1) = π/4.

- Contoh 2

Hitung arcsen (cos (π/3)).

Penyelesaian

Sudut π/3 radians adalah sudut yang ketara yang kosinusnya ½, sehingga masalahnya dikurangkan untuk mencari arcsen (½).

Oleh itu, ini mengenai mencari sudut yang memberi sinus ½. Sudut itu π/6, kerana sen (π/6) = sen (30º) = ½. Oleh itu arcsen (cos (π/3)) = π/6. 

Latihan

- Latihan 1

Cari hasil ungkapan berikut:

Sec (Arcan (3)) + CSC (Arccot ​​(4))

Penyelesaian

Kami mula menamakan α = arcan (3) dan β = arcot (4). Jadi ungkapan yang perlu kita hitung adalah seperti ini:

Sec (α) + CSC (β)

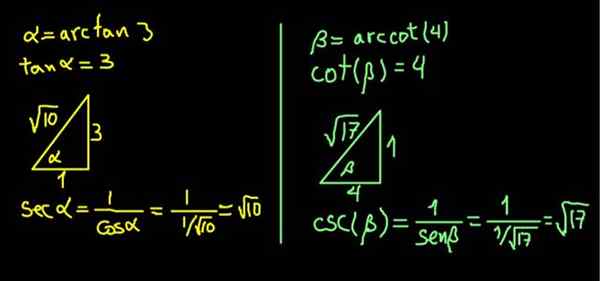
Ekspresi α = Arcan (3) bersamaan dengan mengatakan SO (α) = 3.

Oleh kerana tangen adalah kaki yang bertentangan di sebelah bersebelahan, segitiga segi empat tepat Cateto menentang α daripada 3 unit dan kategori bersebelahan 1 unit dibina, supaya SO (α) = 3/1 = 3.

Dalam segitiga segi empat tepat, hipotenus ditentukan oleh teorem pythagoras. Dengan nilai -nilai ini, √10, supaya:

Sec (α) = Hypotenuse / Cateto bersebelahan = √10 / 1 = √10.

Begitu juga β = arcot (4) bersamaan dengan menyatakan bahawa Cot (β) = 4.

Segitiga segi empat tepat Cateto bersebelahan dengan β 4 unit dan Cateto yang bertentangan dengan 1 unit dibina, supaya Cot (β) = 4/1.

Segitiga segera selesai mencari hipotenanya terima kasih kepada teorem Pythagoras. Dalam kes ini ternyata mempunyai unit √17. Kemudian CSC (β) = Hypotenuse / bertentangan Cateto = √17 / 1 = √17 dikira.

Ia boleh melayani anda: tempoh fungsi y = 3sen (4x)

Ingat bahawa ungkapan yang mesti kita hitung adalah: 

Sec (Arcan (3)) + CSC (Arcot (4)) = SEC (α) + CSC (β) = ..

... = √10 + √17 = 3.16 + 4.12 = 7,28.

- Latihan 2

Cari penyelesaian:

Cos (2x) = 1 - sen (x)

Penyelesaian

Adalah perlu bahawa semua fungsi trigonometri dinyatakan dalam hujah atau sudut yang sama. Kami akan menggunakan identiti sudut berganda:

Cos (2x) = 1 - 2 sen²(x)

Kemudian ungkapan asal dikurangkan ke:

1 - 2 Sen²(x) = 1 - dosa x

Setelah dipermudahkan dan difungsikan, ia dinyatakan sebagai:

dosa (x) (2 sen (x) - 1) = 0

Yang menimbulkan dua persamaan yang mungkin: dosa (x) = 0 dengan penyelesaian x = 0 dan persamaan lain sen (x) = ½ dengan x = π/6 sebagai penyelesaian.

Penyelesaian kepada persamaan yang dibangkitkan adalah: x = 0 atau x = π/6.

- Latihan 3

Cari penyelesaian persamaan trigonometri berikut:

cos (x) = dosa²(x)

Penyelesaian

Untuk menyelesaikan persamaan ini, adalah mudah untuk meletakkan satu jenis fungsi trigonometri, jadi kami akan menggunakan identiti trigonometri asas supaya persamaan asal ditulis semula seperti berikut:

cos (x) = 1 - cos²(x)

Jika kita namakan y = cos (x), ungkapan boleh ditulis semula sebagai:

dan² + dan - 1 = 0

Ia adalah persamaan darjah kedua dalam dan, penyelesaiannya:

y = (-1 ± √5) / 2

Maka nilai x yang memenuhi persamaan asal adalah:

x = arcos ((-1 ± √5) / 2)

Penyelesaian sebenar menjadi tanda positif x = 0.9046 rad = 51.83º.

Penyelesaian lain adalah kompleks: x = (π - 1.06 i) rad.

Rujukan

1. Hazewinkel, m. 1994. Encyclopaedia of Mathematics. Penerbit Akademik Kluwer / Springer Science & Business Media. 
2. Pasangan mudah alih. Fungsi trigonometri songsang. Pulih dari: Matemovil.com
3. Formula Universe. Fungsi trigonometri songsang. Pulih dari: universoformulas.com
4. Weisstein, Eric W. Mencipta fungsi trigonometri. Pulih dari: Mathworld.Wolfram.com
5. Wikipedia. Mencipta fungsi trigonometri. Diperoleh dari: dalam.Wikipedia.com