Ralat Anggaran Standard Bagaimana dikira, contoh, latihan

Dia Kesalahan anggaran standard Mengukur sisihan dalam nilai populasi sampel. Iaitu, ralat anggaran standard mengukur kemungkinan variasi sampel yang mungkin berkenaan dengan nilai sebenar purata penduduk.

Sebagai contoh, jika anda ingin mengetahui usia purata penduduk negara (maksud penduduk) sekumpulan kecil penduduk diambil, yang akan kita panggil "menunjukkan". Daripadanya umur purata (min sampel) diekstrak dan diandaikan bahawa penduduk mempunyai umur purata dengan ralat anggaran standard yang berbeza -beza lebih kurang.

M. W. Toews [CC oleh 2.5 (https: // creativeCommons.Org/lesen/by/2.5)]

Harus diingat bahawa penting untuk tidak mengelirukan sisihan piawai dengan ralat standard dan ralat anggaran standard:

1- Penyimpangan piawai adalah ukuran penyebaran data; iaitu, ia adalah ukuran kebolehubahan penduduk.

2- Kesalahan standard adalah ukuran kebolehubahan sampel, dikira berdasarkan sisihan piawai penduduk.

3- Ralat Anggaran Standard adalah ukuran kesilapan yang dibuat ketika mengambil sampel min sebagai anggaran penduduk maksudnya.

[TOC]

Bagaimana ia dikira?

Kesalahan anggaran standard boleh dikira untuk semua langkah yang diperolehi dalam sampel (contohnya, ralat anggaran purata standard atau kesilapan standard anggaran sisihan piawai) dan mengukur kesilapan yang dibuat apabila menganggarkan ukuran populasi yang benar dari nilai sampelnya

Dari ralat anggaran standard, selang keyakinan langkah yang sepadan dibina.

Boleh melayani anda: matriks terbalik: pengiraan dan senaman diselesaikan

Struktur umum formula untuk ralat anggaran standard adalah seperti berikut:

Ralat Anggaran Standard = ± pekali amanah * Kesalahan standard

Koefisien Amanah = Had Nilai Sampel Statistik atau Pengagihan Sampling (Normal atau Gauss Bell, Pelajar T, antara lain) untuk selang tertentu kebarangkalian.

Ralat standard = sisihan piawai penduduk dibahagikan dengan akar kuadrat saiz sampel.

Koefisien keyakinan menunjukkan jumlah kesilapan standard yang sanggup menambah dan menolak disesuaikan untuk mempunyai tahap keyakinan tertentu terhadap hasilnya.

Contoh pengiraan

Anggapkan bahawa anda cuba untuk menganggarkan perkadaran orang dalam populasi yang mempunyai tingkah laku A, dan anda ingin mempunyai keyakinan 95% terhadap hasilnya.

Sampel orang N diambil dan bahagian sampel p dan pelengkapnya ditentukan.

Ralat Anggaran Standard (EEE) = ± pekali amanah * Kesalahan standard

Pekali amanah = z = 1.96.

Ralat standard = akar kuadrat sebab antara produk perkadaran sampel untuk pelengkapnya dan saiz sampel n.

Dari kesilapan anggaran standard, selang di mana perkadaran penduduk atau sampel sampel sampel lain yang boleh dibentuk dari populasi itu ditubuhkan, dengan tahap keyakinan 95%:

P -EEE ≤ Proporsi Penduduk ≤ P + EEE

Latihan yang diselesaikan

Latihan 1

1- Anggapkan bahawa anda cuba untuk menganggarkan perkadaran orang dalam populasi yang mempunyai keutamaan untuk formula tenusu yang diperkaya, dan anda ingin mempunyai keyakinan 95% dalam hasilnya.

Boleh melayani anda: bahagian sintetik

Sampel sebanyak 800 orang diambil dan ditentukan bahawa 560 orang dalam sampel mempunyai keutamaan untuk formula tenusu diperkaya. Tentukan selang di mana perkadaran penduduk boleh dijangkakan dan perkadaran sampel lain yang boleh diambil dari penduduk, dengan keyakinan 95%

a) Mari kita hitung bahagian sampel p dan pelengkapnya:

P = 560/800 = 0.70

Q = 1 -p = 1 -0.70 = 0.30

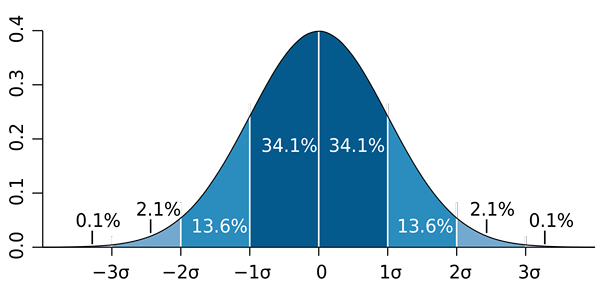
b) diketahui bahawa perkadaran mendekati taburan normal kepada sampel saiz yang besar (lebih besar daripada 30). Kemudian, Peraturan 68 - 95 - 99 yang diterapkan.7 Dan anda mesti:

Pekali amanah = z = 1.96

Ralat standard = √ (p*q/n)

Ralat Anggaran Standard (EEE) = ± (1.96)*√ (0.70)*(0.30)/800) = ± 0.0318

c) Dari kesilapan anggaran standard, selang di mana perkadaran penduduk dijangka dengan tahap keyakinan 95% ditubuhkan:

0.70 -0.0318 ≤ Proporsi Penduduk ≤ 0.70 + 0.0318

0.6682 ≤ Proporsi Penduduk ≤ 0.7318

Anda boleh mengharapkan bahagian sampel 70% untuk berubah sehingga 3.18 mata peratusan jika mengambil sampel yang berbeza sebanyak 800 individu atau bahawa bahagian sebenar penduduk adalah antara 70 - 3.18 = 66.82% dan 70 + 3.18 = 73.18%.

Latihan 2

2- Kami akan mengambil dari Spiegel dan Stephens, 2008, kajian kes berikut:

Daripada jumlah gred matematik pelajar pertama di universiti, sampel rawak sebanyak 50 kelayakan diambil di mana purata yang dijumpai adalah 75 mata dan sisihan piawai, 10 mata. Apakah had keyakinan 95% untuk menganggarkan purata kelayakan matematik universiti?

Ia dapat melayani anda: apakah hubungan antara kawasan rhombus dan segi empat tepat?

a) Mari kita mengira ralat anggaran standard:

Pekali keyakinan 95%= z = 1.96

Ralat standard = s/√n

Ralat Anggaran Standard (EEE) = ± (1.96)*(10√50) = ± 2.7718

b) Dari kesilapan anggaran standard, selang di mana populasi maksud atau purata sampel 50 yang lain ditubuhkan, dengan tahap keyakinan 95%:

50 -2.7718 ≤ Penduduk Purata ≤ 50 + 2.7718

47.2282 ≤ Penduduk Purata ≤ 52.7718

c) Anda boleh mengharapkan purata sampel berubah sehingga 2.7718 Mata Jika sampel berbeza 50 gred diambil atau purata sebenar gred matematik penduduk universiti adalah antara 47.2282 mata dan 52.7718 mata.

Rujukan

1. Abraira, v. (2002). Sisihan piawai dan ralat standard. Majalah Semergen. Web pulih.Arkib.org.
2. Rumsey, d. (2007). Statistik pertengahan untuk patung. Wiley Publishing, Inc.
3. Salinas, h. (2010). Statistik dan kebarangkalian. Pulih dari tikar.Uda.Cl.
4. Sokal, r.; Rohlf, f. (2000). Biometri. Prinsip dan Amalan Statistik dalam Penyelidikan Biologi. Ketiga ed. Edisi Blume.
5. Spiegel, m.; Stephens, l. (2008). Statistik. Ed keempat. McGraw-Hill/Inter-American dari Mexico S. Ke.
6. Wikipedia. (2019). 68-95-99.7 Peraturan. Diambil dari.Wikipedia.org.
7. Wikipedia. (2019). Kesalahan biasa. Diambil dari.Wikipedia.org.