Penilaian fungsi

Untuk menilai fungsi yang mana gambarajah diketahui, untuk nilai tertentu atau elemen set permulaan, sudah cukup untuk memerhatikan elemen yang sepadan dalam set ketibaan. Sumber: f. Zapata.

Apakah penilaian fungsi?

The Penilaian fungsi Ia terdiri daripada menentukan imej nilai domain tertentu. Dengan kata lain, untuk nilai tertentu set permulaan, anda perlu mencari yang sepadan dengan set ketibaan.

Fungsi boleh diwakili dalam beberapa cara. Jika, sebagai contoh, gambarajah Venn tersedia, penilaiannya sangat mudah, sudah cukup untuk memilih elemen permulaan atau set domain, dan lihat elemen yang sepadan dengan set ketibaan.

Dalam "...... adalah gambarajah modal ...", diwakili di atas, ketika menilai fungsi ini dalam elemen "Kanada", ia adalah elemen "Ottawa", sekiranya berbuat demikian dengan "Mexico", ia adalah "Mexico City" dan Jadi pada.

Jika fungsi diberikan dalam bentuk pasangan kemas, penilaian juga mudah: ahli kedua tork teratur adalah imej ahli pertama. Sebagai contoh, dengan fungsi f (x) yang diterangkan oleh:

f (x) = (0.0); (1.2); (2,4); (3,6); (4.8); (5.10); (6,12)

Apabila menilai fungsi untuk nilai 3, hasilnya ialah 6; Semasa menilai selama 5, ia adalah 10 dan sebagainya.

Begitu juga, fungsi dapat dinilai apabila graf tersedia, dengan syarat nilai yang ingin anda nilai muncul di dalamnya.

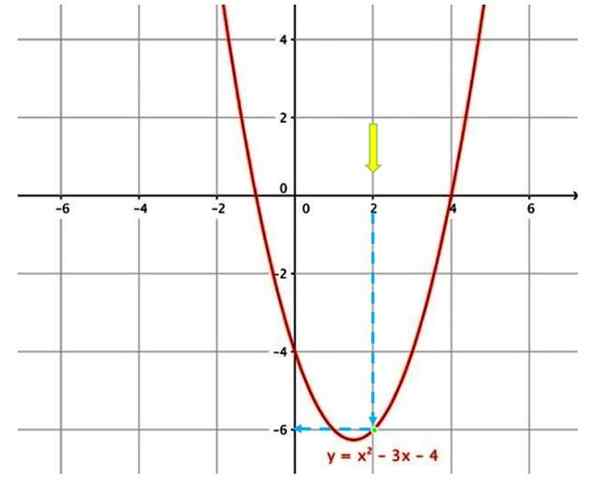Graf untuk menilai fungsi

Sebagai contoh, untuk menilai fungsi yang ditunjukkan di atas, pada x = 2, perkara pertama adalah mencari graf a x = 2 (anak panah kuning).

Kemudian, anda perlu bergerak mengikuti anak panah menegak biru, sehingga anda menyentuh lengkung (titik hijau). Ikuti anak panah biru sekali lagi, yang menunjukkan nilai yang sepadan pada paksi menegak, oleh itu, apabila menilai fungsi pada x = 2, y = -6 diperolehi.

Ia boleh melayani anda: Fungsi Trigonometrik: Asas, Dalam Plane Cartesian, Contoh, Latihan

Menilai fungsi tertentu dalam notasi matematik

Di bahagian bawah graf di atas, fungsi grafik muncul, tetapi diberikan dalam notasi matematik, iaitu, melalui formula:

f (x) = x² - 3x - 4

Apabila anda ingin menilai fungsi dalam sebarang nilai x = a, anda perlu mencari f (a), yang hanya dibaca "f dari".

Untuk mencari hasilnya, x = a digantikan dalam formula fungsi, dan operasi dan pengiraan yang diminta dijalankan di sana.

Katakan anda ingin menilai fungsi contoh di x = -1. Ini bermaksud bahawa f (-1) mesti dijumpai.

Langkah pertama ialah menggantikan x = -1 dalam fungsi:

F (-1) = (-1)² - 3 ∙ (-1) - 4

Dan kemudian, menjalankan operasi yang ditunjukkan, yang dalam contoh ini adalah:

• Cari kuadrat -1: (-1)² = 1
• Tolak nilai sebelumnya produk 3 ∙ (-1): 3 ∙ (-1) = -3
• Dari hasil sebelumnya, tolak 4

F (-1) = (-1)² - 3 ∙ (-1) - 4 = 1 + 3 - 4 = 0

Pembaca dapat menyokong hasil ini, dari graf fungsi.

Prosedur yang diterangkan boleh digunakan untuk menilai fungsi di mana -mana nilai domain lain. Sebagai contoh, anda boleh mencari f (-2), f (100) atau bahkan f (h), di mana h adalah nilai pembolehubah sewenang-wenangnya, yang dimiliki oleh domain fungsi.

Menilai fungsi pada nilai x = h 

Katakan anda ingin menilai fungsi pada beberapa nilai sewenang -wenangnya, operasi kerap dalam pengiraan matematik.

Dalam kes ini, x digantikan oleh H, dengan cara yang sama yang dilakukan apabila x mengambil nilai berangka, dan hasilnya dipermudahkan sebanyak mungkin.

Apabila operasi yang dihasilkan tidak lagi dapat dipermudahkan, operasi yang dihasilkan ditinggalkan.

Ia boleh melayani anda: Enegon: Properties, Cara Membuat Enegon, Contoh

Contoh

Anda ingin menilai fungsi f (x) = x² - 3x - 4 pada x = h+1. Pendekatan yang diperlukan adalah seperti berikut:

F (H+1) = (H+1)² - 3 ∙ (H+1) - 4

Di sebelah kanan kesamaan, istilah pertama adalah produk yang luar biasa:

(H+1)² = h² +2h + 1

Istilah berikut diselesaikan melalui harta pengedaran:

3 ∙ (H + 1) = 3H + 3

Semasa menggantikan semua perkara di atas, anda mempunyai:

F (H+1) = (H+1)² - 3 ∙ (H+1) - 4 = h² +2h + 1 - (3h + 3) - 4

Istilah yang sama dikurangkan, oleh jumlah algebra:

f (h+1) = h² + 2h + 1 - 3h - 3 - 4 = h² - H - 6

Kota pembezaan

Kota pembezaan atau nisbah perbezaan d fungsi f (x) ditakrifkan sebagai:

Dengan syarat h ≠ 0, yang diperlukan, kerana pembahagian oleh 0 tidak ditakrifkan.

Kota ini ditafsirkan secara geometri sebagai cerun garis secant ke lengkung, iaitu garis yang melewati dua mata daripadanya. Koordinat titik ini adalah: [x, f (x)] dan [x+h; f (x+h)], seperti yang dilihat dalam angka berikut:

Kota pembezaan bersamaan dengan mengira cerun garis secant ke lengkung, yang melalui mata yang ditunjukkan. Sumber: Wikimedia Commons.

Itulah sebabnya kota ini muncul dalam pengiraan derivatif fungsi, kerana membuat "H" mendekati nilai 0, garis secant cenderung menjadi garis tangen pada titik (x, y), kerana titik -titik dalam persimpangan persimpangan angka itu sangat dekat sehingga mereka cenderung ke titik yang sama.

Oleh itu, garis menjadi tangen (memintas lengkung dalam satu titik).

Ini adalah definisi yang diperoleh dari fungsi: cerun garis tangen ke lengkung dalam titik koordinat (x, f (x))).

Ia boleh melayani anda: media berwajaran: bagaimana ia dikira, contoh dan latihan

Seperti yang dapat dilihat, quotient pembezaan memerlukan menilai fungsi dalam (x + h) dan dalam x. Contoh berikut menggambarkan cara melakukannya.

Contoh 1

Anda ingin mencari pembezaan fungsi f (x) = 2x - 3. Langkah pertama adalah untuk meningkatkan penilaian fungsi untuk x = x + h, seperti ini:

f (x+h) = 2 ∙ (x+h) - 3 = 2x+2h - 3

Kemudian, hasilnya digantikan dalam definisi d, yang diberikan sebelumnya:

Dengan h ≠ 0.

Pengangka dipermudahkan sejauh mungkin, mengurangkan istilah yang serupa:

Akhirnya, faktor umum dalam pengangka dan penyebut dipermudahkan:

D = 2

Contoh 2

Cari pembezaan fungsi f (x) = x² - 3x - 4.

Kami meneruskan seperti dalam contoh sebelumnya, mencari f (x+h) yang pertama, menggantikan hasil dalam d dan memudahkan maksimum:

f (x+h) = (x+h)² - 3 (x+h) - 4 = x² + 2HX + H² - 3x - 3h - 4

= 2x+H-3

Oleh itu:

D = 2x+H-3

Di mana h ≠ 0.

Latihan yang diselesaikan

Latihan 1

Menilai fungsi f (x) = 2x² - 4x + 1 Bila:

a) x = -1
b) x = 0
c) x = 2

Penyelesaian kepada

F (-1) = 2 (-1)² - 4 (-1) + 1 = 2 + 4 + 1 = 7

Penyelesaian b

F (0) = 2 (0)² - 4 (0) + 1 = 0 - 0 + 1 = 1

Penyelesaian c

F (2) = 2 ∙ 2² - 4 ∙ 2 + 1 = 8 - 8 + 1 = 1

Latihan 2

Pasukan pemuliharaan menentukan bahawa fungsi w (t) = 0.Lt² + 1.8t berfungsi untuk memodelkan jumlah sisa "w", dalam kilogram, yang dibuang ke dalam sungai tertentu, dalam masa "t", yang diberikan dalam beberapa hari.

Kirakan jumlah sisa yang dibuang ke dalam sungai di akhir:

a) 3 hari
b) 1 minggu
c) 1 bulan

Penyelesaian kepada

Fungsi W (t) dinilai pada t = 3 hari:

W (3) = 0.1 × 3² +1.8 × 3 = 0.9 + 5.4 = 6.3 kilogram

Penyelesaian b

Sebelum menilai, anda perlu menghabiskan 1 minggu hingga hari:

1 minggu = 7 hari

W (7) = 0.1 × 7² +1.8 × 7 = 4.9 + 12.6 = 17.5 kilogram

Penyelesaian c

Sekali lagi, perlu mengubah bulan ke hari:

1 bulan = 30 hari

W (30) = 0.1 × 30² +1.8 × 30 = 90 + 54 = 144 kilogram

Rujukan

1. Larson, r. 2012. Precalculation. Ke -8. Edisi. Pembelajaran Cengage.
2. Institut Monterey. Menilai fungsi. Pulih dari: Montereyinstitute.org.
3. Stewart, J. 2007. Preccculment: Matematik untuk Pengiraan. 5th. Edisi. Pembelajaran Cengage.
4. Sullivan, m. 1997. Precalculation. Ke -4. Edisi. Pendidikan Pearson.
5. Zill, d. 2008. Preccculment dengan kemajuan pengiraan. Ke -4. Edisi. McGraw Hill.