Pemfaktoran

Apakah pemfaktorannya?

Pemfaktoran adalah kaedah di mana polinomial dinyatakan dalam bentuk pendaraban faktor, yang boleh menjadi nombor, huruf atau kedua -duanya. Untuk faktor, faktor -faktor yang biasa dengan istilah dikumpulkan, dan dengan cara ini polinomial dibusuk dalam beberapa polinomial.

Oleh itu, apabila faktor berlipat ganda antara satu sama lain, hasilnya adalah polinomial asal. Pemfaktoran adalah kaedah yang sangat berguna apabila terdapat ungkapan algebra, kerana ia boleh menjadi pendaraban beberapa istilah mudah; Contohnya: ke -2² + 2ab = 2a _* (A + b).

Terdapat kes -kes di mana polinomial tidak boleh dipertimbangkan kerana tidak ada faktor yang sama di antara istilahnya; Oleh itu, ungkapan algebra ini hanya dapat dibahagikan antara mereka dan oleh 1. Contohnya: x + y + z.

Dalam ungkapan algebra, faktor umum adalah pembahagi umum maksimum istilah yang mengarangnya.

Kaedah pemfaktoran

Terdapat beberapa kaedah pemfaktoran, yang digunakan bergantung pada kes itu. Sebahagian daripada ini adalah perkara berikut:

Pemfaktoran umum

Dalam kaedah ini faktor -faktor yang biasa dikenalpasti; iaitu, mereka yang diulang dari syarat ungkapan. Kemudian harta pengedaran digunakan, pembahagi umum maksimum dikeluarkan dan pemfaktoran selesai.

Dalam erti kata lain, faktor umum ungkapan dikenalpasti dan setiap istilah dibahagikan antara ini; Istilah yang dihasilkan akan didarabkan oleh pembahagi umum maksimum untuk menyatakan pemfaktoran.

Contoh 1

Faktor (b²x) + (b²dan).

Penyelesaian

Pertama adalah faktor umum setiap istilah, yang dalam kes ini adalah b², Dan kemudian istilah dibahagikan antara faktor umum seperti berikut:

(b²x) / b² = x

(b²y) / b² = y.

Pemfaktoran dinyatakan, mendarabkan faktor umum dengan istilah yang dihasilkan:

(b²x) + (b²y) = b² (x + y).

Contoh 2

Faktor (ke -2²b³) + (3ab²).

Penyelesaian

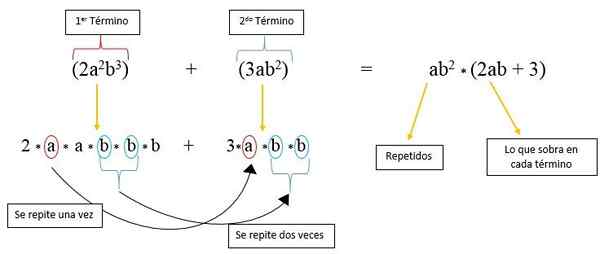
Dalam kes ini kita mempunyai dua faktor yang diulang dalam setiap istilah yang "A" dan "B", dan yang dibesarkan dengan kuasa. Untuk mempraktikkannya terlebih dahulu, kedua -dua istilah itu dipecahkan dalam bentuk panjang mereka:

2_*ke_*ke_*b_*b_*B + 3A_*b_*b

Ia dapat dilihat bahawa faktor "A" diulang hanya sekali dalam penggal kedua, dan faktor "B" diulang dua kali dalam hal ini; Jadi dalam istilah pertama hanya ada 2, faktor "a" dan satu "b"; Sementara dalam penggal kedua hanya 3 kekal.

Oleh itu, ia ditulis seberapa banyak kali sebagai "A" dan "B" diulang dan didarabkan oleh faktor -faktor yang tersisa dari setiap istilah, seperti yang diperhatikan dalam imej:

Pemfaktoran kumpulan

Seperti yang tidak dalam semua kes, pembahagi umum maksimum polinomial jelas dinyatakan, adalah perlu untuk membuat langkah -langkah lain untuk dapat menulis semula polinomial dan dengan demikian memberi gambaran.

Boleh melayani anda: Bahagian kerucut: Jenis, Aplikasi, Contoh

Salah satu langkah itu adalah untuk mengumpulkan syarat polinomial ke dalam beberapa kumpulan, dan kemudian menggunakan kaedah faktor umum.

Contoh 1

Faktor AC + BC + AD + BD.

Penyelesaian

Terdapat 4 faktor di mana dua adalah perkara biasa: dalam penggal pertama ia adalah "C" dan pada yang kedua adalah "D". Dengan cara itu kedua -dua istilah dikelompokkan dan berasingan:

(AC + BC) + (AD + BD).

Ia kini mungkin untuk menggunakan kaedah faktor yang sama, membahagikan setiap istilah dengan faktor umum dan kemudian mengalikan faktor yang sama dengan istilah yang dihasilkan, seperti ini:

(Ac + bc) / c = a + b

(ad + bd) / d = a + b

C (a + b) + d (a + b).

Sekarang binomial diperoleh yang biasa untuk kedua -dua istilah. Untuk faktornya didarabkan oleh faktor -faktor yang selebihnya; Dengan cara itu anda perlu:

AC + BC + AD + BD =  (C + d) _* (A + b).

Faktor Pemeriksaan

Kaedah ini digunakan untuk faktor polinomial kuadrat, juga dipanggil trinomial; iaitu, yang berstruktur sebagai kapak² ± bx + c, di mana nilai "a" berbeza dari 1. Kaedah ini juga digunakan apabila trinomial mempunyai bentuk x² ± bx + c dan nilai "a" = 1.

Contoh 1

Faktor x² + 5x + 6.

Penyelesaian

Anda mempunyai trinomial kuadratik bentuk x² ± bx + c. Untuk faktornya terlebih dahulu, dua nombor mesti dijumpai, apabila mengalikan, menghasilkan nilai "c" (iaitu, 6) dan jumlahnya sama dengan koefic "b". Nombor tersebut adalah 2 dan 3:

2 _* 3 = 6

2 + 3 = 5.

Dengan cara ini, ungkapan itu dipermudahkan seperti berikut:

(x² + 2x) + (3x + 6)

Setiap istilah adalah faktor:

• Untuk (x² + 2x) Istilah umum dikeluarkan: x (x + 2)
• Untuk (3x + 6) = 3 (x + 2)

Oleh itu, ungkapan itu tetap:

x (x +2) +3 (x +2).

Memandangkan anda mempunyai binomial yang sama, untuk mengurangkan ungkapan, ia melipatgandakan ini dengan istilah sisa dan ia harus:

x² + 5x + 6 = (x + 2) _* (x + 3).

Contoh 2

Faktor 4a² + 12a +9 = 0.

Penyelesaian

Anda mempunyai trinomial kuadratik bentuk kapak² ± bx + c dan untuk faktornya mengalikan semua ungkapan dengan pekali x²; Dalam kes ini, 4.

Ke -4² + 12a +9 = 0

Ke -4² (4) + 12a (4) + 9 (4) = 0 (4)

16 a² + 12a (4) + 36 = 0

4² ke² + 12a (4) + 36 = 0

Sekarang dua nombor mesti dijumpai, apabila mendarabkan antara satu sama lain, menghasilkan nilai "C" (iaitu 36) dan apabila menyertai pekali istilah "A", iaitu 6.

6 _* 6 = 36

6 + 6 = 12.

Dengan cara itu ungkapan ditulis semula, dengan mengambil kira bahawa 4² ke² = 4a _* Ke -4. Oleh itu, harta pengedaran digunakan untuk setiap istilah:

Boleh melayani anda: kotak mackinder

(4a + 6) _* (4a + 6).

Akhirnya, ungkapan dibahagikan dengan pekali a²; iaitu, 4:

(4a + 6) _* (4a + 6) / 4 = ((4a + 6) / 2) _* ((4a + 6)/ 2).

Ekspresi adalah seperti berikut:

Ke -4² + 12a +9 = (2a +3) _* (2a + 3).

Pemfaktoran dengan produk yang ketara

Terdapat kes -kes di mana, untuk benar -benar faktor polinomial dengan kaedah sebelumnya, ia menjadi proses yang sangat panjang.

Itulah sebabnya ungkapan dapat dibangunkan dengan formula produk yang ketara dan oleh itu proses menjadi lebih mudah. Antara produk terkenal yang paling banyak digunakan ialah:

• Perbezaan dua dataran: (a² - b²) = (a - b) _* (A + b)
• Persegi sempurna jumlah: a² + 2ab +b² = (a + b)²
• Persegi sempurna perbezaan: a² - 2ab + b² = (a - b)²
• Perbezaan dua kiub: a³ - b³ = (a-b)_*(Kepada² + ab + b²)
• Jumlah dua kiub: a³ - b³ = (a + b) _* (Kepada² - ab + b²)

Contoh 1

Faktor (5² - x²)

Penyelesaian

Dalam kes ini terdapat perbezaan dua dataran; Oleh itu, formula produk terkenal digunakan:

(Kepada² - b²) = (a - b) _* (A + b)

(5² - x²) = (5 - x) _* (5 + x)

Contoh 2

Faktor 16x² + 40x + 25²

Penyelesaian

Dalam kes ini, terdapat kuadrat sempurna dari jumlah, kerana dua istilah persegi dapat dikenalpasti, dan istilah yang tersisa adalah hasil dari mendarabkan dua oleh akar kuadrat istilah pertama, dengan akar kuadrat dari istilah kedua.

ke² + 2ab +b² = (a + b)²

Untuk faktor, hanya akar persegi istilah pertama dan ketiga dikira:

√ (16x²) = 4x

√ (25²) = 5.

Kemudian kedua -dua istilah yang dihasilkan dinyatakan dipisahkan oleh tanda operasi, dan semua polinomial persegi dinaikkan:

16x² + 40x + 25² = (4x + 5)².

Contoh 3

Faktor 27a³ - b³

Penyelesaian

Ekspresi mewakili penolakan di mana dua faktor ditinggikan ke kiub. Untuk memberi tumpuan kepada mereka, formula produk ketara perbezaan kiub digunakan, iaitu:

ke³ - b³ = (a-b)_*(Kepada² + ab + b²)

Oleh itu, kepada faktor, akar kubik dikeluarkan dari setiap istilah binomial dan didarabkan dengan kuadrat istilah pertama, ditambah dengan produk yang pertama dengan istilah kedua, ditambah dengan istilah kedua.

27a³ - b³

³√ (27a³) = 3a

³√ (-b³) = -b

27a³ - b³ = (3a - b) _* [(3a)² + 3ab + b²)]

27a³ - b³ = (3a - b) _* (9a² + 3ab + b²)

Pemfaktoran dengan peraturan ruffini

Kaedah ini digunakan apabila anda mempunyai polinomial darjah lebih besar daripada dua, untuk memudahkan ekspresi ke beberapa polinomial yang lebih kecil.

Contoh 1

Faktor q (x) = x⁴ - 9x² + 4x + 12

Penyelesaian

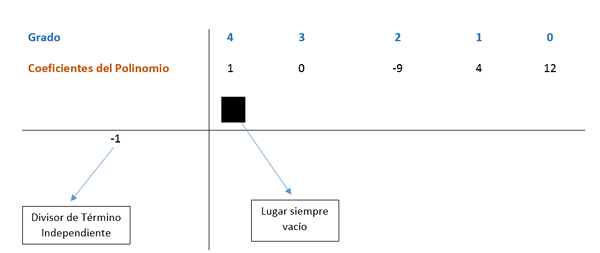
Pertama angka -angka yang menjadi pembahagi 12 dicari, iaitu istilah bebas; Ini adalah ± 1, ± 2, ± 3, ± 4, ± 6 dan ± 12.

Boleh melayani anda: gandaan 2: apa dan penjelasan

Kemudian x digantikan oleh nilai -nilai ini, dari yang paling sedikit hingga yang paling besar, dan oleh itu ditentukan dengan mana nilai -nilai pembahagian akan tepat; iaitu, selebihnya mestilah 0:

x = -1

Q (-1) = (-1)⁴ - 9 (-1)² + 4 (-1) + 12 = 0.

x = 1

Q (1) = 1⁴ - 9 (1)² + 4 (1) + 12 = 8 ≠ 0.

x = 2

Q (2) = 2⁴ - 9 (2)² + 4 (2) + 12 = 0.

Dan sebagainya untuk setiap pembahagi. Dalam kes ini, faktor yang dijumpai adalah untuk x = -1 dan x = 2.

Kaedah Ruffini kini digunakan, mengikut mana pekali ekspresi akan dibahagikan dengan faktor -faktor yang dijumpai supaya pembahagian itu tepat. Istilah polinomial diperintahkan dari eksponen yang lebih besar ke bawah; Sekiranya istilah itu hilang dengan tahap yang berikut dalam urutan, 0 diletakkan di tempatnya.

Koefisien terletak dalam skim seperti yang dilihat dalam gambar berikut.

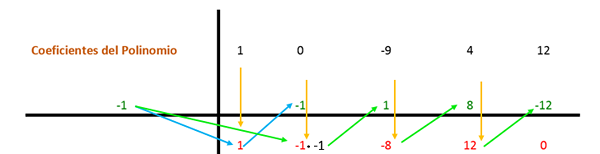
Pekali pertama diturunkan dan didarabkan oleh pembahagi. Dalam kes ini, pembahagi pertama adalah -1, dan hasilnya diletakkan dalam lajur berikut. Maka nilai pekali dengan hasil yang diperoleh ditambah secara menegak dan hasilnya diletakkan di bawah. Dengan cara itu proses diulang sehingga lajur terakhir.

Maka prosedur yang sama diulang lagi, tetapi dengan pembahagi kedua (iaitu 2) kerana ungkapan itu masih dapat dipermudahkan.

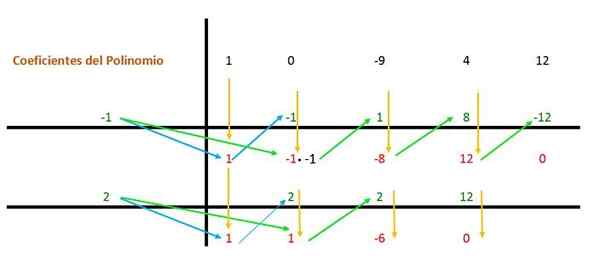
Oleh itu, bagi setiap akar yang dicapai polinomial akan mempunyai istilah (x - a), di mana "a" adalah nilai akar:

(x - (-1)) _* (x - 2) = (x + 1) _* (x - 2)

Sebaliknya, syarat -syarat ini harus didarabkan oleh selebihnya yang kekal dari peraturan Ruffini 1: 1 dan -6, yang merupakan faktor yang mewakili ijazah. Dengan cara ini, bentuk ungkapan adalah: (x² + X - 6).

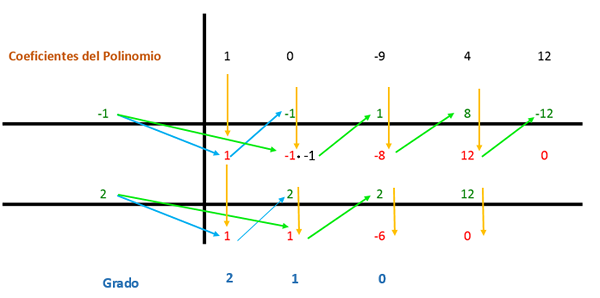
Mendapatkan hasil pemfaktoran polinomial oleh kaedah Ruffini adalah:

x⁴ - 9x² + 4x + 12 = (x + 1) _* (x - 2) _* (x² + X - 6)

Akhirnya, polinomial gred 2 yang muncul dalam ungkapan sebelumnya boleh ditulis semula sebagai (x+3) (x-2). Oleh itu, pemfaktoran akhir adalah:

x⁴ - 9x² + 4x + 12 = (x + 1) _* (x - 2)_*(x+3)_*(X-2).

Rujukan

1. Arthur Goodman, l. H. (Sembilan belas sembilan puluh enam). Algebra dan trigonometri dengan geometri analisis. Pendidikan Pearson.
2. J, v. (2014). Cara mengajar anak -anak mengenai pemfaktoran polinomial.
3. Manuel Morillo, a. S. (s.F.). Matematik asas dengan aplikasi.
4. Roelse, ms. L. (1997). Kaedah linear untuk pemfaktoran polinomial ke atas bidang terhingga: Teori dan pelaksanaan. Universiti Essen.
5. Sharpe, d. (1987). Cincin dan pemfaktoran.