Persamaan Kuadratik Umum, Contoh, Latihan

The Formula Umum, yang juga dikenali sebagai Formula pelarut Dalam sesetengah teks, ia digunakan untuk menyelesaikan persamaan darjah kedua: kapak² + bx + c = 0.

Di dalamnya ke, b dan c Mereka adalah nombor sebenar, dengan syarat bahawa ke berbeza dengan 0, makhluk x Tidak diketahui. Kemudian, formula umum membentangkan pelepasan yang tidak diketahui melalui ungkapan yang melibatkan nilai -nilai ke, b dan c seperti berikut:

Rajah 1. Formula umum dalam matematik digunakan untuk menyelesaikan persamaan kuadrat. Sumber: f. Zapata.

Dan melalui formula ini, anda dapat mencari penyelesaian mana -mana ijazah kedua atau persamaan kuadratik, dengan syarat penyelesaiannya ada.

Menurut ahli sejarah, formula umum sudah diketahui oleh matematik Babilon kuno. Ia kemudiannya dihantar kepada orang lain, seperti orang Mesir dan orang Yunani, melalui pertukaran budaya.

Formula dan variannya tiba di Eropah terima kasih kepada ahli matematik Muslim yang menetap di Semenanjung Iberia. Walau bagaimanapun, mereka tidak menggunakan notasi algebra yang kami gunakan sekarang. Notasi ini disebabkan oleh ahli matematik Perancis dan pakar kriptografi ke -16 Francois VIETE.

[TOC]

Persamaan Kuadratik oleh Formula Umum

Mari lihat bagaimana formula umum timbul, untuk mengesahkan kesahihannya. Bermula dari persamaan kuadrat umum:

kapak² + bx + c = 0

Mari kita mengamalkan beberapa manipulasi algebra yang mudah, untuk mencapai pelepasan yang tidak diketahui. Terdapat beberapa cara untuk membawa ini, contohnya menyelesaikan kotak, seperti yang ditunjukkan pada masa itu.

Demonstrasi formula umum

Kami mulakan dengan menambah (-c) di kedua-dua belah persamaan:

kapak² + Bx = - c

Dan sekarang ia didarab dengan 4A, selalu di kedua -dua belah persamaan, supaya tidak mengubah ungkapan:

Ke -4² x² + 4ab x = - 4ac

Menambah b²:

Ke -4²⋅x² + 4ab ⋅x + b² = - 4ac + b²

Tujuannya adalah untuk menyelesaikan dataran di sebelah kiri persamaan, yang mengandungi yang tidak diketahui, dengan cara ini pelepasannya difasilitasi. Oleh itu:

Boleh melayani anda: Pembahagi 8: Apa dan Penjelasan Mudah

-Istilah pertama: ke -4² x² Ia adalah persegi sempurna 2ax

-Yang terakhir, iaitu b², Ia adalah persegi sempurna b.

-Dan istilah pusat adalah produk berganda 2AX dan B: 2 ⋅2ax ⋅B = 4ABX

Oleh itu, kita mempunyai binomial persegi:

Ke -4²⋅x² + 4ab ⋅x + b² = (2ax + b)²

Dan kita boleh menulis:

(2ax + b)² = - 4ac + b²

Kami adalah satu langkah jauh dari membersihkan yang tidak diketahui x:

Dan kita sudah memperoleh formula umum yang kita tahu:

Ada cara lain untuk memanipulasi persamaan kuadratik secara algebra dan mendapatkan hasil yang sama.

Contoh penggunaan formula umum

Untuk memohon formula umum, nilai A, B dan C ditentukan dengan teliti dan digantikan dalam formula. Perhatikan simbol lebih kurang dalam pengangka; Ini menunjukkan bahawa kita mesti mempertimbangkan dua kemungkinan mengenai operasi, satu dengan tanda + dan satu dengan tanda -.

Persamaan kuadratik boleh mempunyai penyelesaian berikut, mengikut nilai kuantiti sub-radikal, yang dikenali sebagai membezakan:

-Ya b² - 4ac> 0, persamaan kuadratik mempunyai dua penyelesaian yang nyata dan berbeza.

-Apabila b² - 4ac = 0, persamaan mempunyai penyelesaian yang unik, yang diberikan oleh:

x = -b/2a

-Akhirnya, jika b² - 4ac < 0, la ecuación no tiene soluciones reales, pero sí tiene soluciones complejas.

Mari kita lihat beberapa contoh di mana formula umum digunakan, perhatikan bahawa jika mana -mana koefisien yang mengiringi yang tidak diketahui tidak muncul, difahami bahawa ia bernilai 1. Dan jika istilah bebas adalah yang tidak dijumpai, maka ia bernilai 0.

- Contoh 1

Selesaikan persamaan kuadrat berikut:

a) 6x² + 11x -10 = 0

b) 3x² -5x -1 = 0

Jawapan kepada

Kami menulis pekali setiap istilah: A = 6, b = 11, c = -10 dan menggantikan nilai dalam formula umum:

Boleh melayani anda: cukai

x = (-11 ± 19) /12

Hasilnya membawa kepada dua penyelesaian sebenar berikut:

x₁ = (-11 + 19)/12 = 8/12 = 2/3

x₂ = (-11 -19)/12 = -5/2

Jawab b

Sekali lagi pekali ditentukan: a = 3, b = -5 dan c = -1. Dengan menggantikan formula:

Tidak seperti kes sebelumnya, akar persegi 37 bukan integer, tetapi kita juga boleh meningkatkan kedua -dua penyelesaian dan meninggalkan akar atau mencari nilai perpuluhan yang sepadan dengan bantuan kalkulator:

x₁ = (-5 + √37)/6 ≈ 0.18

x₂ = (-5 - √37)/6 ≈ - 1.85

- Contoh 2

Selesaikan persamaan darjah kedua x² - 4x +13 = 0.

Jawapan

Seperti biasa, kami mengenal pasti nilai pekali dan menggantikan formula umum: a = 1, b = - 4, c = 13. Ini membawa kepada:

Kami mempunyai akar negatif, oleh itu penyelesaian persamaan ini adalah nombor kompleks. Akar boleh dinyatakan dari segi Yo, The Unit khayalan:

√ (36i²) = 6i

Sejak saya² = -1, oleh itu penyelesaian kompleks adalah:

x₁ = (4 + 6i)/2 = 2 + 3i

x₂ = (4 - 6i)/2 = 2 - 3i

Latihan diselesaikan

Tangga panjang 10 m terletak di dinding menegak, dengan kaki 6 m dari dinding itu. Tangga slip dan kaki dipisahkan 3 m lebih dari pangkalan.

Cari jarak menegak yang berjalan melalui bahagian atas tangga.

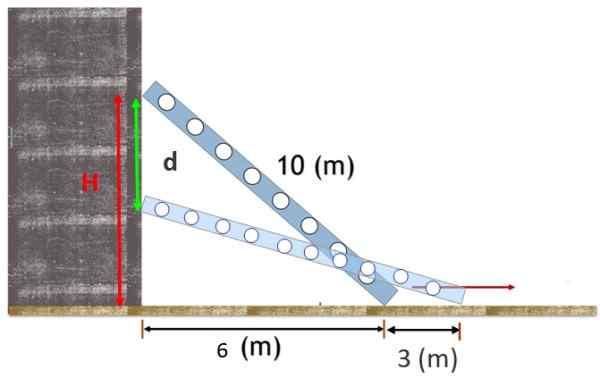Rajah 2. Tangga yang disokong pada dinding tergelincir sedikit dan berhenti atas bergerak secara menegak ke jarak d. Sumber: f. Zapata.

Penyelesaian

Untuk mencari jarak menegak yang meluncur bahagian atas tangga, anda perlu mencari kedudukan di mana ia pada asalnya mengenai tanah. Kita boleh melakukannya dengan teorem Pythagoras, kerana angka yang terbentuk adalah segitiga yang betul:

H = (10² - 6²) ^½ = 8 m

Setelah tangga tergelincir, jarak bergerak d, Ukur sejak bahagian atas adalah 8 m tinggi, sehingga mencapai kedudukan barunya, di (H-d) meter di atas tanah. Yang tidak diketahui adalah D.

Boleh melayani anda: kekerapan terkumpul: formula, pengiraan, pengedaran, contoh

Untuk menemuinya, kami mencadangkan segitiga segi empat tepat baru, yang terbentuk selepas tangga tergelincir sedikit. Segitiga ini masih mempunyai hypotenusa sama dengan 10 m dan Cateto selari kini 6m + 3m = 9 m, oleh itu:

(H-D)² = 10² - 9² = 100 - 81 = 19

Kami menggantikan H = 8m, sebelum ini dikira:

(8-d)² = 19

Persamaan dapat diselesaikan dalam beberapa cara, termasuk penggunaan formula umum, yang akan kita tunjukkan di bawah dengan langkah -langkah ini:

Langkah 1

Kembangkan kiri yang ketara di sebelah kiri:

64 -16D + D² = 19

Langkah 2

Mewujudkan persamaan ijazah kedua untuk tidak diketahui D:

d² - 16d + 45 = 0

Langkah 3

-Koefisien adalah: a = 1, b = -16 dan c = 45, kita menggantikannya dalam formula umum:

Penyelesaian persamaan adalah:

d₁ = (16 + √76)/2 ≈ 12.36 m

d₂ = (16 - √76)/2 ≈ 3.64 m

Langkah 4

Penyelesaian yang diperoleh dianalisis: Yang pertama tidak masuk akal fizikal, kerana tidak mungkin bagi tangga untuk menyusun 12.36 m, jika asalnya berhenti 8 m tinggi di tanah.

Oleh itu, jawapan yang betul adalah penyelesaian kedua: bahagian atas tangga slip d = 3.64 m.

Bolehkah pembaca menyelesaikan masalah dengan menggunakan kaedah lain?

Rujukan

1. Baldor. 1977. Algebra Elementary. Edisi Kebudayaan Venezuela.
2. Hoffman, J. Pemilihan masalah matematik. Jilid 2.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Stewart, J. 2006. Preccculment: Matematik untuk Pengiraan. 5th. Edisi. Pembelajaran Cengage.
5. Zill, d. 1984. Algebra dan trigonometri. McGraw Hill.