Mengakibatkan memaksa bagaimana latihan yang dikira dan diselesaikan

The kuasa Hasilnya Itu adalah jumlah semua kuasa yang bertindak pada badan yang sama. Apabila badan atau objek tertakluk kepada tindakan beberapa kuasa secara serentak berlaku. Kekuatan yang bertindak dapat digantikan oleh satu daya yang menghasilkan kesan yang sama. Kekuatan unik ini adalah daya yang dihasilkan juga dikenali sebagai daya bersih dan diwakili dengan simbol F_R .

Kesan yang dihasilkannya F_R Ia bergantung pada saiz, arah dan makna. Magnitud fizikal yang mempunyai arah dan makna adalah magnitud vektor.

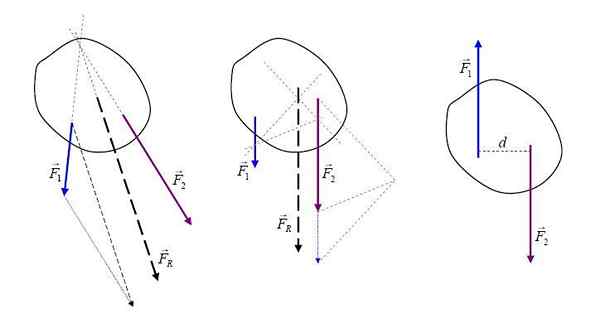Mengakibatkan kuasa. Oleh Ilevanat (https: // commons.Wikimedia.org/wiki/fail: rejultanta.JPG), dari Wikimedia Commons

Menjadi kekuatan yang bertindak pada magnitud badan dan vektor, daya yang dihasilkan F_R  Ia adalah jumlah vektor dari semua daya dan boleh diwakili secara grafik dengan anak panah yang menunjukkan arah dan makna.

Dengan daya yang terhasil, masalah badan yang terjejas oleh beberapa daya dipermudahkan dengan mengurangkannya kepada satu daya yang bertindak.

[TOC]

Formula

Perwakilan matematik daya yang dihasilkan adalah vektor musim panas kekuatan.

 F_R= ΣF          (1)

 ΣF = f₁+ F₂+ F₃+… F_N           (2)

F_R= Kekuatan yang dihasilkan

ΣF = Jumlah kuasa

N= Bilangan kuasa

Kekuatan yang dihasilkan juga boleh diwakili dengan persamaan undang -undang kedua Newton.

   F_R= m.ke          (3)

m= jisim badan

a = pecutan badan

Jika persamaan (1) digantikan dalam persamaan (3) persamaan berikut diperoleh:

ΣF = m.ke          (4)

F₁+ F₂+ F₃+… F_{N =} m.ke          (5)

Ekspresi Matematik (4) dan (5) memberikan maklumat mengenai status badan dengan mendapatkan pecutan vektor ke.

Bagaimana daya yang dihasilkan dikira?

Kekuatan yang dihasilkan diperoleh apabila memohon undang -undang kedua Newton yang menetapkan perkara berikut:

Boleh melayani anda: Jarak Jarak

Kekuatan bersih yang bertindak pada badan adalah sama dengan produk jisimnya dengan pecutan yang diperolehnya. (Persamaan (3))

Percepatan badan akan mempunyai arah daya bersih yang digunakan. Sekiranya semua daya yang bertindak di dalam badan diketahui, ia akan cukup untuk menambahkannya secara vektor untuk mendapatkan daya yang terhasil. Begitu juga, jika daya yang dihasilkan diketahui maka ia akan membahagikannya dengan badan badan untuk mendapatkan pecutannya.

Sekiranya daya yang terhasil tidak sah badan berehat atau kelajuan tetap. Sekiranya daya yang dihasilkan bertindak ke atas badan, daya tunggal adalah sama dengan daya itu F_R=F.

Apabila beberapa kuasa bertindak pada badan yang sama, komponen vektor daya mesti diambil kira, dan jika kuasa tersebut selari atau tidak.

Contohnya, jika kita secara mendatar meluncurkan buku yang diletakkan di atas meja. Daya dalam arah mendatar adalah satu -satunya yang memberikan pecutan kepada badan. Kekuatan bersih menegak pada buku itu sifar.

Sekiranya daya yang diterapkan pada buku mempunyai kecenderungan berkenaan dengan satah mendatar jadual, daya ditulis berdasarkan komponen menegak dan mendatar.

Hasilnya kuasa selari 

Kuasa selari yang bertindak pada badan adalah kekuatan yang bertindak ke arah yang sama. Mereka boleh mempunyai dua jenis rasa yang sama atau ke arah yang bertentangan.

Apabila daya yang bertindak pada badan mempunyai arah yang sama dan pengertian yang sama atau berada di arah yang bertentangan, daya yang dihasilkan diperolehi dengan melaksanakan jumlah algebra dari nilai berangka kekuatan.

Boleh melayani anda: aliran medan elektrik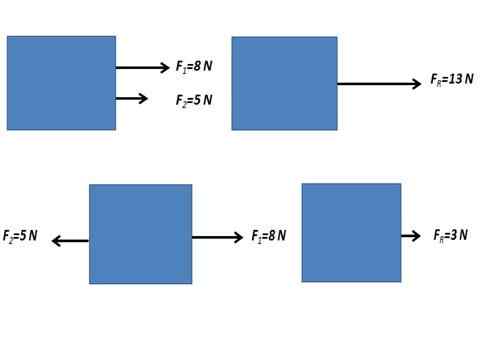Daya yang terhasil daripada dua daya selari.

Kuasa bukan -persamaan

Apabila daya bukan selalunya digunakan pada badan, daya yang terhasil akan mempunyai komponen segi empat tepat dan menegak. Ekspresi matematik untuk mengira daya bersih adalah:

F_R²= (Σ f_x)²+(Σ f_dan)²            (6)

Jadi θ_x= Σ f_dan / Σ f_x         (7)

Σ f_x  dan Σ f_x= Jumlah komponen algebra x dan dan kuasa yang digunakan

θ_x= sudut yang membentuk daya yang dihasilkan F_R Dengan paksi x

Perhatikan bahawa daya yang terhasil daripada ungkapan (6) tidak diserlahkan dalam huruf tebal dan ia hanya kerana ia hanya menyatakan nilai berangka. Alamat ditentukan oleh sudut θ_x.

Ungkapan (6) sah bagi kekuatan yang bertindak dalam satah yang sama. Apabila kuasa bertindak di angkasa, komponen diambil kira z kekuatan jika bekerja dengan komponen segi empat tepat.

Latihan yang diselesaikan

1. Tentukan daya yang terhasil daripada badan yang tertakluk kepada daya berikut yang ditunjukkan dalam imej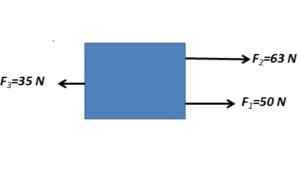

Daya selari ditambah dalam erti kata yang sama dan tolak dengan daya selari ke arah yang bertentangan

F_R= 63 n + 50 n - 35 n = 78n

Daya yang dihasilkan mempunyai magnitud 78n dengan arah mendatar.

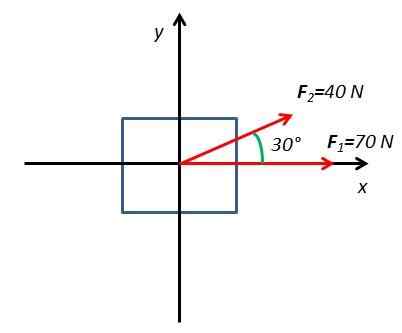
2.Kirakan daya yang terhasil daripada badan di bawah pengaruh dua daya F_{1 dan} F₂. Kekuatan F₁ Ia mempunyai magnitud 70n dan sedang digunakan secara mendatar. Kekuatan F₂ Ia mempunyai magnitud 40n dan sedang digunakan pada sudut 30 ° berkenaan dengan satah mendatar.

Untuk menyelesaikan latihan ini, gambarajah badan percuma dengan paksi koordinat ditarik x dan dan

Semua komponen ditentukan x dan dan kekuatan yang bertindak di badan. Kekuatan F₁ Ia hanya mempunyai komponen mendatar pada paksi x. Kekuatan F₂ Ia mempunyai dua komponen F_2x  dan f_{2 dan} yang diperoleh dari fungsi sinus dan kosinus sudut 30.

Boleh melayani anda: geseran: jenis, pekali, pengiraan, latihan

F_1x = F₁=70n

F_2x = F₂ Cos 30 ° = 40 n.Cos 30 ° = 34.64n

F_1y = 0

F_{2 dan}= F₂ tanpa 30 ° = 40 tanpa 30 ° = 20n

Σ f_x =70n+34.64n = 104.64n

Σ f_dan=20n+0 = 20n

Setelah daya yang dihasilkan pada paksi telah ditentukan x dan dan Nilai berangka daya yang dihasilkan diperolehi.

F_R²= (Σ f_x)²+(Σ f_dan)²

Daya yang dihasilkan adalah akar kuadrat dari jumlah musim panas komponen daya

F_R= √ (104.64n)²+(20n)²

F_R= 106,53n

Sudut yang membentuk daya yang terhasil F_R Ia diperoleh dari ungkapan berikut:

θ_x= tan^-1(Σ f_dan / Σ f_x)

θ_x= Jadi^-1(20n / 104,64n) = 10.82 °

Daya yang terhasil F_R Ia mempunyai magnitud 106.53n dan mempunyai arah yang ditentukan oleh sudut 10.82 ° yang terbentuk dengan mendatar.

Rujukan

1. Dola, G, Duffy, M dan Percival, ke. Fizik. Sepanyol: Heinemann, 2003.
2. Avison, J H. Dunia fizik. India: Thomas Nelson dan Anak -anak, 1989.
3. Pinsent, m. Proses fizikal. United Kingdom: Nelson Thomas, 2002.
4. Yadav, s k. Mekanik kejuruteraan. Delhi: Discovery Publishing House, 2006.
5. Serway, R A dan Jewett, J W. Fizik untuk saintis dan jurutera. California, Amerika Syarikat: Brooks/Cole, 2010.