Fungsi Bijektif Apa itu, Bagaimana Ia Dilakukan, Contoh, Latihan
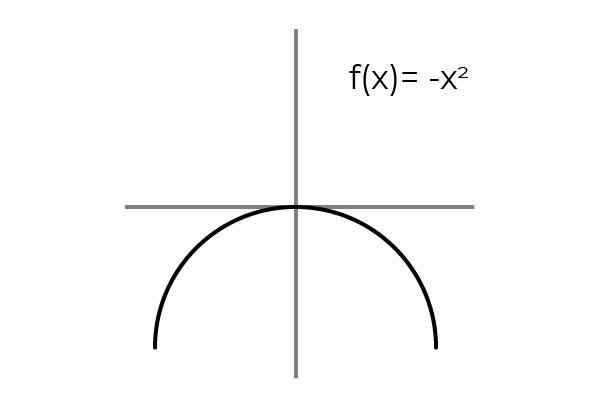
- 3112
- 719
- Dallas Bernhard
A Fungsi Bijektif Ia adalah salah satu yang memenuhi syarat berganda Injective dan overjective. Iaitu, semua elemen domain mempunyai imej tunggal dalam codominium, dan seterusnya codominium adalah sama dengan julat fungsi ( RF ).
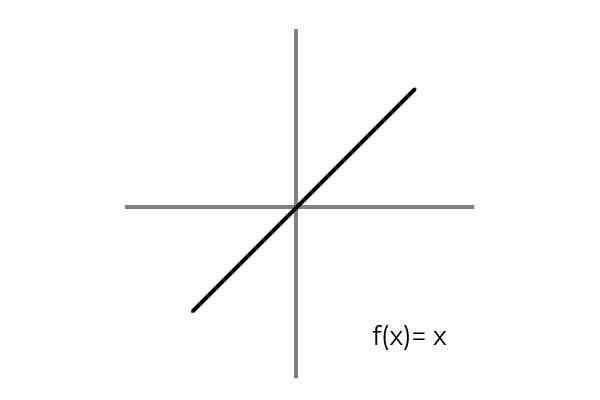
Ia dipenuhi apabila hubungan biunivocal antara unsur -unsur domain dan codominium dianggap. Contoh mudah ialah fungsi F: r → R ditakrifkan oleh garis F (x) = x
 Sumber: Pengarang
Sumber: Pengarang Diperhatikan bahawa bagi setiap nilai domain atau set berlepas (kedua -dua istilah digunakan secara sama) terdapat satu imej dalam codominium atau set ketibaan. Di samping itu tidak ada unsur codominium yang bukan gambar.
Oleh itu F: r → R ditakrifkan oleh garis F (x) = x adalah bijective
[TOC]
Bagaimana fungsi bijjective?
Untuk bertindak balas terhadap ini, perlu mempunyai konsep yang jelas berkaitan dengan Suntikan dan Kelebihan fungsi, Sebagai tambahan kepada kriteria untuk fungsi penyaman untuk menyesuaikannya dengan keperluan.
Suntikan fungsi
Fungsi adalah Injective Apabila setiap elemen domainnya berkaitan dengan satu elemen codominium. Unsur codominium hanya boleh menjadi imej satu elemen domain, dengan cara ini nilai pemboleh ubah bergantung tidak dapat diulang.
Untuk dipertimbangkan Injective Berikut ini mesti dipenuhi dengan fungsi:
∀ x1 ≠ x2 ⇒ f (x1 ) ≠ f (x2 )
Kelebihan fungsi
Fungsi dikelaskan sebagai Terlalu banyak, Sekiranya setiap elemen codominiumnya adalah imej sekurang -kurangnya satu elemen domain.
Untuk dipertimbangkan Terlalu banyak Berikut ini mesti dipenuhi dengan fungsi:
Boleh melayani anda: pensampelan penggantianMenjadi F: dF → CF
∀ b ℮ CF Dan ke ℮ DF / F (a) = b
Ini adalah cara algebra untuk menegaskan bahawa untuk setiap "b" yang dimiliki oleh cF Terdapat "A" yang dimiliki oleh DF sehingga fungsi yang dinilai dalam "A" adalah sama dengan "B".
Penyaman fungsi
Kadang -kadang fungsi yang tidak Bijektif, boleh menjalani penyesuaian tertentu. Keadaan baru ini dapat mengubahnya menjadi a Fungsi Bijektif. Semua jenis pengubahsuaian ke domain dan codominium fungsi adalah sah, di mana objektifnya adalah untuk memenuhi sifat suntikan dan lebih -lebih baik dalam hubungan yang sama.
Contoh: Latihan yang diselesaikan
Latihan 1
Menjadi fungsi F: r → R ditakrifkan oleh garis F (x) = 5x +1
A: [Semua nombor sebenar]
Diperhatikan bahawa untuk sebarang nilai domain terdapat imej dalam codominium. Imej ini unik, yang menjadikannya F jadi satu Fungsi Injektif. Dengan cara yang sama kita melihat bahawa codominium fungsi sama dengan julatnya. Dengan itu memenuhi syarat Kelebihan.
Menjadi injak dan berlebihan pada masa yang sama kita dapat menyimpulkan bahawa
F: r → R ditakrifkan oleh garis F (x) = 5x +1 ialah Fungsi Bijektif.
Ini terpakai kepada semua fungsi linear (fungsi yang tahap pembolehubah yang lebih besar adalah satu).
Latihan 2
Menjadi fungsi F: r → R ditakrifkan oleh F (x) = 3x2 - 2
Semasa melukis garis mendatar, diperhatikan bahawa grafik dijumpai pada lebih dari satu kali. Kerana ini fungsi F Ia bukan injak dan oleh itu tidak akan Bijektif Semasa ditakrifkan di R → R
Dengan cara yang sama terdapat nilai codominium yang bukan imej mana -mana elemen domain. Kerana ini fungsi itu tidak berlebihan, yang juga sesuai untuk keadaan ketibaan set.
Boleh melayani anda: Tetapkan Teori: Ciri, Elemen, Contoh, LatihanDomain dan codominium fungsi dikondisikan
F: [0 , ∞] → [ - 2 , ∞ ]
Di mana diperhatikan bahawa domain baru meliputi nilai dari sifar hingga infiniti positif. Mengelakkan pengulangan nilai yang mempengaruhi suntikan.
Oleh itu, codominium telah diubahsuai, mengira dari "-2" ke infiniti positif, menghapuskan dari codominium nilai-nilai yang tidak sesuai dengan mana-mana elemen domain
Dengan cara ini dapat dipastikan bahawa F : [0 , ∞] → [ - 2 , ∞ ] ditakrifkan oleh F (x) = 3x2 - 2
Ia adalah bijektif
Latihan 3
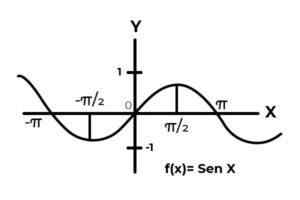
Menjadi fungsi F: r → r ditakrifkan oleh F (x) = dosa (x)
Dalam selang waktu [ -∞ , +∞ ] Fungsi sinus berbeza antara sifar dan satu.
 Sumber: Pengarang.
Sumber: Pengarang. Fungsinya F Ia tidak sesuai dengan kriteria suntikan dan kelebihan, kerana nilai pemboleh ubah bergantung diulang setiap selang π. Di samping itu syarat -syarat codominium di luar selang waktu [-Eleven] Mereka bukan imej unsur domain.
Semasa mengkaji grafik fungsi F (x) = dosa (x) selang diperhatikan di mana tingkah laku lengkung memenuhi kriteria BIJEKITI. Seperti selang waktu DF = [ π/2,3π/2 ] Untuk domain. Dan CF = [-1, 1] Untuk codominium.
Di mana fungsi berbeza dari 1 hingga -1, tanpa mengulangi sebarang nilai dalam pemboleh ubah bergantung. Dan pada masa yang sama Co -oominium sama dengan nilai yang diterima pakai oleh ungkapan Dosa (x)
Dengan cara ini fungsi F: [ π/2,3π/2 ] → [-1, 1] ditakrifkan oleh F (x) = dosa (x). Ia adalah bijektif
Latihan 4
Meningkatkan syarat yang diperlukan untuk dF dan cF. Jadi ungkapan
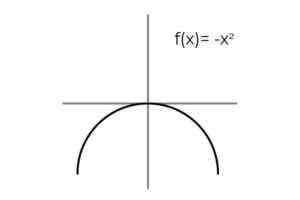
Boleh melayani anda: ralat pensampelan: formula dan persamaan, pengiraan, contohF (x) = -x2 Menjadi bijak.
 Sumber: Pengarang
Sumber: Pengarang Pengulangan hasil diperhatikan apabila pembolehubah mengambil nilai yang bertentangan:
F (2) = f (-2) = -4
F (3) = f (-3) = -9
F (4) = F (-4) = -16
Domain dikondisikan, mengehadkannya ke sebelah kanan garis sebenar.
DF = [0 , +∞ ]
Dengan cara yang sama diperhatikan bahawa julat fungsi ini adalah selang waktu [ -∞ , 0], yang, dengan berkhidmat sebagai codominium memenuhi syarat kelebihan.
Dengan cara ini kita dapat menyimpulkan bahawa
Ekspresi F: [0 , +∞ ] → [ -∞ , 0] ditakrifkan oleh F (x) = -x2 Ia adalah bijektif
Latihan yang dicadangkan
Sahkan jika fungsi berikut adalah bijective:
F: [0 , ∞) → R ditakrifkan oleh F (x) = 3 (x + 1)2 +2
F: [ 3π/2,5π/2 ] → R ditakrifkan oleh F (x) = 5ctg (x)
F: [ -π,π ] → R ditakrifkan oleh F (x) = cos (x - 3)
F: r → R ditakrifkan oleh garis F (x) = -5x + 4
Rujukan
- Pengenalan kepada logik dan pemikiran kritikal. Merrilee h. Salmon. Universiti Pittsburgh
- Masalah dalam analisis matematik. Piotr Bilar, Alfred Witkowski. Universiti Wroclaw. Tiang.
- Unsur analisis abstrak. Mícheál O'Searcoid PhD. Jabatan Matematik. Universiti Kolej Dublin, Beldfield, Dublind 4
- Pengenalan kepada Logik dan Metodologi Sains Deduktif. Alfred Tarski, New York Oxford. Oxford University Press.
- Prinsip Analisis Matematik. Enrique Linés Escardó. Editorial reverté s. Hingga 1991. Barcelona, Sepanyol.
- « Struktur glikogen, sintesis, degradasi, fungsi
- Ciri -ciri Enzim Ciri, Mekanisme Tindakan, Contoh »

