Fungsi, sifat, contoh yang berlebihan

A fungsi overjective Ini adalah hubungan di mana setiap elemen milik codominium adalah imej sekurang -kurangnya satu elemen domain. Juga dikenali sebagai fungsi mengenai, Mereka adalah sebahagian daripada klasifikasi fungsi mengenai cara di mana unsur -unsur mereka berkaitan.

Contohnya fungsi F: a → B ditakrifkan oleh F (x) = 2x

Yang dibaca "F yang pergi dari Ke sehingga B ditakrifkan oleh F (x) = 2x "

Sentuh menentukan set permulaan dan ketibaan A dan b.

A: 1, 2, 3, 4, 5 Sekarang nilai atau imej yang masing -masing elemen akan dikeluarkan apabila dinilai di F, Mereka akan menjadi unsur codominium.

F (1) = 2

F (2) = 4

F (3) = 6

F (4) = 8

F (5) = 10

Dengan itu membentuk set B: 2, 4, 6, 8, 10

Ia dapat disimpulkan kemudian:

F: 1, 2, 3, 4, 5  → 2, 4, 6, 8, 10 ditakrifkan oleh F (x) = 2x adalah fungsi yang berlebihan

Setiap elemen codominium mestilah sekurang -kurangnya satu operasi pemboleh ubah bebas melalui fungsi yang dipersoalkan. Tidak ada imej yang mengehadkan, elemen codominium boleh menjadi imej lebih dari satu elemen domain dan terus berurusan dengan a fungsi overjective.

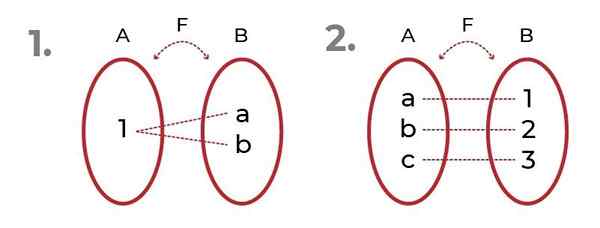
Imej menunjukkan 2 contoh dengan fungsi onjective.

Sumber: Pengarang

Pada yang pertama, diperhatikan bahawa imej boleh dirujuk ke elemen yang sama, tanpa menjejaskan Kelebihan fungsi.

Pada yang kedua kita melihat pengedaran yang saksama antara domain dan imej. Ini menimbulkan Fungsi Bijektif, di mana kriteria Fungsi injektif dan fungsi overjektif.

Kaedah lain untuk mengenal pasti fungsi onjective, adalah untuk mengesahkan jika codominium sama dengan pangkat fungsi. Ini bermaksud bahawa jika set ketibaan adalah sama dengan imej yang disediakan oleh fungsi semasa menilai pemboleh ubah bebas, Fungsinya terlalu banyak.

[TOC]

Sifat

Untuk dipertimbangkan Terlalu banyak Berikut ini mesti dipenuhi dengan fungsi:

Menjadi F: d_F → C_F

∀ b ℮ C_F  Dan ke ℮  D_F   / F (a) = b

Ini adalah cara algebra untuk menubuhkannya Untuk semua "B" yang dimiliki oleh C_F Terdapat "A" yang dimiliki oleh D_F  seperti itu, fungsi f yang dinilai dalam "A" adalah sama dengan "B". 

Ia dapat melayani anda: sifat radikal

Overbectivity adalah keanehan fungsi, di mana codominium dan pangkat adalah serupa. Oleh itu, unsur -unsur yang dinilai dalam fungsi membentuk set ketibaan.

Penyaman fungsi

Kadang -kadang fungsi yang tidak Terlalu banyak, boleh menjalani penyesuaian tertentu. Keadaan baru ini dapat mengubahnya menjadi a fungsi overjective.

Semua jenis pengubahsuaian ke domain dan codominium fungsi adalah sah, di mana objektifnya adalah untuk memenuhi sifat kelebihan dalam hubungan yang sepadan.

Contoh: Latihan yang diselesaikan

Untuk memenuhi syarat -syarat Kelebihan Teknik pengkondisian yang berbeza harus digunakan, ini untuk memastikan setiap elemen codominium berada dalam set imej fungsi.

Latihan 1

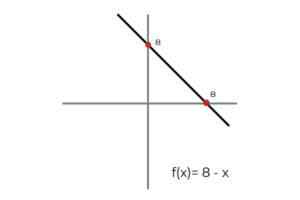
• Menjadi fungsi F: r → R ditakrifkan oleh garis F (x) = 8 - x

A: [Semua nombor sebenar]

Sumber: Pengarang

Dalam kes ini, fungsi ini menerangkan garis berterusan, yang merangkumi semua nombor sebenar dalam domain dan julat mereka. Kerana pangkat fungsi R_F Ia sama dengan codominium R Dapat disimpulkan bahawa:

F: r → R ditakrifkan oleh garis F (x) = 8 - x ialah fungsi overjective.

Ini terpakai kepada semua fungsi linear (fungsi yang tahap pembolehubah yang lebih besar adalah satu).

Latihan 2

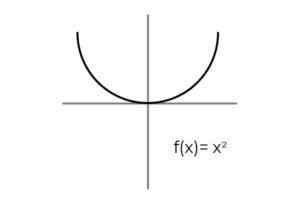
• Kaji fungsi F: r → R ditakrifkan oleh F (x) = x² : Tentukan jika ia adalah fungsi overjective. Sekiranya tidak, tunjukkan pengkondisian yang diperlukan untuk menjadikannya terlalu banyak.

Sumber: Pengarang

Perkara pertama yang perlu dipertimbangkan ialah codominium dari F, yang terdiri daripada nombor sebenar R. Tidak ada cara untuk fungsi membuang nilai negatif, yang tidak termasuk yang nyata di kalangan imej yang mungkin.

Penyejukan codominium selang [0 , ∞ ]. Dielakkan untuk meninggalkan unsur -unsur co -alomio tanpa berkaitan F.

Imej diulang untuk pasangan unsur pemboleh ubah bebas, seperti x = 1 dan x = - 1.  Tetapi ini hanya mempengaruhi Suntikan  fungsi, tidak menjadi masalah untuk kajian ini.

Boleh melayani anda: derivatif berturut -turut

Dengan cara ini dapat disimpulkan bahawa:

F: r  →[0, ∞ ) ditakrifkan oleh F (x) = x²    Ia adalah fungsi yang berlebihan

Latihan 3

• Tentukan syarat codominium yang mereka akan terlalu banyak untuk fungsi

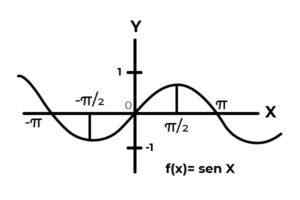
F: r  → R ditakrifkan oleh F (x) = dosa (x)

F: r  → R ditakrifkan oleh F (x) = cos (x)

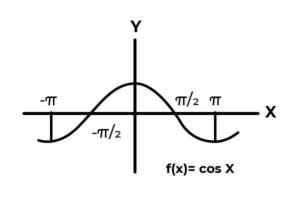Sumber: Pengarang Sumber: Pengarang.

Tingkah laku fungsi trigonometri serupa dengan gelombang, yang sangat biasa untuk mencari pengulangan pemboleh ubah bergantung antara imej. Juga dalam kebanyakan kes, julat fungsi adalah terhad kepada satu atau lebih sektor garis sebenar.

Ini adalah kes fungsi sinus dan kosinus. Di mana nilai mereka berubah-ubah dalam selang [-1, 1]. Selang masa mesti keadaan codominium untuk mencapai sampul fungsi.

F: r  →[-Eleven] ditakrifkan oleh F (x) = dosa (x)  Ia adalah fungsi yang berlebihan

F: r  →[-Eleven]ditakrifkan oleh F (x) = cos (x) Ia adalah fungsi yang berlebihan

Latihan 4

• Kaji fungsi

F: [0, ∞ ) → R ditakrifkan oleh F (x) = ± √x   menunjukkan jika ia adalah fungsi overjective

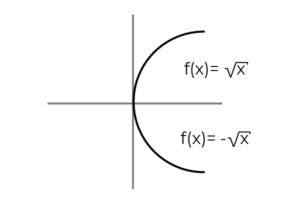Sumber: Pengarang

Fungsinya F (x) = ± √x  Ia mempunyai kekhususan yang mentakrifkan 2 pembolehubah bergantung pada setiap nilai "x" . Iaitu, julat menerima 2 elemen untuk setiap yang dijalankan di domain. Nilai positif dan negatif bagi setiap nilai "x" mesti disahkan untuk setiap nilai "x".

Apabila memerhatikan perhimpunan permulaan, diperhatikan bahawa domain telah dibatasi, ini untuk mengelakkan ketidakpatuhan yang dihasilkan ketika menilai nombor negatif dalam akar tork.

Apabila mengesahkan julat fungsi, ia menunjukkan bahawa setiap nilai codominium tergolong dalam julat.

Dengan cara ini dapat disimpulkan bahawa:

F: [0, ∞ ) → R ditakrifkan oleh F (x) = ± √x  Ia adalah fungsi yang berlebihan

Boleh melayani anda: vektor serentak: ciri, contoh dan latihan

Latihan 4

• Kaji fungsi F (x) = ln x  menunjukkan jika ia adalah fungsi overjective. Keadaan set ketibaan dan keberangkatan untuk menyesuaikan fungsi ke kriteria kelebihan.

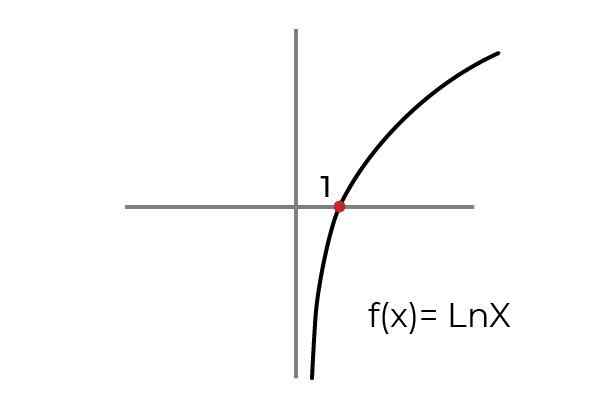Sumber: Pengarang

Seperti yang ditunjukkan dalam graf fungsi F (x) = ln xditakrifkan untuk nilai "x" lebih besar daripada sifar. Walaupun nilai "dan" atau imej dapat mengambil nilai sebenar.

Dengan cara ini kita dapat menyekat domain F (x) = hingga selang (0 , ∞ )

Walaupun pangkat fungsi dapat dikekalkan sebagai set nombor nyata R.

Memandangkan ini, dapat disimpulkan bahawa:

F: [0, ∞ ) → R ditakrifkan oleh F (x) = ln x  Ia adalah fungsi yang berlebihan

Latihan 5

• Kaji fungsi nilai mutlak F (x) = | X | dan menetapkan set ketibaan dan keberangkatan yang dikumpulkan untuk kriteria untuk Alegivity.

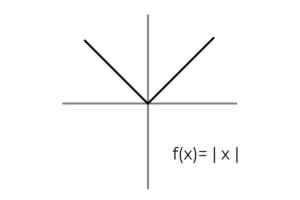Sumber: Pengarang

Domain fungsi dipenuhi untuk semua nombor sebenar R. Dengan cara ini satu -satunya penyaman mesti dijalankan dalam codominium, dengan mengambil kira bahawa fungsi nilai mutlak hanya memerlukan nilai positif.

Codominium fungsi ditubuhkan menyamakannya dengan julat yang sama

[0 , ∞ )

Sekarang dapat disimpulkan bahawa:

F: [0, ∞ ) → R ditakrifkan oleh F (x) = | X |  Ia adalah fungsi yang berlebihan

Latihan yang dicadangkan

1. Sahkan jika fungsi berikut terlalu banyak:

• F: (0, ∞ ) → R ditakrifkan oleh F (x) = log (x + 1)
• F: r → R ditakrifkan oleh F (x) = x³
• F: r →[1, ∞ )  ditakrifkan oleh F (x) = x²  + 1
• [0, ∞ ) → R ditakrifkan oleh F (x) = log (2x + 3)
• F: r → R ditakrifkan oleh F (x) = sec x
• F: r - 0 → R ditakrifkan oleh F (x) = 1 / x

Rujukan

1. Pengenalan kepada logik dan pemikiran kritikal. Merrilee h. Salmon. Universiti Pittsburgh
2. Masalah dalam analisis matematik. Piotr Bilar, Alfred Witkowski. Universiti Wroclaw. Tiang.
3. Unsur analisis abstrak. Mícheál O'Searcoid PhD. Jabatan Matematik. Universiti Kolej Dublin, Beldfield, Dublind 4
4.  Pengenalan kepada Logik dan Metodologi Sains Deduktif. Alfred Tarski, New York Oxford. Oxford University Press.
5.  Prinsip Analisis Matematik. Enrique Linés Escardó. Editorial reverté s. Hingga 1991. Barcelona, ​​Sepanyol.