Heptagon

Contoh Heptagon

Apa itu Heptagon?

Dia Heptagon Ia adalah poligon dengan tujuh sisi dan tujuh sudut dalaman. Sebagai perkataan geometri, perkataan heptagon berasal dari bahasa Yunani Hepta, yang bermaksud tujuh, dan Gonos, diterjemahkan sebagai sudut. Oleh itu, poligon dengan tujuh sudut.

Poligon adalah angka geometri rata yang membentuk dan menutup tiga atau lebih segmen, juga dipanggil sisi. Perkara umum yang dipanggil oleh pihak Simpang.

Rantau di antara sisi bersebelahan, di bahagian dalam angka, adalah Sudut dalaman, yang puncaknya juga merupakan salah satu simpang heptagon.

Sekiranya semua sisi dan sudut dalaman mempunyai ukuran yang sama, ia adalah Heptagon biasa, jika tidak, adalah Heptagon yang tidak teratur. Hepton yang tidak teratur mengamalkan pelbagai bentuk.

Heptagon juga boleh cembung Sama ada cekung, Mengikut ukuran sudut dalamannya. Sekiranya sudut dalaman mengukur kurang daripada 180 °, heptagon adalah cembung, tetapi jika satu atau lebih sudut tersebut melebihi 180 °, maka itu adalah cekung.

Heptagon yang sisinya adalah ukuran yang sama dipanggil Balat. Ini boleh dipercepat atau cembung, biasa atau tidak teratur.

Heptagon biasa dan tidak teratur

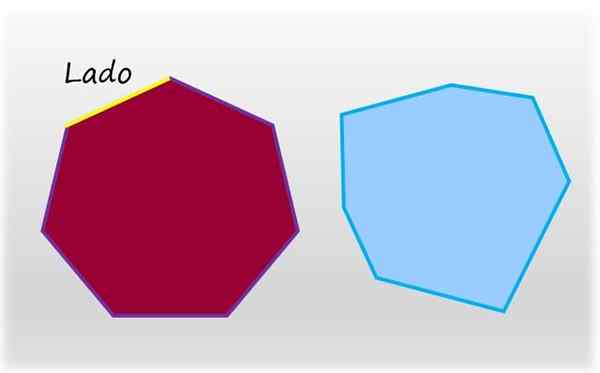Heptagon adalah angka rata dan tertutup tujuh sisi. Di sebelah kiri, heptagon biasa, yang sisi dan sudut dalamannya mempunyai ukuran yang sama. Di sebelah kanan, heptagon yang tidak teratur. Sumber: f. Zapata.

Heptagon biasa adalah salah satu yang mempunyai tujuh sisi dan tujuh sudut dalamannya yang sama, bertentangan dengan heptagon yang tidak teratur, yang mempunyai sekurang -kurangnya satu sisi ukuran yang berbeza, atau sudut dalaman yang berbeza.

Heptagon biasa

Simetri

Heptagon biasa adalah tokoh yang sangat simetri. Segmen boleh ditarik yang menghubungkan titik dengan titik tengah di seberang, semuanya bersilang di tengah -tengah heptagon. Ini adalah tujuh paksi simetri dalam angka.

Boleh melayani anda: kawasan pentagon biasa dan tidak teratur: bagaimana ia diambil, latihan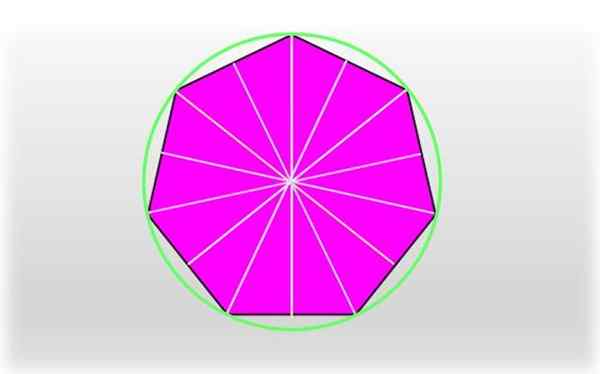 Heptagon biasa dan paksi simetrinya. Lilitan yang melewati setiap simpang heptagon dipanggil lilitan yang dilampirkan.

Segmen yang bergabung dengan puncak dengan pusat Heptagon dipanggil Circunradio, Ia sepadan dengan jejari lilitan unik yang melewati setiap simpang, seperti yang ditunjukkan dalam angka tersebut.

Sudut

Di Heptagon, sudut berikut menonjol:

• Sudut dalaman φ, yang puncaknya bertepatan dengan salah satu simpang heptagon, sebagai sisi sudut, dua sisi bersebelahan heptagon. Untuk heptagon biasa, ukuran setiap tujuh sudut dalaman adalah kira -kira 128.57 °.
• Sudut luaran, Yang membentuk antara salah satu sisi dan pemanjangan salah satu sisi bersebelahan, yang merupakan puncak umum di antara kedua -dua belah bahagian sudut sudut. Begitu juga, tujuh sudut luaran terbentuk dan nilai mereka dikira dengan menolak 180 ° dari sudut dalaman, yang untuk heptagon biasa, menghasilkan 51.43 °.
• Sudut pusat θ, Ia mempunyai puncaknya di tengah heptgon biasa. Ia dikira dengan membahagikan 360 ° oleh 7, yang mengakibatkan kira -kira 51.43 °.

Jumlah sudut dalaman dan sudut pusat adalah sama dengan 180 °, iaitu:

φ + θ = π

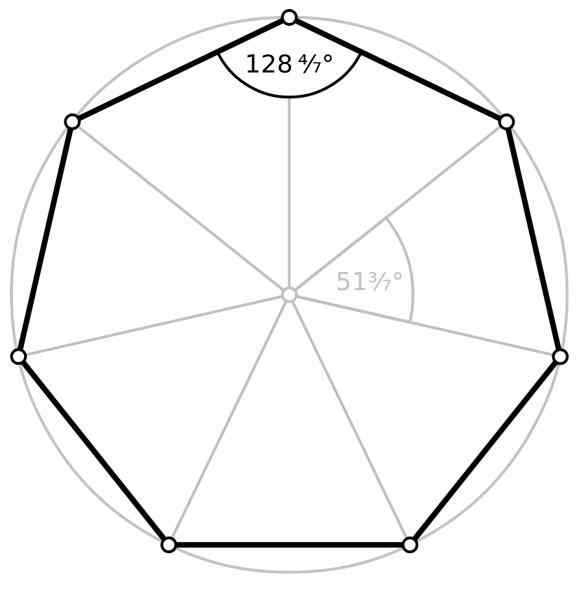Sudut dalaman dan sudut pusat heptagon biasa. Sumber: Wikimedia Commons

Kawasan

Bagi Heptagon biasa terdapat formula, sementara untuk heptagon yang tidak teratur, anda harus menggunakan kaedah lain, seperti membahagikannya ke poligon lain yang lebih mudah, seperti segitiga.

Ia boleh melayani anda: Peraturan T: Ciri -ciri, supaya ia, contohnya

Kawasan Heptagon biasa

1. Sekiranya perimeter p dan apotheme ke_p:

Sama ada di kawasan Heptagon. Terdapat formula untuk mengira kawasan tersebut, sah untuk mana -mana poligon biasa:

2. Sekiranya L dan Apothem diketahui ke_p:

Oleh kerana perimeter adalah jumlah sisi, dan langkah -langkah sampingan l dalam heptagon biasa, ia diperolehi:

P = 7 ⋅ l

Menggantikan formula sebelumnya:

3. Sekiranya bahagian itu dikenali        

Berikut adalah formula anggaran, yang sah apabila ukuran heptagon diketahui:

A = 3.634 ∙ l²

Kawasan Heptagon yang tidak teratur

Kawasan heptagon yang tidak teratur dapat dikira oleh Triangulasi, yang terdiri daripada membahagikan heptagon menjadi lima segitiga (lihat angka berikut). Kawasan masing -masing dikira dan hasilnya ditambah, dengan itu memperoleh kawasan lengkap heptagon.

Kaedah lain dipanggil Penentu Gauss, Dan perlu meletakkan heptagon dalam sistem koordinat segi empat tepat, untuk mengetahui koordinat setiap puncak. Kawasan ini dikira oleh formula yang melibatkan nilai koordinat ini.

Diagonal

The Diagonal Mereka adalah segmen yang menghubungkan puncak dengan yang lain yang tidak berturut -turut (jika segmen menghubungkan dua simpang berturut -turut adalah sisi). Heptagon mempunyai 14 pepenjuru.

Bilangan pepenjuru d dari mana -mana poligon, dikira melalui formula:

D = n · (n - 3) / 2

Menggantikan n = 7, kekal:

D = 7 · (7 - 3) / 2 = 7 · (4/2) = 14

Jumlah sudut dalaman

Bagi mana -mana heptagon, tanpa mengira sama ada ia biasa atau tidak, jumlah sudut dalamannya sama dengan 900 ° atau 5 π radians.

Ia boleh melayani anda: Sebab Trigonometrik: Contoh, Latihan dan Aplikasi

Harta ini sangat mudah untuk ditunjukkan, kerana ini heptagon dibahagikan kepada segitiga individu yang tidak bertindih, melukis segmen rectilinear yang menyatukan simpul, tanpa melintasi satu sama lain.

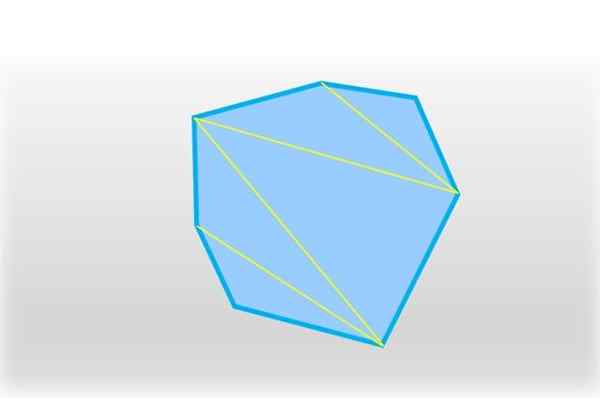Heptagon boleh dibahagikan kepada lima segitiga, bergabung dengan segmen dua simpang bukan. Sumber: f. Zapata.

Lima segitiga diperoleh dan dalam setiap satu, jumlah sudut dalamannya adalah 180 °, yang didarab dengan 5 adalah sama dengan 900 °:

5 x 180 ° = 900 °

Formula

Perimeter

Untuk heptagon biasa dari L, perimeter p dikira seperti berikut:

P = 7 ⋅ l

Sekiranya perimeter tidak teratur, panjang setiap tujuh sisi ditambah.

Ukuran sudut dalaman

Dalam heptagon biasa, sudut dalaman θ mengukur:

θ = [180 (n-2)]/n

Di mana n = 7.

Apothem

Jadilah sisi heptagon biasa. Apothem adalah segmen yang keluar dari pusat heptagon, tegak lurus ke seberang.

Biarkan a_p Panjang apotheme. Mengetahui jejari lilitan yang dilampirkan, yang dilambangkan sebagai r r_c Dan sisi L Heptagon, anda mempunyai:

Mengetahui sudut dalaman θ, di atas bersamaan dengan:

Kawasan

Jika ia adalah heptagon biasa dari L, kawasan A diberikan oleh:

A = 3.634 ∙ l²

Apabila heptagon tidak teratur, koordinat segi empat tepat setiap puncak diperlukan, diberikan oleh (x_n , dan_n), Di mana n = 1, 2, 3 ... 7.

Kemudian formula berikut digunakan untuk mencari Kawasan A:

Diagonal

Bilangan D dari pepenjuru diberikan oleh:

D = n · (n - 3) / 2

Di mana n = 7 untuk heptagon.

Cara Membuat Heptagon

Animasi berikut menunjukkan cara menarik kira -kira heptagon biasa, menggunakan peraturan dan kompas.

Pembinaan heptagon biasa. Sumber: Wikimedia Commons

Rujukan

1. Alexander, d. 2013. Geometri. 5th. Edisi. Pembelajaran Cengage.
2. Lemonis, m. Kalkulator Hepalle biasa. Pulih dari: calcresource.com.
3. Rujukan terbuka matematik. Kawasan Poligon. Pulih dari: Mathpenref.com.
4. Formula Universe. Heptagon. Pulih dari: universoformulas.com.
5. Wikipedia. Heptagon. Pulih dari: Adakah.Wikipedia.com.