Homocedicity apa, kepentingan dan contoh

The Homocedicity Dalam model statistik ramalan, ia berlaku jika dalam semua kumpulan data satu atau lebih pemerhatian, varians model berkenaan dengan pembolehubah penjelasan (atau bebas).

Model regresi boleh homocedastic atau tidak, dalam hal ini kita bercakap Heterocedicity.

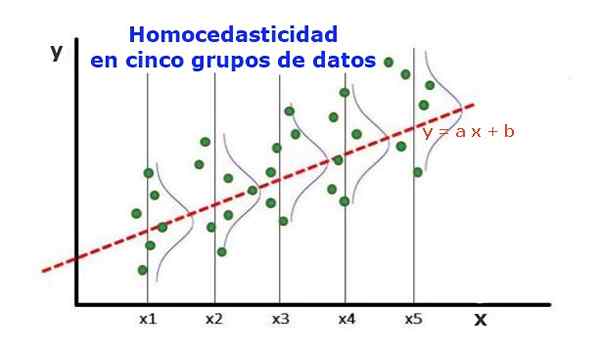
Rajah 1. Lima kumpulan data dan pelarasan regresi set. Varians mengenai nilai yang diramalkan adalah sama dalam setiap kumpulan. (Upav-library.org)

Model regresi statistik beberapa pembolehubah bebas dipanggil homocedastic, hanya jika varians ralat pembolehubah yang diramalkan (atau sisihan piawai pembolehubah bergantung) kekal seragam untuk kumpulan yang berlainan dari pembolehubah penjelasan atau bebas.

Dalam lima kumpulan data dalam Rajah 1, varians telah dikira dalam setiap kumpulan, berkenaan dengan nilai yang dianggarkan oleh regresi, berubah menjadi sama dalam setiap kumpulan. Juga diandaikan bahawa data mengikuti taburan normal.

Pada tahap grafik ini bermakna titik -titik yang sama tersebar atau bertaburan di sekitar nilai yang diramalkan oleh pelarasan regresi, dan model regresi mempunyai ralat dan kesahihan yang sama untuk julat pemboleh ubah penjelasan.

[TOC]

Kepentingan homocedicity

Untuk menggambarkan kepentingan homocedasticity dalam statistik ramalan, perlu dibezakan dengan fenomena yang bertentangan, heterocedicity.

Homocedasticity versus heterocedicity

Dalam kes Rajah 1, di mana terdapat homocedicity, ia dipenuhi bahawa:

Var ((y1-y1); x1) ≈ var ((y2-y2); x2) ≈ ... var (y4-y4); x4)

Di mana var ((yi-ii); xi) mewakili varians, pasangan (xi, yi) mewakili fakta kumpulan I, manakala yi adalah nilai yang meramalkan regresi bagi nilai xi purata kumpulan. Varians data kumpulan I dikira seperti berikut:

Var ((yi -ii); xi) = Σj (yij - yi)^2/n

Sebaliknya, apabila heterocedicity berlaku, model regresi mungkin tidak sah untuk seluruh rantau di mana ia dikira. Rajah 2 menunjukkan contoh keadaan ini.

Boleh melayani anda: Apakah sudut alternatif dalaman? (Dengan latihan)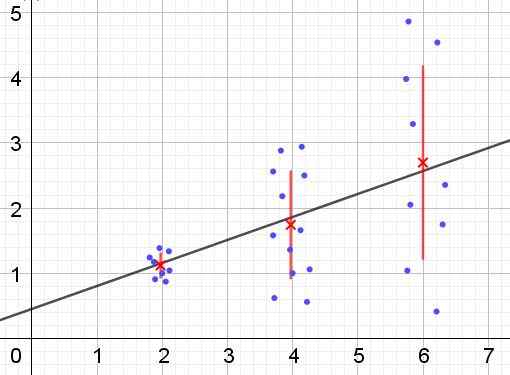 Rajah 2. Kumpulan data yang mempunyai heterocedicity. (Huraian sendiri)

Dalam Rajah 2 tiga kumpulan data dan set set diwakili oleh regresi linear. Harus diingat bahawa data di kedua dan dalam kumpulan ketiga lebih bertaburan daripada kumpulan pertama. Grafik Rajah 2 juga menunjukkan nilai purata setiap kumpulan dan bar ralatnya ± σ, sebagai sisihan piawai σ bagi setiap kumpulan data. Harus diingat bahawa sisihan piawai σ adalah akar kuadrat dari varians.

Sudah jelas bahawa dalam hal heterocedicity, kesilapan anggaran regresi berubah dalam julat nilai pemboleh ubah penjelasan atau bebas, dan dalam selang waktu kesilapan ini sangat besar, ramalan oleh regresi tidak dapat dipercayai atau tidak berkaitan.

Dalam model regresi, kesilapan atau sisa (y -y) mesti diedarkan dengan varians yang sama (σ^2) sepanjang selang nilai pembolehubah bebas. Oleh sebab itu, model regresi yang baik (linear atau bukan linear) mesti lulus ujian homocedasticity. 

Ujian Homocedicity

Titik yang ditunjukkan dalam Rajah 3 sesuai dengan data kajian yang mencari hubungan antara harga (dalam dolar) rumah bergantung pada saiz atau kawasan dalam meter persegi.

Model pertama yang dibacakan ialah regresi linear. Pada mulanya diperhatikan bahawa pekali penentuan r^2 pelarasan agak tinggi (91%), jadi dapat dianggap bahawa pelarasan itu memuaskan.

Walau bagaimanapun, dua wilayah dapat dibezakan dengan jelas dari graf pelarasan. Salah satu daripada mereka, yang di sebelah kanan terkunci di bujur, memenuhi homocedasticity, sementara rantau kiri tidak mempunyai homocedasticity.

Boleh melayani anda: gred polinomial: bagaimana ia ditentukan, contoh dan latihan

Ini bermakna bahawa ramalan model regresi adalah mencukupi dan boleh dipercayai dalam julat antara 1800 m^2 hingga 4800 m^2 tetapi sangat tidak mencukupi di luar rantau ini. Di kawasan heterocedic bukan sahaja kesilapannya sangat besar, tetapi juga data seolah -olah mengikuti trend lain yang berbeza dari yang dicadangkan oleh model regresi linear.

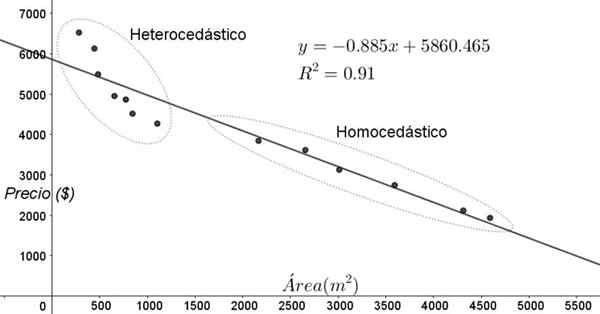Rajah 3. Harga perumahan vs kawasan dan model ramalan oleh regresi linear, menunjukkan homocedasticity dan kawasan heterocedicity. (Huraian sendiri)

Grafik penyebaran data adalah ujian paling mudah dan paling visual mengenai homocedasticity mereka, namun kadang -kadang ia tidak begitu jelas seperti dalam contoh yang ditunjukkan dalam Rajah 3, adalah perlu untuk menggunakan grafik dengan pembolehubah tambahan.

Pembolehubah standard

Dengan tujuan memisahkan kawasan di mana homocedasticity dipenuhi dan di mana tidak, pembolehubah standard ZREs dan zreded diperkenalkan:

Zres = abs (y - y)/σ

Zpred = y/σ

Harus diingat bahawa pembolehubah ini bergantung kepada model regresi yang digunakan, kerana ia adalah nilai ramalan regresi. Berikut adalah graf penyebaran ZRES vs ZRED untuk contoh yang sama:

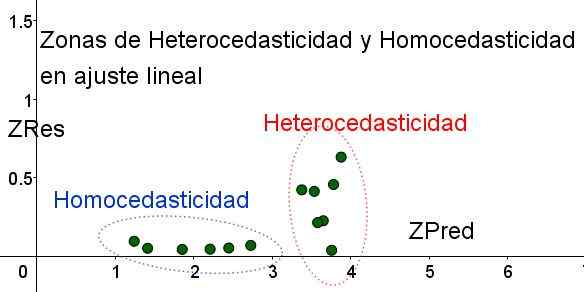Rajah 4. Harus diingat bahawa di zres zon homocedasticity kekal seragam dan kecil di rantau ramalan (penghuraian sendiri).

Dalam graf Rajah 4 dengan pembolehubah piawai, kawasan di mana ralat sisa kecil dan seragam jelas dipisahkan, berkenaan dengan yang tidak. Di kawasan pertama, homocedasticity dipenuhi sementara ralat sisa sangat berubah dan besar.

Pelarasan regresi digunakan untuk kumpulan data yang sama 3. Hasilnya ditunjukkan dalam angka berikut:

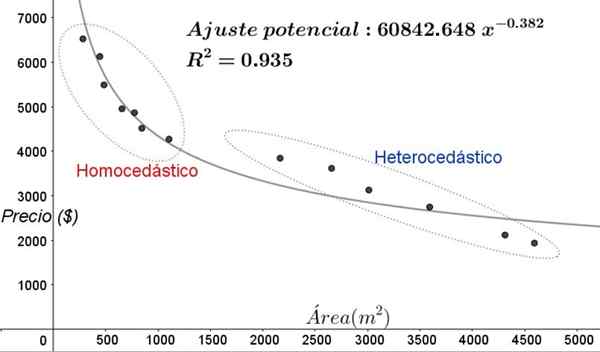Rajah 5. Homocedasticity dan kawasan heterocedicity baru dalam pelarasan data dengan model regresi bukan lineal. (Huraian sendiri).

Dalam graf Rajah 5, kawasan homokedik dan heterocedicastic harus diperhatikan dengan jelas. Perlu juga diperhatikan bahawa kawasan -kawasan ini ditukar berkenaan dengan yang terbentuk dalam model pelarasan linear.

Boleh melayani anda: jenis sudut, ciri dan contoh

Dalam graf Rajah 5, jelas bahawa walaupun terdapat pekali penentuan pelarasan yang agak tinggi (93.5%), model ini tidak sesuai untuk keseluruhan selang pemboleh ubah penjelasan, kerana data untuk nilai yang lebih tua dari 2000 M^2 mempunyai heterocedasticity.

Ujian homocedasticity non -lographic

Salah satu ujian nonografik yang paling banyak digunakan untuk mengesahkan sama ada homocedasticity dipenuhi atau tidak adalah Ujian Breusch-Pagan.

Semua butiran ujian ini tidak akan diberikan dalam artikel ini tetapi ciri -ciri asasnya dan langkah -langkah yang sama digariskan secara meluas:

1. Model regresi digunakan untuk data N dan varians yang sama dikira berkenaan dengan nilai yang dianggarkan oleh model σ^2 = Σj (yj - y)^2/n.
2. Pembolehubah baru ε = ((yj - y)^2) / (σ^2) ditakrifkan
3. Model regresi yang sama digunakan untuk pemboleh ubah baru dan parameter regresi baru dikira.
4. Nilai kritikal Chi Square (χ^2) ditentukan, ini menjadi separuh daripada jumlah kuadrat sisa baru dalam pembolehubah ε.
5. Jadual pengedaran Chi Square digunakan memandangkan tahap kepentingan pada paksi x (biasanya 5%) dan bilangan darjah kebebasan (pembolehubah regresi #of kecuali unit), untuk mendapatkan nilai lembaga.
6. Nilai kritikal yang diperolehi dalam langkah 3 dibandingkan dengan nilai yang terdapat dalam jadual (χ^2).
7. Sekiranya nilai kritikal berada di bawah jadual anda mempunyai hipotesis nol: ada homocedicity
8. Sekiranya nilai kritikal berada di atas meja, anda mempunyai hipotesis alternatif: tidak ada homocedasticity.

Kebanyakan pakej komputer statistik seperti: SPSS, Minitab, R, Python Pandas, SAS, Statgraphic dan beberapa yang lain menggabungkan ujian homocedasticity Breusch-Pagan. Ujian lain untuk mengesahkan keseragaman varians Ujian Levene.

Rujukan

1. Kotak, Hunter & Hunter. (1988) Statistik untuk penyelidik. Saya membalikkan editor.
2. Johnston, J (1989). Kaedah Econometrics, Vicens -Ives Editores.
3. Murillo dan González (2000). Manual Econometry. Universiti Las Palmas De Gran Canaria. Diperolehi dari: ULPGC.adalah.
4. Wikipedia. Homocedicity. Pulih dari: Adakah.Wikipedia.com
5. Wikipedia. Homoscedasticity. Diperoleh dari: dalam.Wikipedia.com