Peraturan empirikal bagaimana untuk menerapkannya, apa itu, latihan diselesaikan

A Peraturan empirikal Ini adalah hasil pengalaman praktikal dan pemerhatian kehidupan sebenar. Sebagai contoh, anda dapat mengetahui bahawa spesies burung dapat diperhatikan di tempat -tempat tertentu pada setiap masa tahun dan pemerhatian itu dapat ditubuhkan "peraturan" yang menggambarkan kitaran hidup burung -burung ini.

Dalam statistik, peraturan empirikal merujuk kepada bentuk pengumpulan pemerhatian di sekitar nilai pusat, purata atau purata, dalam unit sisihan piawai.

Katakan anda mempunyai sekumpulan orang dengan ketinggian purata 1.62 meter dan sisihan piawai 0.25 meter, maka peraturan empirikal akan membolehkan untuk menentukan, contohnya, berapa banyak orang yang akan berada dalam selang rata -rata lebih kurang sisihan piawai?

Menurut peraturan, 68% daripada data lebih kurang sisihan piawai purata, iaitu, 68% orang kumpulan akan mempunyai ketinggian antara 1.37 (1.62-0.25) dan 1.87 (1.62+0.25) meter.

[TOC]

Dari mana peraturan empirikal berasal?

Peraturan empirikal adalah penyebaran teorem Tchebyshev dan pengedaran normal.

THE THEOREM TCHebyshev

Teorem Tchebyshev mengatakan bahawa: untuk beberapa nilai k> 1, kebarangkalian bahawa pemboleh ubah rawak adalah antara purata kurang k kali sisihan piawai, dan purata kali lebih, sisihan piawai lebih besar daripada atau sama dengan (1 -1 /k²).

Kelebihan teorem ini adalah bahawa ia terpakai kepada pembolehubah rawak diskret atau berterusan dengan sebarang taburan kebarangkalian, tetapi peraturan yang ditakrifkan daripadanya tidak selalu sangat tepat, kerana ia bergantung pada simetri pengedaran. Lebih tidak simetri Pengagihan pemboleh ubah rawak, kurang diselaraskan dengan peraturan akan menjadi kelakuannya.

Peraturan empirikal yang ditakrifkan dari teorem ini adalah:

Jika k = √2, dikatakan bahawa 50% daripada data berada dalam selang: [μ - √2 s, μ + √2 s]

Jika k = 2, dikatakan bahawa 75% daripada data berada dalam selang: [μ - 2 s, μ + 2 s]

Jika k = 3, dikatakan bahawa 89% daripada data berada dalam selang: [μ - 3 s, μ + 3 s]

Taburan normal

Pengagihan normal, atau loceng Gauss, membolehkan untuk menetapkan peraturan empirikal atau Peraturan 68 - 95 - 99.7.

Boleh melayani anda: perkadaran

Peraturan ini berdasarkan kebarangkalian berlakunya pemboleh ubah rawak pada selang antara purata kurang satu, dua atau tiga penyimpangan piawai dan purata ditambah satu, dua atau tiga sisihan piawai.

Peraturan empirikal mentakrifkan selang berikut:

68.27% daripada data berada dalam selang: [μ - s, μ + s]

95.45% daripada data berada dalam selang: [μ - 2s, μ + 2s]

99.73% daripada data berada dalam selang: [μ - 3s, μ + 3s]

Dalam angka, anda dapat melihat bagaimana selang -selang ini dibentangkan dan hubungan di antara mereka dengan meningkatkan lebar asas grafik.

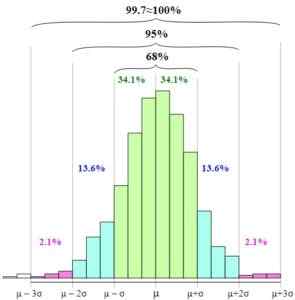Peraturan empirikal. Melikamp [CC BY-SA 4.0 (https: // creativeCommons.org/)] penyeragaman pemboleh ubah rawak, iaitu, ungkapan pemboleh ubah rawak dari segi pemboleh ubah standard atau normal, memudahkan penggunaan peraturan empirikal, kerana pembolehubah z mempunyai purata sama dengan sifar dan sisihan piawai sama kepada satu.

Oleh itu, penerapan peraturan empirikal pada skala pembolehubah normal standard, z, mentakrifkan selang berikut:

68.27% daripada data berada dalam selang: [-1, 1]

95.45% daripada data berada dalam selang: [-2, 2]

99.73% daripada data berada dalam selang: [-3, 3]

Cara menerapkan peraturan empirikal?

Peraturan empirikal membolehkan anda menyingkat pengiraan semasa bekerja dengan taburan normal.

Katakan bahawa sekumpulan 100 pelajar universiti mempunyai umur purata 23 tahun, dengan sisihan piawai 2 tahun. Maklumat apa yang dibenarkan oleh peraturan empirikal?

Permohonan peraturan empirikal menyiratkan mengikuti langkah -langkah:

1- Bina selang peraturan

Oleh kerana purata adalah 23 dan sisihan piawai adalah 2, maka selang waktu adalah:

[μ - s, μ + s] = [23 - 2, 23 + 2] = [21, 25]

[μ - 2s, μ + 2s] = [23 - 2 (2), 23 + 2 (2)] = [19, 27]

[μ - 3s, μ + 3s] = [23 - 3 (2), 23 + 3 (2)] = [17, 29]

2- Kirakan bilangan pelajar dalam setiap selang mengikut peratusan

(100)*68.27% = 68 pelajar lebih kurang

(100)*95.45% = Kira -kira 95 pelajar

(100)*99.73% = 100 pelajar

3- Selang umur dikaitkan dengan jumlah pelajar dan ditafsirkan

Sekurang -kurangnya 68 pelajar berusia antara 21 hingga 25 tahun.

Boleh melayani anda: Statistik deskriptif: sejarah, ciri, contoh, konsep

Sekurang -kurangnya 95 pelajar berusia antara 19 dan 27 tahun.

Hampir 100 pelajar berusia antara 17 hingga 29 tahun.

Apakah peraturan empirikal untuk?

Peraturan empirikal adalah cara yang cepat dan praktikal untuk menganalisis data statistik, semakin dipercayai sehingga sejauh mana pengedarannya dekat dengan simetri.

Kegunaannya bergantung pada medan di mana ia digunakan dan soalan yang timbul. Sangat berguna untuk mengetahui bahawa berlakunya nilai tiga sisihan piawai hampir tidak mungkin di bawah atau lebih purata, walaupun untuk pembolehubah pengedaran bukan normal, sekurang -kurangnya 88.8% kes berada dalam selang tiga sigma.

Dalam sains sosial, hasil yang umumnya konklusif adalah selang purata lebih kurang dua sigma (95%), manakala dalam fizik zarah, kesan baru memerlukan selang lima sigmas (99.99994%) dianggap sebagai penemuan.

Latihan yang diselesaikan

Arnab di simpanan

Dalam rizab hidupan liar dianggarkan bahawa terdapat purata 16.000 arnab dengan sisihan piawai 500 arnab. Sekiranya pengedaran 'bilangan arnab dalam rizab' pembolehubah tidak diketahui, adakah mungkin.000 dan 17.000 arnab?

Selang boleh dibentangkan dalam istilah ini:

15000 = 16000 - 1000 = 16000 - 2 (500) = μ - 2 s

17000 = 16000 + 1000 = 16000 + 2 (500) = μ + 2 s

Oleh itu: [15000, 17000] = [μ - 2 s, μ + 2 s]

Memohon teorem Tchebyshev, terdapat kebarangkalian sekurang -kurangnya 0.75 bahawa penduduk arnab rizab hidupan liar adalah antara 15.000 dan 17.000 arnab.

Rata -rata kanak -kanak dari negara

Berat purata satu kanak -kanak -kanak -kanak yang biasa diedarkan dengan purata 10 kilogram dan sisihan piawai kira -kira 1 kilogram.

a) Anggarkan peratusan satu kanak -kanak di negara ini yang mempunyai berat purata antara 8 dan 12 kilogram.

8 = 10 - 2 = 10 - 2 (1) = μ - 2 s

12 = 10 + 2 = 10 + 2 (1) = μ + 2 s

Oleh itu: [8, 12] = [μ - 2s, μ + 2s]

Ia boleh melayani anda: Ujian Tukey: Apa, dalam hal contoh, diselesaikan senaman

Menurut peraturan empirikal, dapat ditegaskan bahawa 68.27% kanak -kanak di negara ini mempunyai berat antara 8 dan 12 kilogram.

b) Berapakah kebarangkalian mencari anak satu tahun yang berjumlah 7 kilogram atau kurang berat?

7 = 10 - 3 = 10 - 3 (1) = μ - 3 s

Diketahui bahawa berat 7 kilogram mewakili nilai μ - 3s, dan juga diketahui bahawa 99.73% kanak -kanak antara 7 dan 13 kilogram berat. Yang meninggalkan hanya 0.27% daripada jumlah kanak -kanak untuk melampau. Separuh daripada mereka, 0.135%, mempunyai 7 kilogram berat atau kurang dan separuh lagi, 0.135%, mempunyai 11 kilogram berat atau lebih.

Jadi, dapat disimpulkan bahawa terdapat kebarangkalian 0.00135 bahawa kanak -kanak mempunyai berat 7 kilogram atau kurang.

c) Sekiranya penduduk di negara ini mencapai 50 juta penduduk dan anak -anak 1 tahun?

9 = 10 - 1 = μ - s

11 = 10 + 1 = μ + s

Oleh itu: [9, 11] = [μ - s, μ + s]

Menurut peraturan empirikal, 68.27% daripada satu kanak -kanak -kanak -kanak yang berada dalam selang waktu [μ -s, μ + s]

Di negara ini terdapat 500,000 kanak -kanak satu tahun (1% daripada 50 juta), jadi 341350 kanak -kanak (68.27% daripada 500000) mempunyai berat antara 9 dan 11 kilogram.

Rujukan

1. Abraira, v. (2002). Sisihan piawai dan ralat standard. Majalah Semergen. Web pulih.Arkib.org.
2. Freund, r.; Wilson, w.; Mohr, d. (2010). Kaedah statistik. Ketiga ed. Akademik Press-Essevier Inc.
3. Pelayan Alicante (2017). Peraturan empirikal (istilah statistik). Glosari pulih.pelayan-Alive.com.
4. Lind, d.; Marchal, w.; Wathen, s. (2012). Statistik digunakan untuk perniagaan dan ekonomi. Kesepuluh ed. McGraw-Hill/Inter-American dari Mexico S. Ke.
5. Salinas, h. (2010). Statistik dan kebarangkalian. Pulih dari UDA.Cl.
6. Sokal, r.; Rohlf, f. (2009). Pengenalan kepada Biostatistik. Kedua ed. Penerbitan Dover, Inc.
7. Spiegel, m. (1976). Kebarangkalian dan statistik. Siri Schaum. McGraw-Hill/Inter-American dari Mexico S. Ke.
8. Spiegel, m.; Stephens, l. (2008). Statistik. Ed keempat. McGraw-Hill/Inter-American dari Mexico S. Ke.
9. Kajian STAT119 (2019). Soalan peraturan penyelesaian empirikal. Diperolehi daripada STAT119Review.com.
10. (2019). 68-95-99.7 Peraturan. Diambil dari.Wikipedia.org.