Konsep percubaan rawak, ruang sampel, contoh

Ada ceramah Percubaan rawak Apabila hasil setiap percubaan tertentu tidak dapat diramalkan, walaupun kebarangkalian terjadinya hasil tertentu dapat diwujudkan.

Walau bagaimanapun, perlu dijelaskan bahawa tidak mungkin untuk menghasilkan semula hasil yang sama dari sistem rawak dengan parameter dan keadaan awal yang sama dalam setiap percubaan eksperimen.

Rajah 1. Pelancaran Dadu adalah percubaan rawak. Sumber: Pixabay.

Contoh yang baik dari percubaan rawak adalah pelancaran dadu. Walaupun anda berhati -hati untuk melancarkan dadu dengan cara yang sama, dalam setiap percubaan hasil yang tidak dapat diramalkan akan diperolehi. Sebenarnya, satu -satunya perkara yang boleh disahkan ialah hasilnya boleh menjadi beberapa perkara berikut: 1, 2, 3, 4, 5 atau 6.

Pelancaran mata wang adalah satu lagi contoh percubaan rawak dengan hanya dua hasil yang mungkin: muka atau meterai. Walaupun mata wang dilancarkan dari ketinggian yang sama dan dengan cara yang sama, faktor peluang akan sentiasa hadir, yang mengakibatkan ketidakpastian untuk setiap percubaan baru.

Kebalikan dari eksperimen rawak adalah percubaan deterministik. Sebagai contoh, diketahui bahawa setiap masa air direbus di paras laut suhu mendidih adalah 100 ºC. Tetapi tidak pernah berlaku, mengekalkan keadaan yang sama, hasilnya kadang -kadang 90 ºC, 12 0 ºC dan kadang -kadang 100 ºC.

[TOC]

Ruang sampel

Set semua kemungkinan hasil percubaan rawak dipanggil ruang sampel. Dalam percubaan rawak pelancaran dadu, ruang sampel adalah:

D = 1, 2, 3, 4, 5, 6.

Bagi bahagiannya, pada pelancaran mata wang ruang sampel adalah:

M = muka, meterai.

Acara atau acara

Dalam eksperimen rawak, a peristiwa Itu adalah kejadian atau tidak hasil tertentu. Contohnya, dalam hal pelancaran mata wang, acara atau acara adalah mahal.

Boleh melayani anda: sisi homolog

Satu lagi peristiwa dalam percubaan rawak boleh seperti berikut: bahawa pada pelancaran dadu nombor kurang daripada tiga dibebaskan.

Sekiranya peristiwa berlaku, maka set hasil yang mungkin adalah set:

E = 1, 2, 3

Sebaliknya, ini adalah subset ruang atau set sampel:

M = 1, 2, 3, 4, 5, 6.

Contoh

Berikut adalah beberapa contoh yang menggambarkan perkara di atas:

Contoh 1

Menganggap bahawa dua duit syiling dilemparkan, satu demi satu. Ia diminta:

a) Tunjukkan sama ada ia adalah percubaan rawak atau sebaliknya percubaan deterministik.

b) Apakah ruang sampel percubaan ini?

c) Nyatakan keseluruhan peristiwa A, sepadan dengan eksperimen mempunyai wajah dan hasil setem.

d) mengira kebarangkalian bahawa peristiwa berlaku pada.

e) Akhirnya, cari kebarangkalian bahawa peristiwa b: tidak kelihatan wajah dengan hasilnya.

Penyelesaian 

a) Ini adalah percubaan rawak kerana tidak ada cara untuk meramalkan apa yang akan menjadi hasil pelancaran dua syiling.

b) Ruang sampel adalah set semua hasil yang mungkin:

S = (c, c), (c, s), (s, c), (s, s)

c) Peristiwa A, dalam kes yang diberikan, boleh mempunyai hasil berikut:

A = (c, s), (s, c)

d) Kebarangkalian peristiwa A diperolehi daripada membahagikan bilangan unsur set A antara bilangan unsur set yang sepadan dengan ruang sampel:

P (a) = 2/4 = ½ = 0.5 = 50%

e) set hasil yang mungkin bersamaan dengan peristiwa b (tidak muncul muka kepada hasilnya) adalah:

Boleh melayani anda: trinomial persegi sempurna

B = (s, s)

Oleh itu, kebarangkalian bahawa peristiwa B berlaku dalam esei adalah nisbah antara jumlah hasil yang mungkin dari b antara jumlah kes:

P (b) = ¼ = 0.25 = 25%.

Contoh 2

Beg mengandungi 10 guli putih dan 10 guli hitam. Dari beg mereka dikeluarkan secara rawak dan tanpa melihat ke dalam tiga guli berturut -turut. 

a) Tentukan ruang sampel percubaan rawak ini.

b) Tentukan set hasil yang sepadan dengan peristiwa yang selepas eksperimen terdapat dua kelereng hitam.

c) Acara B adalah untuk mendapatkan sekurang -kurangnya dua kelereng hitam, tentukan set B hasil untuk acara ini.

d) Apakah kebarangkalian peristiwa itu berlaku?

e) Cari kebarangkalian peristiwa b.

f) Tentukan kebarangkalian bahawa hasil percubaan rawak adalah sekurang -kurangnya satu marmar hitam. Acara ini akan dipanggil c.

Rajah 2. Kelereng hitam dan hitam untuk eksperimen rawak. Sumber: NeedPix.

Penyelesaian kepada

Untuk membina ruang sampel, adalah berguna untuk membuat gambarajah pokok, seperti yang ditunjukkan dalam Rajah 3:

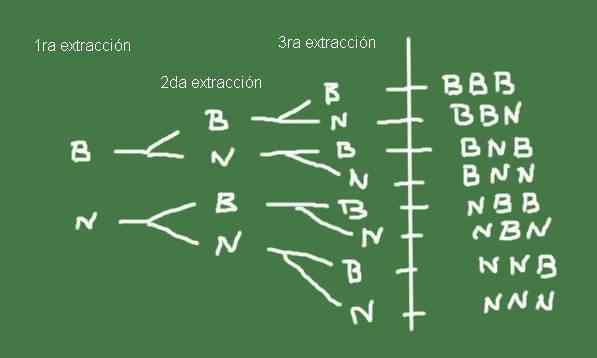Rajah 3. Rajah pokok misalnya 2. Disediakan oleh fanny zapata.

Set ω hasil yang mungkin mengekstrak tiga guli dari beg dengan jumlah kelereng hitam dan hitam yang sama, adalah tepat ruang sampel percubaan rawak ini.

Ω = (b, b, b), (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n) , (n, n, b), (n, n, n)

Penyelesaian b

Set hasil yang mungkin bersamaan dengan peristiwa A, yang terdiri daripada mempunyai dua guli hitam adalah:

Boleh melayani anda: Jumlah Riemann: Sejarah, Formula dan Properties, Latihan

A = (b, n, n), (n, b, n), (n, n, b)

Penyelesaian c

Acara B ditakrifkan sebagai: "mempunyai sekurang -kurangnya dua kelereng hitam setelah membuat pengekstrakan rawak tiga daripadanya". Set hasil yang mungkin untuk acara B ialah:

B = (b, n, n), (n, b, n), (n, n, b), (n, n, n)

Penyelesaian d

Kebarangkalian mempunyai peristiwa A adalah nisbah antara jumlah hasil yang mungkin untuk acara ini, dan jumlah hasil yang mungkin, iaitu bilangan elemen ruang sampel.

P (a) = n (a) / n (ω) = 3/8 = 0.375 = 37.5%

Jadi ada 37.Kebarangkalian 5% mempunyai dua kelereng hitam selepas secara rawak diekstrak tiga guli dari beg. Tetapi ambil perhatian bahawa tidak semestinya kita dapat meramalkan hasil yang tepat dari eksperimen.

Penyelesaian e

Kebarangkalian bahawa peristiwa B diberikan, yang terdiri daripada sekurang -kurangnya satu marmar hitam adalah:

P (b) = n (b) / n (ω) = 4/8 = 0.5 = 50%

Ini bermaksud bahawa kemungkinan peristiwa B sama dengan kebarangkalian yang tidak berlaku. 

Penyelesaian f

Kebarangkalian mendapatkan sekurang -kurangnya satu marmar hitam, setelah mengekstrak tiga daripadanya, sama dengan 1 kurang kebarangkalian hasilnya adalah "tiga guli putih".

P (c) = 1 - p (b b b) = 1 - ⅛ = ⅞ = 0.875 = 87.5%

Sekarang, kita dapat mengesahkan hasil ini, dengan menyatakan bahawa bilangan kemungkinan yang diberikan peristiwa C adalah sama dengan bilangan unsur hasil yang mungkin untuk peristiwa c:

C = (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n), (n, n, b) , (n, n, n)

N (c) = 7

P (c) = n (c) / n (ω) = ⅞ = 87.5%

Rujukan

1. Canalphi. Percubaan rawak. Pulih dari: youtube.com.
2. Mathemovil. Percubaan rawak. Pulih dari: youtube.com
3. Pishro Nick h . Pengenalan kepada kebarangkalian. Diperolehi daripada: ProbabilityCourse.com
4. Ross. Kebarangkalian dan statistik untuk jurutera. Mc-Graw Hill.
5. Wikipedia. Eksperimen (teori kebarangkalian). Diperoleh dari: dalam.Wikipedia.com
6. Wikipedia. Peristiwa deterministik. Pulih dari: Adakah. Wikipedia.com
7. Wikipedia. Percubaan rawak. Pulih dari: Adakah.Wikipedia.com