Formula pengedaran hypergeometric, persamaan, model

The Pengagihan Hypergeometric Ia adalah fungsi statistik yang bijak, mencukupi untuk mengira kebarangkalian dalam eksperimen rawak dengan dua hasil yang mungkin. Keadaan yang diperlukan untuk memohon adalah bahawa ia adalah populasi kecil, di mana pengekstrakan tidak diganti dan kebarangkalian tidak tetap. 

Oleh itu, apabila elemen penduduk dipilih untuk mengetahui hasilnya (benar atau palsu) dari ciri tertentu, unsur yang sama tidak dapat dipilih lagi.

Rajah 1. Dalam populasi skru seperti ini, pasti ada spesimen yang cacat. Sumber: Pixabay.

Sudah tentu, elemen seterusnya yang dipilih adalah lebih cenderung untuk mendapatkan hasil yang benar, jika elemen sebelumnya mempunyai hasil negatif. Ini bermaksud bahawa kebarangkalian berbeza -beza, setakat unsur -unsur sampel diekstrak.

Aplikasi utama pengedaran hypergeometric adalah: kawalan kualiti dalam proses dengan sedikit populasi dan pengiraan kebarangkalian dalam permainan rawak.

Bagi fungsi matematik yang mentakrifkan taburan hipergeometrik, ini terdiri daripada tiga parameter, iaitu:

- Nombor Unsur Penduduk (n)

- Saiz sampel (m) 

- Bilangan peristiwa dalam populasi yang lengkap dengan hasil yang baik (atau tidak menguntungkan) dari ciri yang dikaji (n).

[TOC]

Formula dan persamaan

Formula pengedaran hipergeometrik memberikan kebarangkalian P tentang apa x kes -kes yang menggalakkan ciri -ciri tertentu berlaku. Cara menulisnya secara matematik, bergantung kepada nombor gabungan adalah:

Dalam ungkapan sebelumnya N, n dan m Mereka adalah parameter dan x pembolehubah itu sendiri. 

-Jumlah penduduk adalah N.

-Bilangan hasil positif dari ciri binari tertentu berkenaan dengan jumlah penduduk adalah n.

-Bilangan elemen sampel adalah m.

Dalam kes ini, X Ia adalah pemboleh ubah rawak yang memerlukan nilai x dan P (x) menunjukkan kebarangkalian kejadian x kes -kes yang menggalakkan ciri -ciri yang dikaji.

Pembolehubah statistik penting

Pembolehubah statistik lain untuk pengedaran hypergeometric adalah:

- Separuh μ = m*n/n

- Varians σ^2 = m*(n/n)*(1-n/n)*(n-m)/(n-1)

- Penyimpangan biasa σ yang merupakan akar kuadrat dari varians.

Model dan sifat 

Untuk sampai ke model pengedaran hypergeometric, ia berdasarkan kebarangkalian mendapatkan x kes yang menggalakkan dalam sampel saiz m. Sampel ini mengandungi unsur -unsur yang memenuhi harta di bawah kajian dan unsur -unsur yang tidak.

Mari kita ingat bahawa n mewakili bilangan kes yang menggalakkan dalam jumlah penduduk N Item. Maka kebarangkalian akan dikira seperti ini:

Boleh melayani anda: ruang vektor: asas dan dimensi, aksioma, sifat

P (x) = (# cara untuk mendapatkan x# dengan cara yang gagal)/(# Jumlah cara memilih)

Mengekspresikan perkara di atas dalam bentuk nombor gabungan, model pengedaran kebarangkalian berikut dicapai:

Sifat utama pengedaran hypergeometric

Adalah perkara berikut:

- Sampel mesti selalu kecil, walaupun penduduknya besar.

- Unsur -unsur sampel diekstrak dari satu, tanpa memasukkannya lagi ke dalam populasi.

- Harta yang akan dikaji adalah binari, iaitu, ia hanya boleh mengambil dua nilai: 1 Sama ada 0, Wahai Benar Sama ada palsu.

Dalam setiap langkah pengekstrakan langkah, kebarangkalian berubah bergantung pada hasil sebelumnya.

Pendekatan dengan pengedaran binomial

Satu lagi harta pengedaran hypergeometric adalah bahawa ia boleh didekati oleh pengedaran binomial, dilambangkan sebagai Bi, selagi penduduk N Jadilah besar dan sekurang -kurangnya 10 kali lebih besar daripada sampel m. Dalam kes ini ia akan menjadi seperti ini:

P (n, n, m; x) = bi (m, n/n, x)           

Selagi n besar dan n> 10m

Contoh

Contoh 1

Katakan mesin yang menghasilkan skru dan data terkumpul menunjukkan bahawa 1% keluar dengan kecacatan. Kemudian dalam kotak n = 500 skru bilangan kecacatan akan:

N = 500 * 1/100 = 5

Kebarangkalian melalui pengedaran hypergeometric

Katakan bahawa dari kotak itu (iaitu, penduduk itu) kita mengambil sampel m = 60 skru.

Kebarangkalian bahawa tiada skru (x = 0) sampel daun cacat ialah 52.63%. Hasil ini dicapai apabila menggunakan fungsi pengedaran hypergeometric:

P (500, 5, 60; 0) = 0.5263

Kebarangkalian bahawa x = 3 skru sampel meninggalkan cacat ialah: P (500, 5, 60; 3) = 0.0129.

Sebaliknya, kebarangkalian bahawa x = 4 skru dari enam puluhan sampel cuti yang rosak adalah: P (500, 5, 60; 4) = 0.0008.

Akhirnya, kebarangkalian bahawa x = 5 skru dalam sampel itu keluar dengan kecacatan adalah: p (500, 5, 60; 5) = 0.

Tetapi jika anda ingin mengetahui kebarangkalian bahawa dalam sampel itu terdapat lebih daripada 3 skru yang cacat, maka kebarangkalian terkumpul mesti diperoleh, menambah:

P (3)+P (4)+P (5) = 0.0129+0.0008+0 = 0.0137.

Contoh ini digambarkan dalam Rajah 2, yang diperoleh melalui penggunaan Geogebra Perisian Percuma Gunakan luas di sekolah, institusi dan universiti.

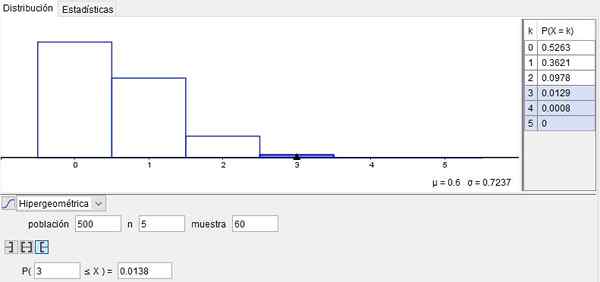Rajah 2. Contoh pengedaran hypergeometric. Disediakan oleh f. Zapata dengan geogebra.

Contoh 2

Dek dek Sepanyol mempunyai 40 kad, yang mana 10 mempunyai emas dan baki 30 tidak memilikinya. Katakan 7 kad diekstrak dari dek itu, yang tidak kembali ke dek.

Boleh melayani anda: simetri pusat: sifat, contoh dan latihan

Jika x adalah bilangan emas yang terdapat dalam 7 kad yang diekstrak, maka kebarangkalian X oros dalam pengekstrakan 7 kad diberikan oleh pengedaran hypergeometric p (40,10,7; x).

Mari kita lihat ini: Untuk mengira kebarangkalian mempunyai 4 emas dalam pengekstrakan 7 kad kita menggunakan formula pengedaran hypergeometric dengan nilai berikut:

Dan hasilnya ialah: kebarangkalian 4.57%.

Tetapi jika anda ingin mengetahui kebarangkalian mendapatkan lebih daripada 4 kad, maka kami perlu menambah:

P (4)+P (5)+P (6)+P (7) = 5.20%

Latihan yang diselesaikan

Set latihan berikut dimaksudkan untuk menggambarkan dan mengasimilasikan konsep yang telah dibentangkan dalam artikel ini. Adalah penting bahawa pembaca cuba menyelesaikannya sendiri, sebelum melihat penyelesaiannya.

Latihan 1

Kilang profilaksis telah mendapati bahawa setiap 1000 kondom yang dihasilkan oleh mesin tertentu, 5 adalah cacat. Untuk menjalankan kawalan kualiti, 100 kondom diambil secara rawak dan lot ditolak jika terdapat sekurang -kurangnya satu atau lebih yang rosak. Balas:

a) Kemungkinan apa yang mesti dibuang 100 lot?

b) Adakah kriteria kawalan kualiti ini cekap?

Penyelesaian

Dalam kes ini nombor gabungan yang sangat besar akan muncul. Pengiraannya sukar, melainkan jika pakej komputer yang mencukupi tersedia.

Tetapi kerana ia adalah populasi yang besar dan sampelnya sepuluh kali kurang daripada jumlah penduduk, anda boleh menggunakan pendekatan untuk pengedaran hipergeometrik kerana pengedaran binomial:

P (1000,5,100; x) = BI (100, 5/1000, x) = BI (100, 0.005, x) = c (100, x)*0.005^x (1-0.005)^(100-x)

Dalam ungkapan sebelumnya C (100, x) Ia adalah nombor kombinatorial. Kemudian kebarangkalian Haya lebih daripada satu cacat akan dikira seperti berikut:

P (x> = 1) = 1 - bi (0) = 1-.6058 = 0.3942

Ia adalah pendekatan yang sangat baik, jika dibandingkan dengan nilai yang diperoleh apabila menggunakan taburan hypergeometric: 0.4102

Boleh dikatakan bahawa, kebarangkalian 40% banyak 100 profilaktik harus dibuang, yang tidak begitu efisien.

Tetapi, sedikit kurang menuntut dalam proses kawalan kualiti dan membuang.

Latihan 2

Mesin taco plastik berfungsi sedemikian rupa sehingga setiap 10 keping, satu cacat. Dalam sampel 5 -bahagian yang kemungkinan mesti menjadi satu bahagian yang rosak.

Penyelesaian

Penduduk: n = 10

Boleh melayani anda: Identiti Pythagorean: Demonstrasi, Contoh, Latihan

Nombor n cacat bagi setiap n: n = 1

Saiz Contoh: M = 5

P (10, 1, 5; 1) = C (1.1)*C (9.4)/C (10.5) = 1*126/252 = 0.5

Oleh itu terdapat kebarangkalian 50% bahawa dalam sampel 5, taco keluar cacat.

Latihan 3

Dalam mesyuarat sekolah menengah muda terdapat 7 wanita dan 6 lelaki. Antara gadis, 4 kajian kemanusiaan dan 3 sains. Dalam kumpulan lelaki, 1 kajian kemanusiaan dan 5 sains. Kirakan perkara berikut:

a) secara rawak memilih tiga gadis: apakah kebarangkalian semua mempelajari kemanusiaan?.

b) Jika tiga peserta dipilih secara rawak untuk mesyuarat kawan -kawan: apakah tiga dari mereka, tanpa mengira seks, belajar tiga, atau kemanusiaan juga ketiga -tiga?.

c) Sekarang pilih dua rakan rawak dan hubungi x kepada pemboleh ubah rawak "bilangan mereka yang mempelajari kemanusiaan". Antara yang dipilih, tentukan nilai purata atau jangkaan x dan varians σ^2.

Penyelesaian kepada 

Penduduk adalah jumlah gadis: n = 7. Yang mempelajari kemanusiaan adalah n = 4, dari jumlah. Sampel rawak gadis akan menjadi m = 3.

Dalam hal ini, kebarangkalian bahawa ketiga -tiga adalah kemanusiaan diberikan oleh fungsi hypergeometric:

P (n = 7, n = 4, m = 3, x = 3) = C (4, 3) C (3, 0) / C (7, 3) = 0.1143

Kemudian ada 11.Kebarangkalian 4% bahawa tiga kemanusiaan kajian chicas rawak.

Penyelesaian b

Nilai yang akan digunakan adalah:

-Penduduk: n = 14

-Kuantiti yang mengkaji huruf ialah: n = 6 dan

-Saiz sampel: m = 3.

-Bilangan rakan yang mempelajari kemanusiaan: x

Menurut ini, x = 3 bermaksud bahawa ketiga -tiga kajian kemanusiaan, tetapi x = 0 bermaksud tidak ada kajian kemanusiaan. Kebarangkalian bahawa ketiga -tiga kajian yang sama diberikan oleh jumlah:

P (14, 6, 3, x = 0) + P (14, 6, 3, x = 3) = 0.0560 + 0.1539 = 0.2099

Kemudian, kami mempunyai kebarangkalian 21% bahawa tiga peserta mesyuarat, dipilih secara rawak, mengkaji sama.

Penyelesaian c

Di sini kita mempunyai nilai berikut:

N = 14 jumlah penduduk kawan, n = 6 jumlah jumlah dalam populasi yang mengkaji kemanusiaan, saiz sampel adalah m = 2.

Harapan adalah:

E (x) = m * (n/n) = 2 * (6/14) = 0.8572

Dan varians:

σ (x)^2 =  m*(n/n)*(1-n/n)*(n-m)/(n-1) = 2*(6/14)*(1-6/14)*(14-2)/(14 -1) =

= 2*(6/14)*(1-6/14)*(14-2)/(14-1) = 2*(3/7)*(1-3/7)*(12) (13)  = 0.4521

Rujukan

1. Pengagihan kebarangkalian diskret. Pulih dari: biple.usal.adalah
2. Statistik dan kebarangkalian. Pengagihan Hypergeometric. Diperolehi daripada: ProjectodeScartes.org
3. Cdpye-ugr. Pengagihan Hypergeometric. Pulih dari: ugr.adalah
4. Geogebra. Geogebra klasik, pengiraan kebarangkalian. Pulih dari geogebra.org
5. Probate mudah. Latihan pengedaran hipergeometrik yang diselesaikan. Pulih dari: probafacil.com
6. Minitab. Pengagihan Hypergeometric. Diperolehi dari: Sokongan.Minitab.com
7. Universiti Vigo. Pengagihan diskret utama. Pulih dari: ANAPG.laman web.Uvigo.adalah
8. Vitutor. Statistik dan kombinatorial. Diperolehi daripada: Vitutor.jaring
9. Weisstein, Eric W. Pengagihan Hypergeometric. Pulih dari: Mathworld.Wolfram.com
10. Wikipedia. Pengagihan Hypergeometric. Pulih dari: Adakah.Wikipedia.com