Formula induksi magnet, bagaimana ia dikira dan contohnya

The induksi magnet atau ketumpatan fluks magnet adalah perubahan persekitaran yang disebabkan oleh kehadiran arus elektrik. Mereka mengubah sifat ruang sekitar, mewujudkan a medan Vektor.

Vektor Induksi magnet, ketumpatan fluks magnet Atau semata -mata medan magnet B, Ia mempunyai tiga ciri tersendiri: intensiti yang dinyatakan oleh nilai berangka, alamat dan juga rasa yang diberikan pada setiap titik di ruang angkasa. Ia diketengahkan dengan berani untuk membezakannya dari jumlah atau skalar semata -mata.

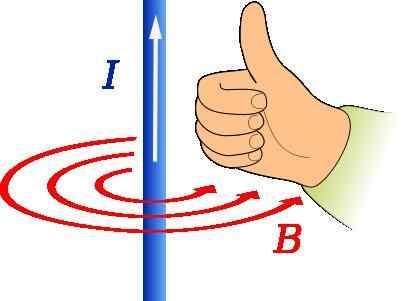Peraturan ibu jari kanan untuk menentukan arah dan arah vektor induksi magnet. Sumber: JFMelero [CC BY-SA 4.0 (https: // creativeCommons.Org/lesen/by-sa/4.0)]

Peraturan ibu jari kanan digunakan untuk mencari arah dan arah medan magnet yang berasal dari dawai yang mengangkut arus, seperti yang ditunjukkan dalam angka di atas.

Ibu jari tangan kanan harus menunjuk ke arah arus. Kemudian giliran jari yang tinggal menunjukkan bentuk B, bahawa dalam angka itu diwakili oleh lingkaran sepusat merah.

Dalam kes ini, alamat B Ia adalah tangen ke lilitan sepusat dengan wayar dan makna bertentangan dengan tangan jam.

The induksi magnet B Dalam sistem antarabangsa Tesla (T) diukur, namun lebih biasa untuk mengukurnya di unit lain yang dipanggil Gauss (G). Kedua-dua unit dilantik masing-masing sebagai penghormatan kepada Nikola Tesla (1856-1943) dan Carl Friedrich Gauss (1777-1855) atas sumbangan luar biasa mereka kepada sains elektrik dan magnetisme.

[TOC]

Apakah sifat induksi magnet atau ketumpatan fluks magnet?

Kompas yang diletakkan berhampiran dawai dengan arus, akan selalu selari dengan B. Fizik Denmark Hans Christian Oersted (1777-1851) adalah yang pertama menyedari fenomena ini pada awal abad ke-19.

Boleh melayani anda: kelajuan isolar: bagaimana ia dikira dan diselesaikan latihan

Dan apabila semasa berhenti, kompas menunjuk ke utara geografi, seperti biasa. Dengan berhati -hati mengubah kedudukan kompas, peta diperoleh dari bentuk medan magnet.

Peta ini selalu mempunyai bentuk bulatan sepusat ke dawai, seperti yang diterangkan pada mulanya. Dengan cara ini ia dapat digambarkan B.

Walaupun wayar tidak lurus, vektor B akan membentuk bulatan sepusat di sekelilingnya. Untuk menentukan bentuk medan apa, sudah cukup untuk membayangkan segmen dawai yang sangat kecil, begitu kecil sehingga mereka kelihatan rectilinear dan dikelilingi oleh lilitan sepusat.

Garis medan magnet yang dihasilkan oleh gelung dawai yang mengangkut arus. Sumber: Pixabay.com

Ini menunjukkan harta penting dari garis medan magnet B: Mereka tidak mempunyai prinsip atau akhir, mereka selalu lekuk tertutup.

Undang-undang Biot-Savart

Abad kesembilan belas menentukan permulaan era elektrik dan magnet dalam sains. Berhampiran tahun 1820 ahli fizik Perancis Jean Marie Biot (1774-1862) dan Felix Savart (1791-1841) menemui undang-undang yang menanggung namanya dan yang membolehkan mengira vektor B.

Mereka membuat pemerhatian berikut mengenai sumbangan kepada medan magnet yang dihasilkan oleh segmen wayar panjang pembezaan dl yang mengangkut arus elektrik Yo:

• Magnitud B berkurangan dengan songsang ke kuadrat jarak ke dawai (ini masuk akal: jauh dari dawai keamatan B Ia mesti kurang dari di tempat berdekatan).
• Magnitud B Ia berkadar dengan intensiti arus Yo yang bergerak di kawat.
• Alamat B Ia adalah tangen ke lilitan radio r berpusat pada wayar dan arah B Ia diberikan, seperti yang kita katakan, oleh peraturan ibu jari yang betul.

Produk silang vektor atau produk adalah alat matematik yang sesuai untuk menyatakan titik terakhir. Untuk menubuhkan produk vektor, dua vektor diperlukan, yang ditakrifkan seperti berikut:

• dL Ia adalah vektor yang magnitudnya adalah panjang segmen pembezaan dl
• r Ia adalah vektor yang pergi dari dawai ke titik di mana anda ingin mencari medan

Boleh melayani anda: Spektrum Elektromagnetik: Ciri, Band, Aplikasi

Formula

Semua ini boleh digabungkan dalam ungkapan matematik:

Perkadaran yang berterusan yang diperlukan untuk mewujudkan kesamaan adalah Kebolehtelapan magnet ruang bebas μ_{Sama ada}  = 4π.10^-7 T.m/a

Ungkapan ini adalah undang -undang Biot dan Savart, yang membolehkan anda mengira medan magnet segmen semasa.

Segmen sedemikian pula mestilah sebahagian daripada litar yang lebih besar dan lebih besar: taburan semasa.

Keadaan litar ditutup diperlukan untuk arus elektrik mengalir. Arus elektrik tidak dapat mengalir dalam litar terbuka.

Akhirnya, untuk mencari medan magnet keseluruhan pengedaran semasa ini, semua sumbangan setiap segmen pembezaan ditambah dL. Ini bersamaan dengan mengintegrasikan semua pengedaran:

Untuk memohon undang-undang Biot-Savart dan mengira vektor induksi magnet, adalah perlu untuk mempertimbangkan perkara penting yang sangat penting:

• Produk vektor antara dua vektor selalu menghasilkan vektor lain.
• Besarnya produk vektor dalam undang-undang Biot-Savart adalah:di mana θ adalah sudut antara dL dan r.
• Produk vektor harus dijumpai sebelumnya Sekiranya resolusi penting diselesaikan, maka integral setiap komponen yang diperoleh secara berasingan diselesaikan.
• Adalah perlu untuk menarik keadaan dan mewujudkan sistem koordinat yang mencukupi.
• Apabila kewujudan beberapa simetri diperhatikan, ia mesti digunakan untuk menjimatkan masa pengiraan.
• Apabila terdapat segitiga, teorem pythagoras dan teorem kosinus sangat membantu untuk mewujudkan hubungan geometri antara pembolehubah.

Bagaimana ia dikira?

Dengan contoh praktikal pengiraan B Untuk dawai rectilinear, cadangan ini digunakan.

Ia boleh melayani anda: beban tepat waktu: sifat dan undang -undang coulomb

Contoh

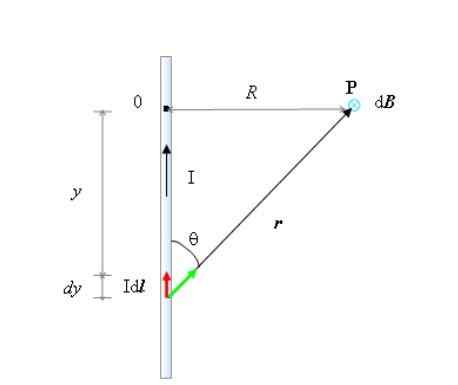
Kirakan vektor medan magnet yang menghasilkan dawai rectilinear yang sangat panjang pada titik P ruang, menurut angka yang ditunjukkan.

Geometri yang diperlukan untuk mengira medan magnet pada titik p, dari wayar semasa yang tidak terhingga. Sumber: Diri Diri.

Dari angka yang anda harus:

• Kawat diarahkan secara menegak, dengan arus saya mengalir. Alamat ini +dan dalam sistem koordinat, yang asalnya berada pada titik atau.
• θ adalah sudut antara dL dan r Dan juga benar bahawa: 
• Dalam kes ini, mengikut peraturan ibu jari kanan, B Pada titik p diarahkan ke dalam kertas, jadi ia dilambangkan dengan bulatan kecil dan "x" dalam angka itu. Alamat ini akan diambil sebagai -z.
• Segitiga kanan yang kakinya dan dan R, mengaitkan kedua -dua pembolehubah mengikut teorem Pythagoras: r²= R²+dan²

Semua ini digantikan dengan integral. Produk vektor atau silang ditunjukkan oleh magnitudnya ditambah arah dan maknanya:

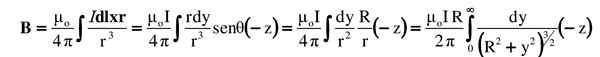
Integral yang dicadangkan dicari dalam jadual penting atau diselesaikan oleh penggantian trigonometri yang sesuai (pembaca dapat memeriksa hasilnya menggunakan y = rtg θ):

Hasilnya bersetuju dengan yang diharapkan: magnitud medan berkurangan dengan jarak r dan meningkat secara proporsional dengan intensiti semasa i.

Walaupun dawai yang tidak terhingga adalah idealisasi, ungkapan yang diperoleh adalah pendekatan yang sangat baik untuk bidang dawai panjang.

Dengan undang -undang Biot dan Savart, mungkin untuk mencari medan magnet pengagihan simetri tinggi yang lain, seperti lingkaran bulat yang mengangkut wayar semasa, atau dilipat menggabungkan segmen rectilinear dan curvilinear.

Sudah tentu, untuk menganalisis yang penting, masalahnya mesti mempunyai tahap simetri yang tinggi. Jika tidak, alternatifnya secara berangka menyelesaikan masalah.

Rujukan

1. Serway, r., Jewett, J. (2008). Fizik untuk Sains dan Kejuruteraan. Jilid 2. Mexico. Editor Pembelajaran Cengage. 367-372.