Interpolasi LaGrange

Apakah interpolasi LaGrange?

Interpolasi LaGrange adalah kaedah berangka penghampiran fungsi, yang menggunakan polinomial yang melewati titik tertentu yang diketahui dari fungsi yang bertujuan untuk menghampiri.

Sekiranya fungsi anggaran lembut, walaupun di luar nilai yang diberikan atau diketahui, polinomial mengambil nilai -nilai yang dekat dengan fungsi kepentingan, terutamanya jika nilai -nilai ini adalah antara titik yang diberikan. Itulah sebabnya polinomial dianggap sebagai pendekatan yang baik untuk fungsi.

Rajah 1.- Formula untuk membina polinomial lagrange. Sumber: f. Zapata.

Sekarang, katakan anda ingin menghampiri fungsi f (x) yang mana hanya nilai mereka yang diketahui dalam beberapa x-_Yo-, dengan Yo dari 0 sehingga N-1. Iaitu, mereka saling mengenali n Mata (x-_Yo, dan_Yo) dengan dan_Yo = f (x_Yo), Di mana indeks Yo Pergi dari 0 sehingga N-1.

Dalam kaedah interpolasi LaGrange, polinomial yang mendekati fungsi f (x) Ia adalah polinomial P (x) ijazah N-1, dibina oleh gabungan linear dari n Polinomial L_Yo(x) ijazah N-1. Ini adalah Lagrange Polynomials, yang dinyatakan seperti berikut:

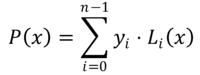
Nilai -nilai dan_Yo Mereka mewakili ordinat yang sepadan dengan abscissa x_Yo Di mana fungsi f (x) Ia diketahui, iaitu: dan_Yo = f (x_Yo).

Lagrange Polynomials

Melalui kombinasi linear di antara mereka, polinomial LaGrange bertindak sebagai asas untuk membina polinomial gred N -1 yang akan berfungsi untuk menginterpolasi n mata yang diketahui.

Notasi untuk polinomial adalah l_Yo(x), dengan indeks I dalam julat dari 0 hingga n-1. Formula untuk menubuhkan polinomial LaGrange adalah seperti berikut:

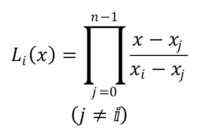
Simbol yang ditunjukkan menunjukkan bahawa produksi n -1 monomial mesti dilakukan, bermula dari polinomial j = 0.

Ciri -ciri polinomial LaGrange

1.- Polinomial LaGrange sama persis dengan unit apabila dinilai di abscissa yang sepadan dengan indeks mereka, iaitu:

L_Yo(x_Yo) = 1

2.- Mereka dibatalkan di abscissa titik interpolasi dengan indeks berbeza daripada polinomial yang sama:

Boleh melayani anda: Statistik deskriptif: sejarah, ciri, contoh, konsep

L_Yo(x_J) = 0, dengan i ≠ j.

3.- Mengambil nilai abscissa yang lain berbeza dari titik interpolasi, polinomial LaGrange memperoleh nilai antara -1 dan +1.

4.- Untuk mendapatkan polinomial LaGrange, hanya perlu mengetahui abscissa mata untuk interpoch.

Polinomial LaGrange yang kedua

Polinomial Lagrange kedua adalah yang paling kerap digunakan apabila anda ingin melakukan interpolasi tiga titik.

Katakan fungsi interpolar diketahui dalam tiga mata, iaitu:

(x₀,dan₀); (x₁, dan₁); (x₂, dan₂)

Kemudian polinomial LaGrange yang sesuai L₀, L₁ dan L₂ Mereka menjadi seperti ini:

L₀(x) = [(x - x₁) / (X₀ - x₁)] [(x - x₂) / (X₀ - x₂)]

L₁(x) = [(x - x₀) / (X₁ - x₀)] [(x - x₂) / (X₁ - x₂)]

L₂(x) = [(x - x₀) / (X₂ - x₀)] [(x - x₁) / (X₂ - x₁)]

Harus diperhatikan bahawa L₀(x₀) = L₁(x₁) = L₂(x₂) = 1, manakala L_Yo(x_J) = 0 selagi Yo≠ j.

Polinomial interpolasi darjah kedua

Adalah penting untuk diperhatikan bahawa dalam polinomial interpolasi LaGrange, ordinan titik interpolasi adalah faktor polinomial LaGrange.

Dengan cara ini, apabila polinomial diperolehi untuk nilai -nilai tertentu abscissa, mereka berfungsi untuk mengira polinomial interpolasi pelbagai fungsi, dengan syarat bahawa yang diperintahkan dalam abscissa yang telah ditetapkan sebelumnya diketahui diketahui.

Dalam kes interpolasi gred kedua:

P (x) = f (x₀) L₀(x) + f (x₁) L₁(x) + f (x₂) L₂(x)

Dan p (x) mendekati fungsi f (x) dalam selang waktu (x₀, x₂).

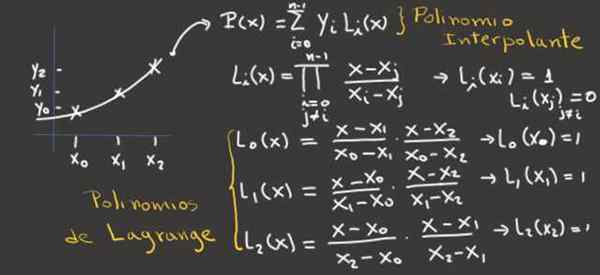Rajah 2.- Imej ini menunjukkan bagaimana untuk mendapatkan polinomial Lagrange untuk tiga titik interpolasi dan dari mereka, polinomial interpoling. Sumber: f. Zapata.

Contoh

Contoh 1

Cari polinomial LaGrange yang sepadan dengan tiga mata abscissa x₀= 0, x₁= 1 dan x₂= 2.

Seperti yang dilihat di bahagian sebelumnya, polinomial ini akan menjadi:

Boleh melayani anda: Fungsi overjective: definisi, sifat, contoh

L₀(x) = [(x - 1) / (0 - 1)] [(x - 2) / (0 - 2)] = - (x -1) ⋅ (-½) (x - 2) = ½ ( x² - 3x + 2)

L₁(x) = [(x - 0) / (1 - 0)] [(x - 2) / (1 - 2)] = x ⋅ (-1) (x - 2) = - x² + 2x

L₂(x) = [(x - 0) / (2 - 0)] [(x - 1) / (2 - 1)] = (½) x ⋅ (x - 1) = (½) (x² - x)

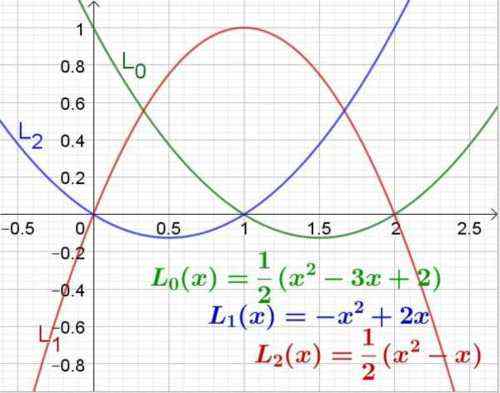Rajah 3. Polinomial LaGrange untuk Nilai Abscissa 0, 1 dan 2. Sumber: f. Zapata.

Contoh 2

Anda mahu menghampiri fungsi f (x) = arcan (x) Dalam selang waktu [0, 2]. Fungsi ini hanya nilai mereka diketahui x₀= 0, x₁= 1 dan x₂= 2, yang masing -masing dan₀= 0, dan₁= π/4 = 0.785 dan dan₂= 1,107.

Oleh itu anda perlu mencari polinomial interpoling P (x) menghampiri f (x) Dalam selang yang ditunjukkan.

Dalam Contoh 1, polinomial LaGrange telah ditentukan untuk nilai abscissa yang ditunjukkan dalam pernyataan ini, jadi tidak perlu mengulangi pengiraan. Interpoling Polynomial sekarang akan menjadi:

P (x) = f (x₀) L₀(x) + f (x₁) L₁(x) + f (x₂) L₂(x)

Yang bersamaan dengan:

P (x) = y₀ L₀(x) + dan₁ L₁(x) + dan₂ L₂(x)

Dalam kes ini, ia adalah:

P (x) = 0 ∙ (½) (x² - 3x + 2) + 0.785 ∙ (- x² + 2x) + 1,107 ∙ (½) (x² - x)

Perkara di atas dipermudahkan untuk:

P (x) = 0.785 ∙ (- x² + 2x) + 1,107 ∙ (½) (x² - x)

Dan akhirnya kekal:

P (x) = -0,2315 ∙ x² + 1,0165 ∙ x

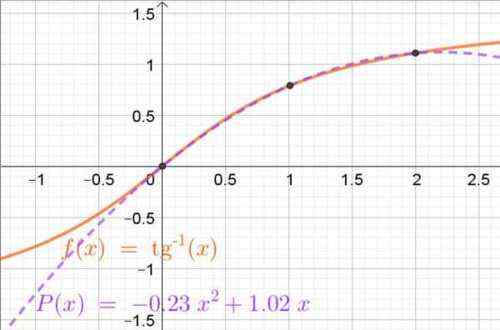Rajah 4. Interpoling Polynomial yang diperoleh melalui polinomial LaGrange yang menghampiri fungsi arka-tangen dalam selang (0, 2). Titik interpolasi juga ditunjukkan. Sumber: f. Zapata.

Latihan

Latihan 1

Dapatkan polinomial LaGrange yang mencukupi untuk mempunyai pendekatan untuk fungsi:

f (x) = dosa (x)

Dalam selang [0, π] dan dengan lima titik interpolasi.

Penyelesaian

Pada mulanya, abscissa titik interpolasi ditentukan, yang dipilih sama dan termasuk hujung selang penghampiran. Dengan ini anda mempunyai:

x₀= 0; x₁= π/4; x₂= π/2; x₃= 3 π/4; x₄= π.

Boleh melayani anda: Ketidaksamaan segitiga: demonstrasi, contoh, latihan yang diselesaikan

Oleh kerana f (x) dibatalkan pada titik yang melampau, tidak perlu untuk mendapatkan polinomial lagrange l l₀ dan l₄.

Polinomial l₁, L₂ dan l₃ adalah:

L₁ = [(x - x₀) / (X₁ - x₀)] [(x - x₂) / (X₁ - x₂)] [(x - x₃) / (X₁ - x₃)] [(x - x₄) / (X₁ - x₄)]

L₂ = [(x - x₀) / (X₂ - x₀)] [(x - x₁) / (X₂ - x₁)] [(x - x₃) / (X₂ - x₃)] [(x - x₄) / (X₂ - x₄)]

L₃ = [(x - x₀) / (X₃ - x₀)] [(x - x₁) / (X₃ - x₁)] [(x - x₂) / (X₃ - x₂)] [(x - x₄) / (X₃ - x₄)]

Sekarang kita menggantikan nilai abscissa:

L₁ = [(x - 0)/(π/4 - 0)] [(x - π/2)/(π/4 - π/2)] [(x - 3 π/4)/(π/4 - 3 π/4)] [(x - π)/(π/4 - π)]

L₂ = [(x - 0)/(π/2 - 0)] [(x - π/4)/(π/2 - π/4)] [(x - 3 π/4)/(π/2 - 3 π/4)] [(x - π)/(π/2 - π)]

L₃ = [(x - 0)/(3 π/4 - 0)] [(x - π/4)/(3 π/4 - π/4)] [(x - π/2)/(3 π/ 4 - π/2)] [(x - π)/(3 π/4 - π)]

Penyebut diselesaikan:

L₁ = [x/π/4] [(x - π/2)/( - π/4)] [(x - 3 π/4)/( - π/2)] [(x - π)/( - 3π/4)]

L₂ = [x/π/2] [(x - π/4)/(π/4)] [(x - 3 π/4)/( - π/4)] [(x - π)/( - π /2)]

L₃ = [x/(3 π/4)] [(x - π/4)/(π/2)] [(x - π/2)/(π/4)] [(x - π)/( - π/4)]

Ia dipermudahkan dan dikumpulkan semula untuk mendapatkan:

L₁ = x (x - π/2) (x - 3 π/4) (x - π)/( - 3 π ⁴/128)

L₂ = x (x - π/4) (x - 3 π/4) (x - π)/(π ⁴/64)

L₃ = x (x - π/4) (x - π/2) (x - π)/( - 3 π ⁴/128)

Latihan 2

Dapatkan polinomial interpolasi yang mendekati fungsi SEN (x) dalam selang [0, π] dengan lima titik interpolasi yang dipilih dalam Latihan 1 dan polinomial Lagrange masing -masing.

Penyelesaian

Polinomial interpolasi adalah:

P (x) = dosa (0) * l₀ + Sen (π/4) * l₁ + Sen (π/2) * l₂ + Sen (3π/4) * l₃ + Sen (π) * l4

Menilai fungsi sinus dan membiak adalah:

P (x) = (√2/2) l₁ + 1 * l₂ + (-√2/2) l₃

Selepas kerja algebra yang sukar, polinomial interpolasi adalah:

P (x) = 2. 7481 x⁴ -lima belas. 138 x³ +23. 467 x² - 9. 5236 x

Rujukan

1. Goodman, a. L. H. Sembilan belas sembilan puluh enam. Algebra dan trigonometri dengan geometri analisis. Pendidikan Pearson.
2. Harpe, ms. d. (2000). Topik dalam teori kumpulan geometri. Press University of Chicago.
3. Hazewinkel, m. (2001). Interpolasi linear ", Ensiklopedia Matematik.
4. Hoffmann, e. (2002). Ke kronologi interpolasi: dari astronomi kuno hingga isyarat moden dan pemprosesan imej. Prosiding IEEE.
5. Wikipedia. Interpolasi polinomial LaGrange. Pulih dari: wikipedia.com