Formula Ampère dan Undang -undang Persamaan, Demonstrasi, Latihan

The Undang -undang Ampère menyatakan bahawa peredaran vektor induksi magnet B Ia berkadar dengan intensiti dan arus yang mengalir dengan yang sama.

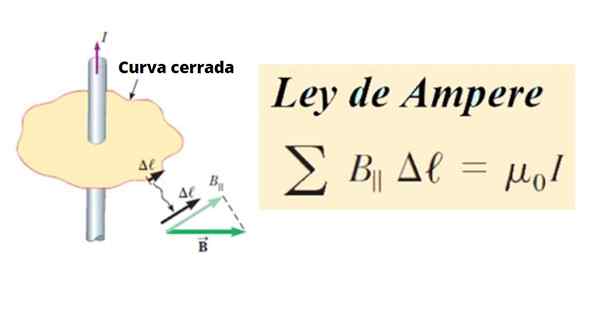
Seterusnya peredaran B Ia adalah jumlah semua produk antara komponen tangen b_║ dan panjang segmen kecil Δℓ lengkung tertutup c, Sekitar litar. Dalam istilah matematik ditulis seperti ini:

Σ b_║ .Δℓ ∝ Yo

Rajah 1. Definisi undang -undang ampere. Sumber: Serway, r. Fizik kolej.

Sebagai garis atau lengkung sewenang -wenangnya, ia boleh dibahagikan kepada segmen kecil Δℓ, Dan ini seterusnya boleh menjadi sangat kecil, maka mereka dipanggil dℓ.

Dalam kes ini, jumlahnya menjadi garis penting produk skalar antara vektor B dan ds. Produk ini mengandungi komponen tangen B, iaitu B cosθ, di mana θ adalah sudut antara vektor:

Lingkaran kecil yang melintasi integral bermakna integrasi dijalankan pada trajektori tertutup c, yang dalam kes ini melibatkan arus mengalir melalui bahagian silang pemandu.

Pemalar perkadaran yang diperlukan untuk mewujudkan kesamaan ialah μ_{Sama ada}, Kebolehtelapan vakum. Dengan cara ini, undang -undang Ampère kekal:

Undang -undang Ampère memberitahu kita bahawa garis integral ∫_C B ∙ ds Ia bernilai betul -betul μ_{Sama ada}Saya, tetapi ia tidak menawarkan kepada kita butiran tentang bagaimana medan magnet berorientasikan B Mengenai lengkung c pada setiap titik, atau bagaimana untuk mengira integral. Ia hanya memberitahu kita bahawa hasil yang sama selalu μ_{Sama ada}Yo.

[TOC]

Demonstrasi undang -undang Ampère

Undang -undang Ampère disahkan secara eksperimen memeriksa medan magnet yang dihasilkan oleh konduktor rectilinear yang sangat panjang. Sebelum menangani masalah ini, dua kes kepentingan khusus dalam persamaan sebelumnya mesti diserlahkan:

Ia dapat melayani anda: badan bercahaya: ciri -ciri dan bagaimana mereka menjana cahaya mereka sendiri

-Yang pertama adalah ketika B dan ds Mereka selari, yang bermaksud bahawa B adalah tangen untuk c. Kemudian sudut antara kedua -dua vektor adalah 0º dan produk skalar hanyalah produk magnitud B.ds.

-Yang kedua berlaku jika B dan ds Mereka berserenjang, di mana produk skalar adalah 0, kerana sudut antara vektor adalah 90º, yang kosininya adalah 0.

Satu lagi perincian penting ialah pilihan lengkung C di mana peredaran medan dinilai. Undang -undang Ampère tidak menentukan apa yang boleh, tetapi ia mesti membungkus taburan semasa. Juga tidak mengatakan bagaimana perjalanan lengkung dan terdapat dua kemungkinan untuk ini.

Penyelesaiannya adalah untuk memberikan tanda -tanda mengikut peraturan ibu jari yang betul. Empat jari melengkung ke arah yang anda ingin diintegrasikan, biasanya ini akan sama di lapangan B beredar. Sekiranya titik semasa ke arah ibu jari kanan, tanda diberikan dan jika tidak, tandatangan -.

Ini terpakai apabila terdapat pengedaran dengan beberapa arus, ada yang positif dan lain -lain negatif. Jumlah algebra mereka adalah apa yang akan kita letakkan dalam undang -undang Ampère, yang biasanya dilantik sebagai Arus yang tidak terperinci (Untuk lengkung c).

Medan magnet dawai rectilinear dan tak terhingga

Rajah 2 menunjukkan dawai yang mengangkut arus dan keluar dari pesawat. Peraturan ibu jari yang betul memastikan bahawa B Ia beredar ke arah yang bertentangan, menggambarkan lilitan seperti yang ditunjukkan oleh anak panah merah.

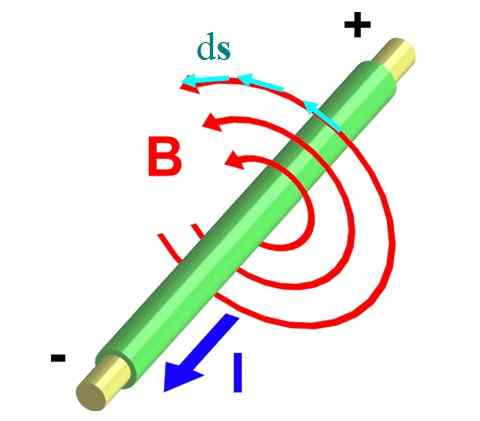Rajah 2.- Medan magnet dari dawai tak terhingga. Sumber: Wikimedia Commons.

Mari kita ambil salah satu daripada mereka, jejarinya adalah r. Kami membahagikannya ke segmen pembezaan kecil ds, diwakili dengan cara vektor biru. Kedua -dua vektor, B dan ds, Mereka selari pada setiap titik lilitan, dan dengan cara ini integral ∫_C B ∙ ds Ia berubah dalam:

Boleh melayani anda: Arus langsung

∫_C Bds

Ini kerana, seperti yang kita katakan sebelumnya, produk skalar B ∙ ds  Ia adalah produk magnitud vektor dengan kosinus 0º. Hasil dari integral diketahui terima kasih kepada undang -undang Ampère, oleh itu kita menulis:

∫_C Bds = μ_{Sama ada}Yo

Oleh kerana magnitud medan adalah malar ke atas keseluruhan trajektori, ia meninggalkan integral:

B ∫_C DS = μ_{Sama ada}Yo

Integral ∫_C DS mewakili jumlah semua segmen infinitesimal yang membentuk lilitan radio r, Bersamaan dengan panjangnya, produk radiusnya dengan 2π:

B.2πr = μ_{Sama ada}Yo

Dan dari sana kita mendapati bahawa magnitud b adalah:

B = μ_{Sama ada}I / 2πr

Adalah perlu untuk menekankan bahawa walaupun trajektori yang dipilih (atau litar amperian) Tidak bulat, hasil dari integral terus menjadi μ_{Sama ada}Saya, bagaimanapun ∫_C B ∙ ds Ia tidak lagi b.2πr.

Itulah sebabnya kegunaan undang -undang Ampère untuk menentukan medan magnet terletak pada memilih pengagihan dengan simetri yang tinggi, sehingga integral mudah dinilai. Lintasan pekeliling dan rectilinear memenuhi keperluan ini.

Latihan yang diselesaikan

- Latihan 1

Pertimbangkan lengkung a, b, c dan d ditunjukkan dalam Rajah 3. Mereka membungkus tiga arus, dua yang meninggalkan pesawat, dilambangkan dengan satu titik ( . ), intensitasnya adalah 1 a dan 5 a, dan arus yang memasuki pesawat, yang dilambangkan dengan salib dan magnitudnya adalah 2 a.

Cari arus yang dilampirkan oleh setiap lengkung.

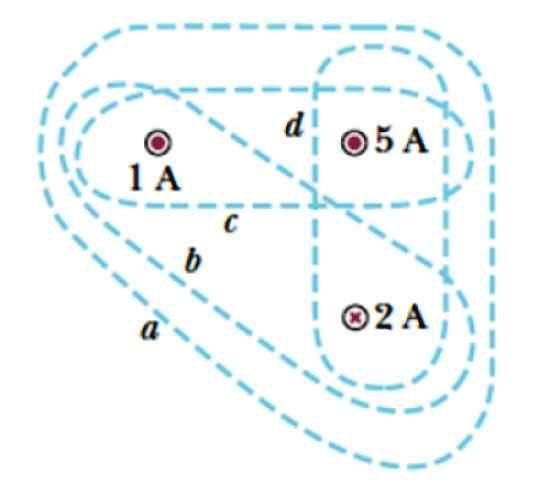Rajah 3. Beberapa lengkung untuk memohon undang -undang Ampère. Sumber: Serway, r. Fizik kolej.

Penyelesaian

Arus yang meninggalkan kertas diberikan tanda +. Menurut Ini:

Ia boleh melayani anda: gelombang cetek: ciri, jenis dan contoh

Lengkung a

Melampirkan tiga arus, oleh itu arus tertutup ialah + 1 a + 5 a - 2 a = 4 a.

Lengkung b

Hanya arus 1 a y - 2 a berada di dalam lengkung ini, oleh itu arus tertutup adalah dari - 2 a.

Lengkung c

Mengandungi arus keluar 1 dan 5 a, oleh itu arus tertutup ialah 6 a.

Lengkung d

Arus di dalamnya adalah +5 a dan - 2 a, kemudian melampirkan arus bersih 3 hingga.

- Latihan 2

Kirakan magnitud medan magnet yang dihasilkan oleh dawai rectilinear yang sangat panjang.

Penyelesaian

Menurut undang -undang Ampère, medan wayar diberikan oleh:

B = μ_{Sama ada}I / 2πr = (4π x 10^-7 x 1/2π x 1) t = 2 x 10^-7 T.

Rujukan

1. Figueroa, d. (2005). Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 6. Elektromagnetisme. Diedit oleh Douglas Figueroa (USB).
2. Knight, r.  2017. Fizik untuk saintis dan kejuruteraan: Pendekatan Strategi.  Pearson.
3. Sears, Zemansky. 2016. Fizik universiti dengan fizik moden. Ke -14. Ed. Jilid 2.
4. Serway, r. 2009. Fizik kolej. Pembelajaran Cengage.
5. Tipler, ms. (2006) Fizik untuk Sains dan Teknologi. Edisi ke -5. Jilid 2. Editorial kembali.