Formula Undang -undang Hooke, Contoh, Aplikasi, Latihan

The Undang -undang Hooke menunjukkan bahawa ubah bentuk yang dialami oleh objek elastik berkadar terus dengan daya yang digunakan di atasnya. Pemalar perkadaran bergantung pada sifat objek, geometrinya dan bahan yang dihasilkannya.

Semua bahan mempunyai sifat elastik ke tahap yang lebih besar atau lebih rendah, sehingga mereka mematuhi undang -undang Hooke setiap kali mereka kembali ke dimensi asal mereka, setelah kekuatan berhenti. Mata air elastik dan gusi adalah contoh objek yang baik yang mematuhi undang -undang Hooke, tetapi begitu juga cabilla keluli yang merupakan sebahagian daripada jambatan.

Rajah 1. Undang -undang Hooke pada musim bunga

Mengambil sebagai contoh musim bunga atau dok, untuk memastikan ia diregangkan atau dimampatkan, adalah perlu untuk memohon daya yang magnitudnya adalah f. Menurut undang -undang Hooke, musim bunga akan mengalami ubah bentuk X:

F ∝ x

Pemalar perkadaran, yang, sebagai musim bunga, dipanggil kekakuan musim bunga, Ia dilambangkan sebagai k, oleh itu:

F = k ⋅x

Di unit sistem antarabangsa, daya datang di Newton (n) dan ubah bentuk dalam meter (m). Oleh itu, pemalar musim bunga mempunyai unit N/M. Pemalar musim bunga mewakili daya yang mesti digunakan untuk mengubahnya dalam panjang 1 m.

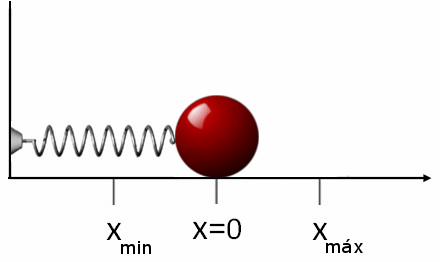Rajah 2. Apabila musim bunga diregangkan, daya yang dikenakan ke atas objek itu bertentangan. Perkara yang sama berlaku jika musim bunga mengecut, dalam hal ini ia memacu objek dalam erti kata yang bertentangan. Sumber: Wikimedia Commons.

Sekiranya selepas meregangkan atau memampatkan musim bunga, ia akan dibebaskan, ia akan bergerak ke arah yang bertentangan dengan daya yang digunakan. Ini bermaksud bahawa jika kita meregangkannya, ia dimampatkan dan sebaliknya. Itulah sebabnya daya f_R itu Latihan musim bunga adalah:

F_R = -K ⋅x

Tanda negatif menunjukkan apa yang dikatakan: bahawa daya menentang anjakan, jadi kekuatan ini dikenali sebagai Daya pemulihan.

[TOC]

Formula dan persamaan

Hubungan antara daya dan pemindahan pada musim bunga ditemui oleh Robert Hooke (1635-1703), seorang ahli fizik Inggeris yang terkenal dan terkenal dengan persaingan dengan Isaac Newton. Hooke adalah seorang saintis serba boleh yang berjaya dalam bidang sains yang berbeza: mekanik, biologi, astronomi dan seni bina.

Rajah 3. Ahli fizik Inggeris Robert Hooke, yang tidak tahu potret masa itu. Ini adalah pembinaan semula yang dibuat oleh artis Rita Gerer pada tahun 2004 melalui deskripsi yang ditinggalkan oleh mereka yang bertemu dengan saintis. Sumber: Wikimedia Commons. Rita Greer / Fal.

Hooke menyedari bahawa jika daya yang digunakan untuk dermaga tidak begitu besar, dok adalah deformasi yang berkadar untuk memaksa, dan pernah berkata daya hilang, musim bunga mempunyai panjang semula jadi lagi.

Boleh melayani anda: magnetosfera bumi: ciri, struktur, gas

Dengan cara ini, undang -undang Hooke secara grafik mempunyai bentuk garis lurus, yang cerunnya adalah pemalar musim bunga. Imej berikut menunjukkan daya yang dikenakan pada musim bunga untuk meregangkannya - atau memampatkannya - bergantung pada kedudukan x. Perhatikan bahawa daya tidak bergantung pada panjang semulajadi musim bunga, tetapi pada anjakannya.

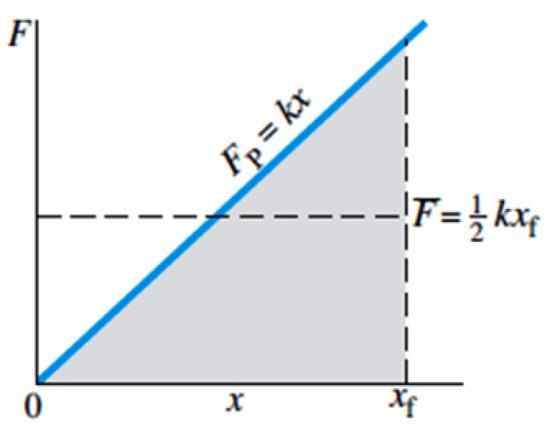Rajah 4. Magnitud F dari daya yang diperlukan untuk meregangkan atau memampatkan musim bunga, bergantung kepada ubah bentuk x. Sumber: Giancoli, D. Fizik dengan aplikasi.

Daya purata ditunjukkan dalam graf oleh f dengan bar dan bersamaan dengan ½ kx_F, di mana x_F adalah kedudukan akhir musim bunga.

Kedua -dua kekuatan yang dikenakan pada musim bunga, dan kekuatan yang dia lakukan pada objek yang terikat kepadanya, adalah pasukan yang berubah -ubah. Semakin banyak anda ingin meregangkan atau memampatkan pada musim bunga, semakin banyak kekuatan yang anda perlukan untuk dapat mencapainya.

Kerja yang dilakukan untuk meregangkan atau memampatkan musim bunga

Apabila daya digunakan yang mengubah bentuk musim bunga, kerja yang disimpan pada musim bunga dilakukan dan boleh digunakan kemudian.

Kerja mekanikal ditakrifkan sebagai kawasan di bawah graf daya F bergantung pada kedudukan x. Untuk mengira kerja w yang menjadi daya berubah f (x) membuat ketika memindahkan objek dari kedudukan x₁ untuk meletakkan x₂ Integral yang ditakrifkan mesti dikira:

Dalam kes kerja yang diperlukan untuk membawa musim bunga dari kedudukan keseimbangannya untuk kedudukan x_F Ia sangat mudah, kerana kawasan yang akan dikira adalah segitiga teduh kelabu Rajah 4, yang formulanya diketahui:

Kawasan segitiga = ½ asas. ketinggian

Oleh itu kerja yang diperlukan adalah:

W = ½ x_F . (Kx_F) = ½ k (x_F)²

Dan jika anda ingin mengira kerja yang diperlukan untuk dibawa ke musim bunga dari kedudukan x ke kedudukan x_F, Ia bersamaan dengan mengira kawasan trapeze tercalar dalam Rajah 5:

W = ½ k (x_F)² - ½ k x²

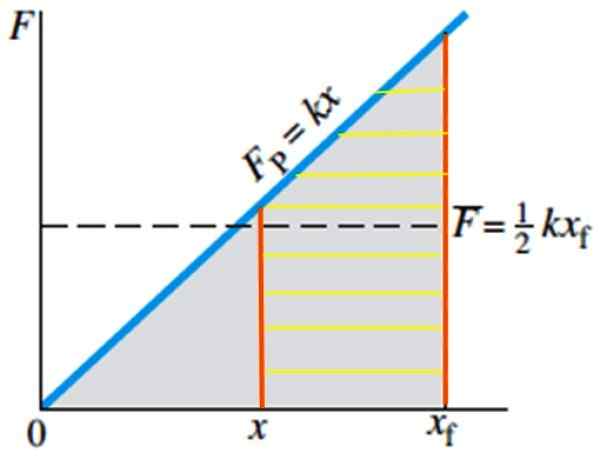Rajah 5. Kerja yang dilakukan untuk meregangkan musim bunga dari kedudukan x ke kedudukan XF bersamaan dengan kawasan Rayada. Sumber: Giancoli, D. Fizik dengan aplikasi.

Contoh mata air

Menurut permohonan yang dimaksudkan, mata air boleh menjadi silinder, kerucut, lingkaran, dengan seksyen salib bulat (yang paling biasa), seksyen persegi atau segi empat tepat.

Boleh melayani anda: konduktor elektrik

Klasifikasi yang digunakan secara meluas adalah mengikut jenis usaha yang mereka akan tertakluk: terdapat kilasan, fleksi, mampatan dan lanjutan mata air. Yang terakhir digunakan secara meluas dan ada juga yang berfungsi untuk ketegangan dan pemampatan.

Spring mampatan

Contoh musim bunga mampatan adalah apa yang digunakan dalam mainan yang dipanggil Pogo Sama ada Saltoín Palo. Mata air ini menyimpan tenaga yang berpotensi apabila dimampatkan dan dibebaskan secara beransur -ansur semasa kembali ke kedudukan keseimbangan. Dengan cara ini rebound tidak terlalu tiba -tiba.

Rajah 6. Tongkat pogo atau saltoín berdasarkan musim bunga mampatan. Sumber: Wikimedia Commons.

Lanjutan dan mata air kilasan

Musim bunga untuk spramp adalah jenis mata air lanjutan dan dihasilkan dengan giliran yang baik, dengan dua cangkuk di hujungnya. Mereka dapat mengekalkan tenaga berpotensi yang cukup, yang kemudiannya dibebaskan ketika seseorang bangkit dan mula melompat pada kanvas, yang juga mempunyai tindak balas elastik mereka sendiri, seperti semua bahan.

Mata air kilasan sangat biasa, kerana mereka berkhidmat untuk membuat pengapit pakaian. Daripada cangkuk di hujungnya, mereka membungkuk pada sudut, untuk menahan daya yang cenderung untuk menjalankan kilasan.

Rajah 7. Mata air adalah sebahagian daripada mekanisme yang tidak terhitung jumlahnya, seperti pinset pakaian ini. Sumber: Pxfuel.

Bahan untuk pembuatan mata air

Bahan yang paling sesuai untuk menjadikan mata air adalah mereka yang mempunyai Rintangan muktamad (Rintangan Akhir), iaitu, mereka menyokong usaha yang hebat sebelum melanggar. Ia juga mudah bahawa bahan mempunyai titik rayap yang tinggi, sehingga tidak kehilangan kualiti elastiknya dengan usaha kecil.

Mata air penggunaan perindustrian dihasilkan dengan aloi yang termasuk keluli dengan kandungan karbon, tembaga, nikel dan gangsa yang tinggi.

Permohonan Undang -undang Hooke

Memandangkan mata air mempunyai kebaikan menyimpan tenaga yang berpotensi apabila mereka meregangkan atau memampatkan, mereka dapat melakukan kerja dengan menggerakkan perkara seperti mekanisme.

Dengan cara ini mata air mempunyai banyak aplikasi, dari objek kecil dan harian, melalui kereta, ke jentera dari semua jenis. Mata air berfungsi untuk:

-Getaran kejutan.

-Mekanisme yang boleh ditarik balik: Pen, Pineezers Gantung, Cangkuk Rambut.

-Buat musim bunga atau dinamometer

Dan mereka juga merupakan sebahagian daripada mekanisme:

Boleh melayani anda: litar elektrik tertutup

-Jam tangan.

-Trampolin.

-Kunci.

-Mainan.

-Senjata.

-Meter jarum, contohnya galvanometer, digunakan untuk mengukur arus, voltan dan rintangan.

Latihan yang diselesaikan

- Latihan 1

Kekuatan magnitud 5 digunakan.0 N pada musim bunga, membuat panjang 3 regangan.5 cm dari panjang semula jadi.

a) berapa banyak yang diregangkan apabila daya yang digunakan adalah 7 n?

b) Cari kerja yang dilakukan oleh daya yang digunakan untuk meregangkan ke musim bunga 3.5 cm dari panjang semula jadi.

Penyelesaian kepada

Mengetahui bahawa musim bunga adalah regangan 3.5 cm melalui permohonan 5.0 N Kami boleh mengira pemalar anda:

k = f / x = 5.0 n / 3.5 cm = 1.43 n / cm.

Apabila daya 7 N digunakan, peregangan berikut diperoleh:

x = f / k = 7.0 n / 1.43 n/m = 4.9 cm

Penyelesaian b

Kerja yang diperlukan untuk mengubah bentuk musim bunga diberikan oleh:

W = ½ kx² = 0.5 x 1.43 n / cm x (3.5 cm)² = 8.76 n . CM = 8.76 n . 1 x10 ^-2 m = 0.0876 J.

- Latihan 2

Musim bunga adunan yang hina dan 10 cm panjang tergantung dari sokongan. Sekiranya jisim 2 kg digantung, musim bunga diregangkan sehingga mencapai 15 cm. Kira:

a) pemalar musim bunga

b) saiz musim bunga apabila jisim 3 kg digantung.

Penyelesaian kepada

Peregangan musim bunga adalah x = 15 - 10 cm = 5 cm

Oleh kerana sistem berada dalam keseimbangan statik, daya yang dikenakan oleh musim bunga apabila peregangan diarahkan secara menegak ke atas, untuk mengimbangi berat badan, yang diarahkan, kemudian:

F_R = W → kx = mg

K = 2 x 9.8 n / 5 x10 ^-2 M = 392 n/m

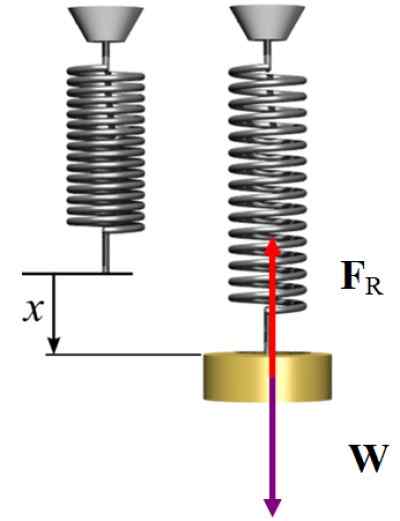Rajah badan percuma untuk latihan diselesaikan 2. Sumber: Wikimedia Commons/F. Zapata.

Penyelesaian b

Apabila berat 3 kg digantung, daya baru adalah w = 3 x 9.8 n = 29.4 n

Dalam kes ini, peregangannya adalah:

x = mg /k = 29. 4 N / 392 N / M = 0.075 m = 7.5 cm

Rujukan

1. Bauer, w. 2011. Fizik untuk Kejuruteraan dan Sains. Jilid 1. MC Graw Hill.
2. Blog Mekanisme Kreatif. Empat jenis mata air. Pulih dari: creativememechanisms.com.
3. Figueroa, d. (2005). Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 2. Dinamik. Diedit oleh Douglas Figueroa (USB).
4. Giancoli, d.  2006. Fizik: Prinsip dengan aplikasi. 6th. Ed. Prentice Hall.
5. Knight, r.  2017. Fizik untuk saintis dan kejuruteraan: Pendekatan Strategi.  Pearson.