Penjelasan Undang -undang Kepler, Latihan, Eksperimen

The Undang -undang Kepler Mengenai pergerakan planet ini dirumuskan oleh ahli astronomi Jerman Johannes Kepler (1571-1630). Kepler menyimpulkan mereka berdasarkan karya guru Denmark Gurunya Tycho Brahe (1546-1601).

Brahe dengan teliti menyusun data dari pergerakan planet lebih dari 20 tahun, dengan ketepatan dan ketepatan yang mengejutkan, jika diambil kira bahawa pada masa teleskop belum dicipta. Kesahan data anda masih sah hari ini.

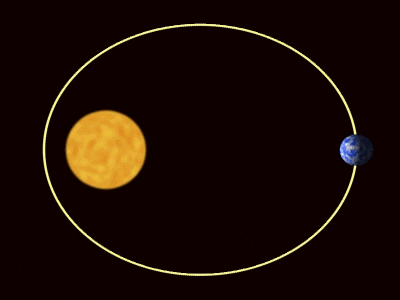Rajah 1. Orbit planet mengikut undang -undang Kepler. Sumber: Wikimedia Commons. Willow/CC oleh (https: // creativeCommons.Org/lesen/oleh/3.0)

[TOC]

3 undang -undang Kepler

Undang -undang Kepler menubuhkan:

-Undang -undang Pertama: Semua planet menggambarkan orbit elips dengan matahari di salah satu lampu sorot.

-Undang -undang kedua atau undang -undang yang sama: Garis yang diarahkan dari matahari ke mana -mana planet (radio fokus), menyapu kawasan yang sama dengan masa yang sama.

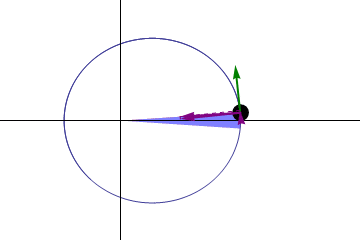Rajah 2. Undang -undang kawasan. Sumber: Wikimedia Commons. Gonfer/CC BY-SA (https: // creativeCommons.Org/lesen/by-sa/3.0)

-Undang -undang Ketiga: Dataran masa yang mengambil mana -mana planet orbital di sekitar matahari adalah berkadar dengan kiub jarak rata -rata ke matahari.

Menjadi T berkata masa, dipanggil Tempoh orbit, dan r Jarak purata, kemudian:

T² berkadar dengan r³

T = k r³

Ini bermaksud bahawa kota T²/ r³ Ia adalah sama untuk semua planet, yang memungkinkan untuk mengira jejari orbital, jika tempoh orbital diketahui.

Bila T Ia dinyatakan dalam tahun dan r Dalam unit astronomi ua*, pemalar perkadaran bernilai k = 1:

T²= r³

*Unit astronomi bersamaan dengan 150 juta kilometer, yang merupakan jarak purata antara bumi dan matahari. Tempoh orbital bumi adalah 1 tahun.

Undang -undang Gravitasi Sejagat dan Undang -undang Ketiga Kepler

Undang -undang graviti sejagat menetapkan bahawa magnitud daya tarikan graviti antara dua objek massa M dan m masing -masing, pusatnya berasingan jauh r, Ia diberikan oleh:

F = g mm /r²

G adalah pemalar graviti sejagat dan nilainya adalah g = 6.674 x 10 ^-sebelas N.m²/kg² .

Sekarang, orbit planet adalah elips dengan eksentrik yang sangat kecil.

Ini bermakna orbit tidak bergerak jauh dari bulatan, kecuali dalam beberapa kes seperti Pluto kerdil. Jika kita menghampiri orbit ke bentuk bulat, percepatan pergerakan planet adalah:

ke_c = v²/r

Diberi F = ma, mempunyai:

G mm /r² = m.v²/r

Di sini v Ini adalah kelajuan linear planet di sekeliling matahari, statik dan massa M, Walaupun planet ini m. Jadi:

Boleh melayani anda: Angka penting: peraturan, contoh, latihan yang diselesaikan

Ini menjelaskan bahawa planet paling jauh dari matahari mempunyai kelajuan orbital yang lebih rendah, kerana ia bergantung pada 1/√r.

Oleh kerana jarak planet ini adalah kira -kira panjang lilitan: l = 2πr dan ia mengambil masa yang sama t, tempoh orbit, ia diperolehi:

V = 2πr /t

Menyamakan kedua -dua ungkapan untuk v ungkapan yang sah untuk t diperolehi², Dataran tempoh orbit:

Dan ini adalah undang -undang ketiga Kepler yang tepat, kerana dalam ungkapan ini kurungan 4π² /Gm Oleh itu, ia tetap T² berkadar dengan jarak r ditinggikan ke kiub.

Persamaan muktamad untuk tempoh orbital diperolehi dengan mengekstrak akar persegi:

Mengira jisim matahari

Berapa jisim matahari? Adalah mungkin untuk mengetahui melalui persamaan ini. Kami tahu bahawa tempoh orbital bumi adalah satu tahun dan radius orbital adalah 1 ua, bersamaan dengan 150 juta kilometer, jadi kami mempunyai semua data yang diperlukan.

Dalam persamaan kami sebelum ini, kami membersihkan M, Tetapi tidak sebelum menukar semua nilai ke sistem unit antarabangsa jika:

1 tahun = 3.16 x 10⁷ saat.

1 ua = 150 juta km = 1.5 x10^sebelas m.

Dan dengan menggantikan data dalam persamaan, kami memperoleh anggaran yang cukup berjaya matahari matahari dalam 2.0 x 10 ³⁰ kg.

Latihan

Walaupun Kepler hanya mempunyai planet -planet dalam fikiran ketika dia memperoleh undang -undang terkenalnya, ini juga sah untuk pergerakan satelit dan badan -badan lain sistem suria, seperti yang akan kita lihat seterusnya.

- Latihan 1

Mengetahui bahawa orbit Musytari adalah 5.19 kali lebih besar daripada bumi, cari tempoh orbit Musytari.

Penyelesaian

Menurut definisi unit astronomi, Musytari adalah dari matahari 5.19 UA, oleh itu, menurut Undang -undang Ketiga Kepler:

T²= r³= (5.19)³ tahun

Oleh itu T = (5.19)^3/2  tahun = 11.8 tahun

- Latihan 2

Halley Comet melawat matahari setiap 75.3 tahun. Cari:

a) separuh hearing orbitnya.

b) ukuran apelium, jika perihelium mengukur 0.568 ua.

Penyelesaian

Halley Comet melawat matahari setiap 75.3 tahun. Cari:

a) separuh hearing orbitnya.

b) ukuran apelium, jika perihelium mengukur 0.568 ua.

Penyelesaian kepada

Apabila planet atau bintang lain berada pada titik paling dekat dengan matahari, dikatakan bahawa ia berada di perihelio, Dan apabila lebih jauh, masuk Aphelion. Dalam kes khas orbit bulat, r dalam undang -undang ketiga Kepler adalah jejari orbit.

Boleh melayani anda: pemalar antoin: formula, persamaan, contoh

Walau bagaimanapun, dalam orbit elips, badan angkasa lebih kurang dari matahari, sebagai separuh "a" purata antara aprotess dan perihelium:

Rajah 3. Aflio dan Perihelio. Sumber: Wikimedia Commons. Pearson Scott Foresman / Domain Awam

Oleh itu, kita menggantikan R oleh A dalam undang -undang ketiga Kepler, yang menghasilkan Halley dalam:

T²= a³→ A = (t)²³ → A = (75.3) ²³ Ua = 17.832 ua

Penyelesaian b

A = ½ (Perihelio + Apelio)

17.832 = ½ (0.568+ aflio) → Aflio = 2 x 17.832 - 0.568 ua = 35.10 ua.

Eksperimen

Menganalisis pergerakan planet memerlukan minggu, bulan dan bahkan bertahun -tahun pemerhatian dan pendaftaran yang teliti. Tetapi di makmal percubaan yang sangat mudah dapat dijalankan untuk membuktikan bahawa undang -undang Kepler bersamaan dipenuhi.

Untuk ini, sistem fizikal diperlukan di mana daya yang mengawal pergerakan itu adalah keadaan yang sentral, yang mencukupi bagi undang -undang kawasan yang akan dipenuhi. Sistem sedemikian terdiri daripada jisim yang terikat dengan tali yang panjang, dengan ujung benang tetap yang lain ke sokongan.

Doh memisahkan sudut kecil kedudukan keseimbangannya dan dicetak sedikit dorongan, sehingga ia melaksanakan gerakan bujur (hampir elips) pada satah mendatar, seolah -olah ia adalah planet di sekitar matahari.

Pada lengkung yang diterangkan oleh pendulum, kita dapat membuktikan bahawa ia menyapu kawasan yang sama dalam masa yang sama, ya:

-Kami menganggap radio vektor dari pusat tarikan (titik keseimbangan awal) ke kedudukan jisim.

-Dan kita barmos antara dua momen berturut -turut yang sama, dalam dua bidang pergerakan yang berbeza.

Semakin lama benang pendulum dan semakin rendah sudut yang berlepas dari menegak, daya pemulihan bersih akan lebih mendatar dan simulasi menyerupai kes pergerakan dengan daya pusat dalam satah.

Kemudian bujur yang diterangkan mendekati elips, seperti yang dilakukan oleh planet.

Bahan

-Benang yang tidak dapat dipertahankan

-1 doh atau bola logam dicat putih yang bertindak sebagai pendulum lentil

-Pembaris

-Penghantar

-Kamera gambar dengan cakera strob automatik

-Menyokong

-Dua sumber pencahayaan

-Sekeping kertas atau kadbod hitam

Ia dapat melayani anda: Teori Big Crunch: Sejarah, Prinsip, Data untuk dan Terhadap

Prosedur

Perhimpunan angka diperlukan untuk mengambil gambar pelbagai kilat pendulum sebagai trajektorinya diikuti. Untuk melakukan ini, anda perlu meletakkan kamera tepat di atas pendulum dan album strob automatik di hadapan lensa.

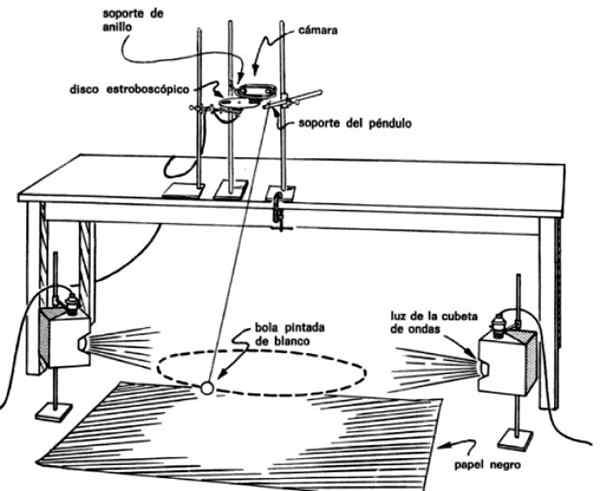Rajah 4. Pemasangan pendulum untuk mengesahkan bahawa ia menyapu kawasan yang sama dengan masa yang sama. Sumber: Panduan Makmal PSSC.

Dengan cara ini, imej diperoleh pada selang masa pendulum, contohnya setiap 0.1 atau setiap 0.2 saat, yang membolehkan mengetahui masa yang diperlukan untuk bergerak dari satu titik ke yang lain.

Anda juga perlu menerangi jisim pendulum dengan mudah, meletakkan lampu di kedua -dua belah pihak. Lentil mesti dicat putih untuk memperbaiki kontras di latar belakang, yang terdiri daripada kertas hitam yang dilanjutkan di tanah.

Sekarang anda harus memeriksa bahawa pendulum menyapu kawasan yang sama dengan masa yang sama. Untuk ini, selang masa dipilih dan mata yang diduduki oleh pendulum dalam selang tersebut ditandakan di atas kertas.

Pada imej garis diambil dari pusat bujur ke titik -titik ini dan oleh itu kita akan mempunyai yang pertama di kawasan yang disapu oleh pendulum, yang kira -kira sektor elips seperti yang ditunjukkan di bawah:

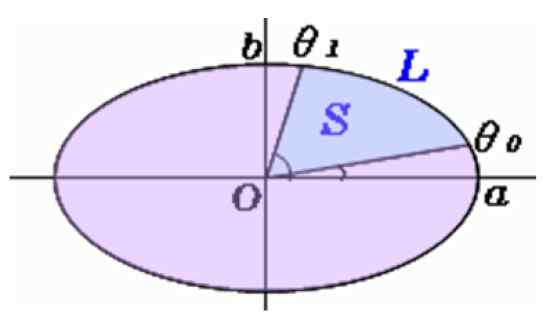Rajah 5. Kawasan sektor elips. Sumber: f. Zapata.

Pengiraan kawasan seksyen elips

Sudut diukur dengan penghantar θ_{Sama ada} dan θ₁, Dan formula ini digunakan untuk mencari s, kawasan sektor elips:

S = f (θ₁) - f (θ_{Sama ada})

Dengan F (θ) diberikan oleh:

Perhatikan bahawa ke dan b Mereka adalah separuh -senijes yang lebih besar dan kecil masing -masing. Pembaca hanya perlu berhati -hati untuk mengukur dengan teliti separuh dan sudut, kerana terdapat kalkulator dalam talian untuk menilai ungkapan ini dengan mudah.

Walau bagaimanapun, jika anda mendesak untuk membuat pengiraan dengan tangan, anda harus ingat bahawa sudut θ diukur dalam darjah, tetapi pada masa memasuki data ke kalkulator, nilai -nilai mesti dinyatakan dalam radianes.

Kemudian anda perlu menandakan satu lagi mata di mana pendulum telah melabur selang masa yang sama, dan melukis kawasan yang sepadan, mengira nilainya dengan prosedur yang sama.

Pengesahan undang -undang kawasan yang sama

Akhirnya ia tetap untuk mengesahkan bahawa undang -undang kawasan dipenuhi, iaitu, pada masa yang sama kawasan yang sama menyapu.

Adakah hasilnya menyimpang sedikit dari apa yang diharapkan? Anda harus ingat bahawa semua langkah disertai dengan kesilapan eksperimen masing -masing.

Rujukan

1. Kalkulator Online Keisan. Kawasan kalkulator sektor elips. Pulih dari: Keisan.Casio.com.
2. Opentax. Undang -Undang Pergerakan Planet Keepler. Diperolehi dari: OpenStax.org.
3. PSSC. Fizik Makmal. Editorial kembali. Pulih dari: buku.Google.co.
4. Palen, s. 2002. Astronomi. Siri Schaum. McGraw Hill.
5. Pérez r. Sistem Mudah Dengan Kekuatan Pusat. Pulih dari: Francesphysics.Blogspot.com
6. Stern, d. Ketiga Undang -undang Kepler Pergerakan Planet. Pulih dari: phy6.org.