Undang -undang Kirchhoff

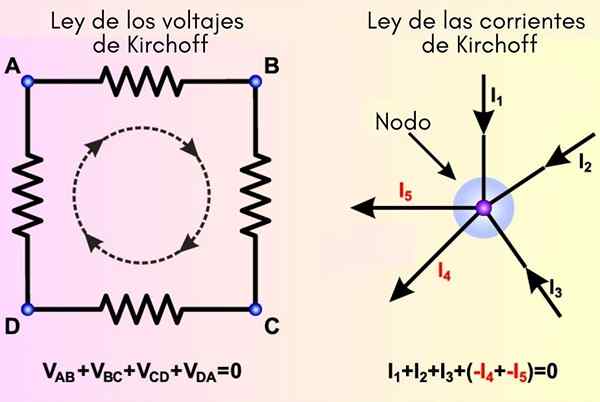
Undang -undang Kirchoff berasal dari prinsip -prinsip tenaga dan pemuliharaan beban. Di sebelah kiri, undang -undang jejaring ditubuhkan dan di sebelah kanan arus

Apakah undang -undang Kirchoff?

The Undang -undang Kirchoff Mereka terdiri daripada menerapkan prinsip pemuliharaan caj elektrik dan prinsip pemuliharaan tenaga ke litar elektrik, untuk menyelesaikannya yang mempunyai beberapa jejaring.

Peraturan ini, kerana mereka bukan undang-undang dalam erti kata yang ketat, adalah disebabkan oleh ahli fizik Jerman Gustav Kirchoff (1824-1887). Penggunaannya adalah penting apabila undang -undang Ohm tidak mencukupi untuk menentukan voltan dan arus di litar.

Sebelum pernyataan dan permohonan undang -undang Kirchoff, adalah mudah untuk mengingati makna beberapa konsep penting mengenai litar elektrik:

• Nod: Titik kesatuan antara dua atau lebih wayar konduktif.
• Cawangan: Unsur -unsur litar yang antara dua nod berturut -turut, di mana arus yang sama beredar.
• Mesh: gelung trajektori atau tertutup terdiri daripada dua atau lebih cawangan dan yang berjalan ke arah yang sama, tanpa melalui titik yang sama.

Undang -undang pertama Kirchoff

Ia juga dikenali sebagai undang -undang arus atau peraturan nod, dan menetapkan bahawa:

Jumlah arus yang memasuki nod adalah sama dengan jumlah arus yang keluar daripadanya.

Jadi, dengan cara matematik, undang -undang pertama dinyatakan sebagai:

Σ i = 0

Di mana simbol σ menunjukkan jumlah.

Persamaan sebelumnya menetapkan bahawa, kerana caj elektrik tidak dibuat atau dimusnahkan, keseluruhan arus (beban per unit masa) yang memasuki nod mestilah sama dengan yang keluar dari situ.

Boleh melayani anda: satelit buatan

Contoh

Untuk memohon undang -undang arus, tanda diberikan kepada arus masuk, dan tanda bertentangan dengan arus keluar. Pilihannya benar -benar sewenang -wenang.

Imej berikut menunjukkan dua arus yang memasuki nod, ditarik merah: i₁ dan saya₂, dan ketika meninggalkan mereka ditunjukkan dalam warna hijau: arus i₃, Yo₄ dan saya₅.

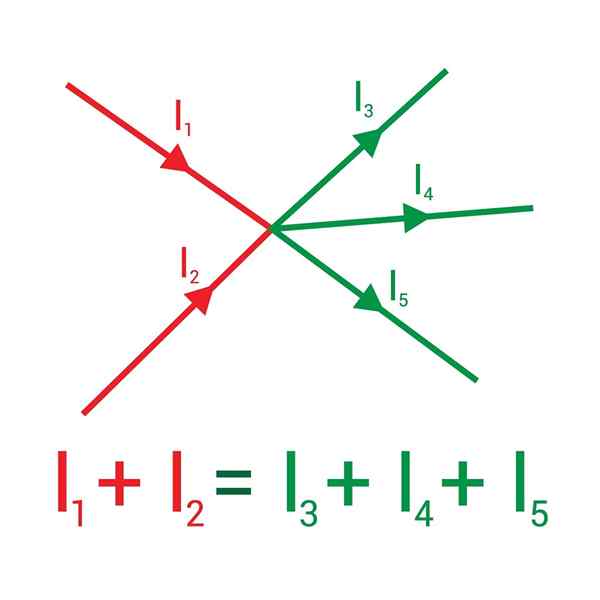Jumlah arus yang memasuki nod sama dengan jumlah arus yang keluar daripadanya

Menetapkan tanda (+) kepada arus masuk, dan (-) kepada yang keluar, peraturan pertama Kirchoff menetapkan bahawa:

Yo₁ + Yo₂ - Yo₃ - Yo₄ - Yo₅= 0 ⇒ i₁ + Yo₂ = I₃ + Yo₄ + Yo₅

Undang -undang kedua Kirchoff

Nama lain untuk undang -undang kedua Kirchoff adalah: Undang -undang Voltan, Undang -undang Ketegangan Sama ada Undang -undang mesh. Walau apa pun, ia menetapkan bahawa:

Jumlah voltan algebra yang jatuh di sepanjang mesh adalah sama dengan 0.

Ini adalah cara untuk menggunakan pemuliharaan tenaga dalam litar, kerana voltan dalam setiap elemen adalah perubahan tenaga per unit beban.

Oleh itu, ketika mengembara bahagian tertutup (mesh), jumlah algebra peningkatan voltan dan jatuh adalah 0 dan boleh ditulis:

Σ v = 0

Contoh

Dalam angka berikut, anda mempunyai mesh Abcda, di mana arus beredar ke arah jarum jam dan laluan boleh bermula pada bila -bila masa di litar.

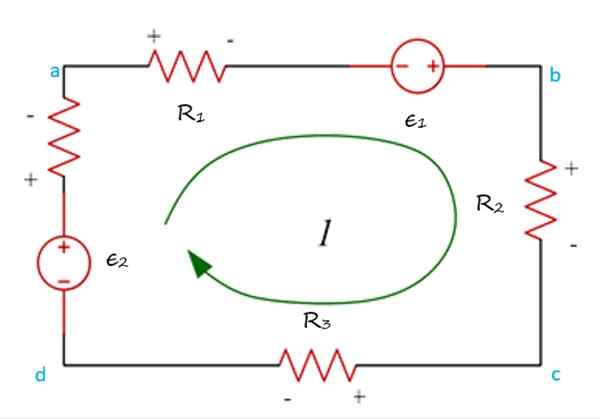Contoh mesh yang dilawati dalam jadual, di mana kenaikan dan potensi jatuh ditunjukkan untuk memohon undang -undang ketegangan kirchoff. Sumber: f. Zapata.

Ia juga perlu. Yang biasa adalah untuk memberikan positif voltan kenaikan, iaitu, apabila arus beredar dari ( -) ke (+). Kemudian, penurunan ketegangan, yang berlaku apabila arus pergi dari (+) ke ( -), adalah negatif.

Boleh melayani anda: silikon oksida (SiO2): struktur, sifat, kegunaan, memperoleh

Memulakan laluan mesh pada titik "a", adalah rintangan r₁. Di dalamnya, beban mengalami penurunan yang berpotensi, dilambangkan oleh tanda -tanda (+) di sebelah kiri dan ( -) di atas rintangan.

Oleh itu, voltan atau voltan dalam r₁ Ia mempunyai tanda negatif.

Kemudian anda mencapai sumber voltan langsung, yang dipanggil ε₁, yang polaritasnya kurang (-) Lebih banyak (+). Di sana caj elektrik melalui potensi kenaikan dan sumber ini dianggap sebagai positif.

Berikutan prosedur ini untuk rintangan yang tinggal dan sumber lain, persamaan berikut diperolehi sebagai hasilnya:

-V₁ + ε₁ - V₂ - V₃ + ε₂ = 0

Di mana v₁, V₂ dan v₃ Adakah ketegangan dalam rintangan r₁, R₂ dan r₃. Ketegangan ini boleh didapati dari undang -undang ohm: v = i · r.

Latihan diselesaikan

Cari nilai arus i₁, Yo₂ dan saya₃ ditunjukkan dalam angka.

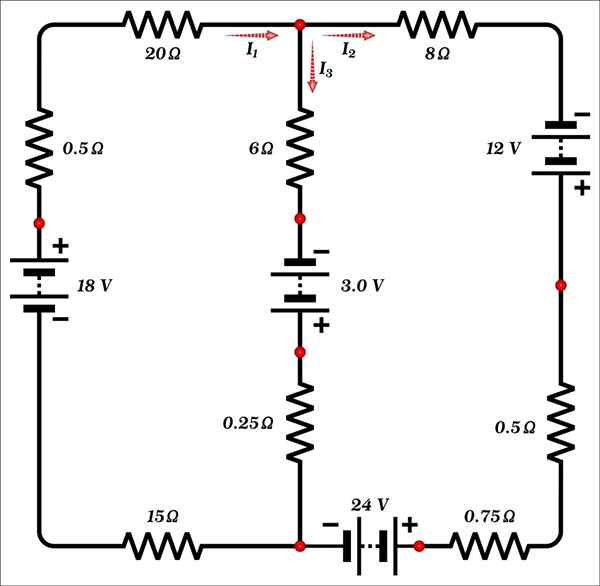
Penyelesaian

Litar ini hanya terdiri daripada dua jejaring dan mempunyai 3 orang yang tidak diketahui: arus dan₁, Yo₂ dan saya₃, Jadi sekurang -kurangnya 3 persamaan diperlukan untuk mencari penyelesaiannya.

Di dalam nod (titik ditandakan dengan merah) yang berada di bahagian atas litar di cawangan pusat, diperhatikan bahawa semasa i₁ masuk, sementara arus i₂ dan saya₃ Mereka keluar.

Oleh itu, undang -undang arus kirchoff membawa kepada persamaan pertama:

1) i₁ - i₂ - i₃ = 0

Nod yang lebih rendah memberikan maklumat yang sama, oleh itu, langkah seterusnya adalah untuk mengembara jejaring.

Mesh pertama

Untuk menubuhkan persamaan berikut, mesh di sebelah kiri dilalui dalam jadual, bermula dari sudut kiri atas. Inilah rasa di mana arus dan arus beredar₁ dan saya₃.

Boleh melayani anda: komparator optik: apa itu dan bahagian

Perhatikan bahawa:

• Yo₁ melalui rintangan 20 Ω, 15 Ω dan 0.5 Ω dan bateri 18 v, di mana dia mengalami potensi kenaikan.
• Bagi bahagiannya, saya₃ Ia melintasi rintangan cawangan pusat 6 Ω dan 0.15 Ω dan pada 3 bateri.0 V adalah kenaikan yang berpotensi.

Begitu juga, undang -undang ohm v = i ∙ r digunakan untuk mewujudkan ketegangan dalam setiap rintangan, menurut ini:

-20 ∙ i₁ - 6 ∙ i₃ + 3.0 - 0.25 ∙ i₃ -15 ∙ i₁ + 18.0 - 0.5 ∙ i₁ = 0

Memesan Terma:

(-20 -15 - 0.5) ∙ i₁ - (6 + 0.25) ∙ i₃  = - 3.0 - 18.0

-35.5 ∙ i₁ - 6.25 ∙ i₃ = - 21.0

2) 5 ∙ i₁ + 6.25 ∙ i₃ = 21.0

Mesh kedua

Persamaan ketiga diperoleh dengan melawat mesh di sebelah kanan, bermula di nod atas litar. Diperhatikan bahawa:

• Yo₂ Melalui rintangan 8 Ω, 0.5 Ω dan 0.75 Ω, ditambah bateri 12 V dan 24 V. Menurut polaritas bateri, dalam laluan terdapat kenaikan potensi dalam 12 V dan penurunan dalam 24 V.
• Penting: Lawatan jejaring kedua (dalam jadual) menentang i₃, Oleh itu, voltan dalam rintangan 6 Ω dan 0.25 Ω berpotensi meningkat dan membawa tanda positif. Menurut polaritas bateri, terdapat kenaikan dalam 12 V dan jatuh pada 24 V dan 3 V.

Dengan semua ini anda mencapai:

-8 ∙ i₂ - 0.5 ∙ i₂ - 0.75 ∙ i₂ + 12.0 - 24.0 + 0.25 ∙ i₃ - 3.0 + 6 ∙ i₃ = 0

3) -25 ∙ i₂ + 6.25 ∙ i₃ = 15.0

Pengiraan semasa

Persamaan 1), 2) dan 3) membentuk sistem 3 persamaan linear dengan 3 tidak diketahui, yang penyelesaiannya adalah:

Yo₁ = 0.381 A; Yo₂ = -0.814 a; Yo₃ = 1.195 a

Tanda negatif semasa i₂ bermaksud bahawa ia mengalir ke arah yang bertentangan skim.