Anggaran Pengukuran Angka Amorf Contoh dan Latihan

The Pengukuran anggaran Daripada angka amorf terdiri daripada satu siri kaedah yang digunakan untuk menentukan kawasan atau perimeter angka geometri yang bukan segitiga, dataran, bulatan, dll. Ada yang boleh diperluaskan kepada angka tiga dimensi.

Pada dasarnya pengukuran terdiri daripada membuat reticulate secara teratur, seperti segi empat tepat, dataran atau trapezoid, yang meliputi kira -kira permukaan. Ketepatan pendekatan kawasan yang diperolehi oleh kaedah ini meningkat dengan kemahiran atau ketumpatan reticulate.

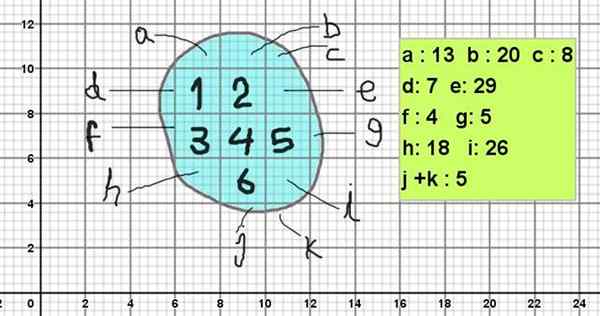
Rajah 1. Batu berbentuk seperti angka amorf. Sumber: Pxfuel.

Angka 1 dan 2 menunjukkan pelbagai angka amorf. Untuk mengira kawasan tersebut, reticulate, terdiri daripada 2 x 2 dataran, yang seterusnya dibahagikan kepada dua puluh lima kotak 2/5 x 2/5.

Menambah kawasan dataran utama dan dataran sekunder kawasan anggaran angka amorf diperolehi.

Rajah 2. Reticulate untuk mengira kawasan salah satu angka amorf dengan cara yang anggaran. Sumber: f. Zapata

[TOC]

Kawasan di bawah lengkung

Sering diperlukan untuk mengira kawasan di bawah lengkung antara dua nilai had. Dalam kes ini, bukannya reticulate persegi, jalur segi empat tepat dapat dikesan kira -kira kawasan di bawah lengkung tersebut.

Jumlah semua jalur segi empat tepat dipanggil Jumlah atau jumlah Riemann. Rajah 3 menunjukkan pemisahan selang [a, b] di mana anda ingin menentukan kira -kira kawasan di bawah lengkung.

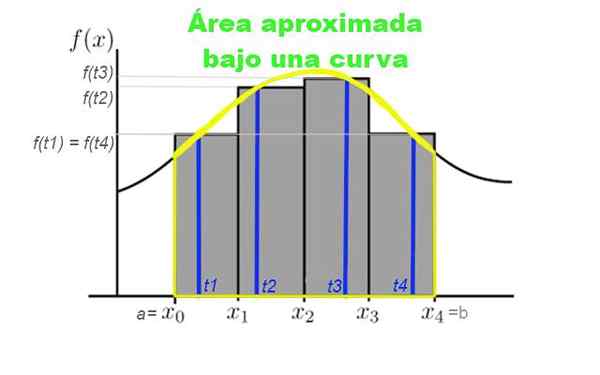Rajah 3. Pemisahan selang [a, b] dalam empat subintervals, yang biasanya diambil dari lebar yang sama. Ketinggian segi empat tepat ditentukan oleh nilai lengkung untuk TK milik subintervals. Sumber: f. Zapata.

Katakan anda ingin mengira kawasan di bawah lengkung yang diberikan oleh fungsi y = f (x), di mana x tergolong dalam selang [a, b] di mana anda ingin mengira kawasan tersebut. Untuk ini, pemisahan elemen N dalam selang ini dibuat:

Boleh melayani anda: 60 pembahagi

Partition = x0 = a, x1, x2, ..., xn = b.

Kemudian kawasan anggaran di bawah lengkung yang diberikan oleh y = f (x) dalam selang [a, b] dicapai dengan jumlah berikut:

S = Σ_{K = 1}ⁿ f (t_k) (x_k - x_K-1)

Di mana t_k adalah antara x_K-1 dan x_k: x_K-1 ≤ t_k ≤ x_k .

Rajah 3 menunjukkan jumlah riemann lengkung y = f (x) dalam selang [x0, x4]. Dalam kes ini, pemisahan empat subinterval dibuat dan jumlahnya mewakili jumlah kawasan segi empat kelabu. 

Jumlah ini mewakili pendekatan ke kawasan di bawah lengkung F antara abscissas x = x0 dan x = x4.

Pendekatan ke kawasan di bawah lengkung bertambah sejauh mana jumlahnya n partition lebih besar, dan cenderung menjadi kawasan di bawah lengkung ketika nombornya n Partition cenderung ke tak terhingga. 

Sekiranya lengkung diwakili oleh fungsi analisis, nilai f (t_k) Mereka dikira menilai fungsi tersebut dalam nilai t_k. Tetapi jika lengkung tidak mempunyai ungkapan analisis, maka kemungkinan berikut tetap:

1. Pendekatan lengkung dengan fungsi, contohnya polinomial.
2. Ambil koordinat Cartesian dari titik di mana lengkung dipintas dengan garis x = t_k.

Selang waktu yang kerap

Bergantung pada pilihan nilai TK dalam selang [x_k, x_K-1], jumlahnya boleh menaksir atau meremehkan nilai tepat kawasan di bawah lengkung fungsi y = f (x). Perkara yang paling dinasihatkan adalah mengambil titik TK di mana kawasan yang hilang adalah kira -kira sama dengan kawasan yang tinggal, walaupun tidak selalu mungkin untuk membuat pilihan sedemikian.  

Boleh melayani anda: songsang berbilang: penjelasan, contoh, latihan yang diselesaikan

Ambil TK pada akhir

Perkara yang paling praktikal adalah menggunakan selang masa yang tetap Δx = (b - a)/n, di mana a dan b adalah nilai minimum dan maksimum abscissa, manakala n adalah bilangan subdivisi.

Dalam kes itu, kawasan di bawah pendekatan lengkung dengan:

Kawasan = f (a+Δx)+f (a+2Δx)+...+f [a+(n-1] Δx+f (b)*Δx

Dalam ungkapan sebelumnya, TK diambil di hujung kanan subinterval.

Ambil TK di hujung kiri

Satu lagi kemungkinan praktikal adalah untuk mengambil nilai TK di hujung kiri, di mana jumlah yang menghampiri kawasan tersebut dinyatakan sebagai:

Kawasan = [f (a)+f (a+Δx)+...+f (a+(n-1) Δx)*Δx

TK sebagai nilai pusat

Dalam kes TK dipilih sebagai nilai pusat subinterval biasa lebar Δx, jumlah yang menghampiri kawasan di bawah lengkung adalah:

Kawasan = [f (a+Δx/2)+f (a+3Δx/2)+...+f (b- Δx/2)]*Δx

Mana -mana ungkapan ini cenderung kepada nilai yang tepat setakat mana bilangan subdivisi sewenang -wenangnya, iaitu Δx cenderung kepada sifar, tetapi dalam hal ini bilangan syarat jumlahnya sangat besar dengan kos pengiraan akibat akibatnya. 

Contoh

Rajah 2 menunjukkan angka amorf, yang konturnya sama dengan batu imej 1. Untuk mengira kawasannya, ia diletakkan di atas reticulate dengan dataran utama 2 x 2 unit ke dataran (contohnya mereka boleh 2 cm²).

Dan kerana setiap persegi dibahagikan kepada 5 x 5 subdivisi, maka setiap subdivisi mempunyai kawasan 0.4 x 0.4 unit persegi (0.16 cm²).

Angka dalam angka akan dikira seperti berikut:

Boleh melayani anda: pemfaktoran biasa: contoh dan latihan

Kawasan = 6 x 2 cm² + (13 + 20 + 8 + 7 + 29 + 4 + 5 + 18 + 26 + 5) x 0.16 cm²

Iaitu:

Kawasan = 12 cm² + 135 x 0.16 cm² = 33.6 cm².

Latihan diselesaikan

Kirakan kira -kira kawasan di bawah lengkung yang diberikan oleh fungsi f (x) = x² Bet A = -2 hingga B = +2. Untuk melakukan ini, tulis jumlah untuk partition tetap selang [a, b] dan kemudian ambil had matematik untuk kes bahawa bilangan partisi cenderung tak terhingga. 

Penyelesaian

Pertama, selang partition ditakrifkan sebagai 

Δx = (b - a)/n. 

Kemudian jumlah yang sesuai dengan fungsi f (x) adalah seperti ini:

A = -2 dan b =+2 diganti supaya selang atau langkah adalah Δx = 4/n. Dalam kes ini jumlah untuk fungsi f (x) = x² adalah:

 Binomial persegi dibangunkan: 

[-2 +(4i/n)]² = 4 - 16 I /n + (4 /n)² Yo²

Dan kemudian ia digantikan dalam jumlah:

Memisahkan penjumlahan dan mengambil jumlah malar sebagai faktor umum setiap jumlah diperolehi:

 Yang pertama dari jumlah, yang kedua adalah:

Dan yang ketiga ialah:

Menggantikan dalam ungkapan jumlah yang anda ada:

S (f, n) = 16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²

Semasa memilih nilai yang besar untuk n, anda mempunyai pendekatan yang baik ke kawasan di bawah lengkung. Walau bagaimanapun, dalam kes ini adalah mungkin untuk mencapai nilai yang tepat mengambil had matematik apabila n cenderung kepada tak terhingga:

Kawasan = lim_{N-> ∞}[16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²]

Kawasan = 16 - (64/2)+ (64/3) = 16/3 = 5.333.

Rujukan

1. Casteleiro, J. M. 2002. Pengiraan Komprehensif (Edisi Illustrated). Madrid: Editorial ESIC.
2. Larson, r. 2010. Pengiraan pemboleh ubah. 9NA. Edisi. McGraw Hill.
3. Purcell, e. 2007. Pengiraan dengan geometri analisis. 9NA. Edisi. Pendidikan Pearson.
4. Unican. Sejarah konsep integral. Pulih dari: repositori.Unican.adalah
5. Uis. Riemann Sums. Pulih dari: matematik.Uis.Edu.co
6. Wikipedia. Kawasan. Pulih dari: Adakah.Wikipedia.com