Langkah -langkah kebolehubahan

Rajah 1.- Langkah kebolehubahan yang paling terkenal. Sumber: f. Zapata.

Apakah langkah -langkah kebolehubahan?

The Langkah -langkah kebolehubahan, Juga dipanggil langkah penyebaran, mereka adalah petunjuk statistik yang menunjukkan sejauh mana atau jauh data aritmetik mereka dijumpai. Sekiranya data hampir dengan purata, pengedarannya tertumpu, dan jika mereka jauh, ia kemudiannya disebarkan.

Terdapat banyak langkah kebolehubahan, antara yang paling terkenal ialah:

• Julat
• Sisihan purata
• Varians
• Sisihan piawai

Langkah -langkah ini melengkapkan langkah -langkah kecenderungan pusat dan perlu memahami pengedaran data yang diperoleh dan mengekstrak sebanyak mungkin maklumat.

Julat

Julat atau laluan mengukur amplitud set data. Untuk menentukan nilainya, perbezaan antara nilai tertinggi x dijumpai_maks dan nilai x paling sedikit_min:

R = x_maks - x_min

Sekiranya data tidak longgar tetapi dikelompokkan oleh selang, maka julat dikira dengan perbezaan antara batas atas selang terakhir dan batas bawah selang pertama.

Apabila julat adalah nilai kecil, ia bermaksud bahawa semua data agak dekat antara satu sama lain, tetapi julat besar menunjukkan bahawa terdapat banyak kebolehubahan. Jelas bahawa, selain dari had atas dan had data yang lebih rendah, julat tidak mengambil kira nilai di antara mereka, jadi tidak digalakkan untuk menggunakannya apabila nombor data adalah besar.

Walau bagaimanapun, adalah langkah segera untuk mengira dan mempunyai unit data yang sama, jadi mudah untuk menafsirkannya.

Contoh pangkat

Seterusnya, senarai ini boleh didapati dengan bilangan matlamat yang ditandakan pada hujung minggu, dalam liga bola sepak dari sembilan negara:

Boleh melayani anda: Apakah pembahagi 30? (Penjelasan)

40, 32, 35, 36, 37, 31, 37, 29, 39

Ia adalah set data tanpa pengelompokan. Untuk mencari julat, mereka terus memerintahkan mereka dari yang paling sedikit ke yang paling besar:

29, 31, 32, 35, 36, 37, 37, 39, 40

Data dengan nilai tertinggi adalah 40 gol dan yang mempunyai nilai terendah adalah 29 gol, oleh itu julatnya adalah:

R = 40-29 = 11 gol.

Boleh dipertimbangkan bahawa julatnya kecil berbanding dengan data nilai minimum, ia.

Sisihan purata

Ukuran kebolehubahan ini dikira melalui purata nilai mutlak penyimpangan berkenaan dengan purata. Menandakan sisihan purata sebagai d_M, Untuk data yang tidak berkumpul, sisihan purata dikira oleh formula berikut:

Di mana n ialah bilangan data yang ada, x_Yo Ia mewakili setiap data dan X̄ adalah purata, yang ditentukan dengan menambahkan semua data dan membahagikan antara n:

Penyimpangan purata membolehkan untuk mengetahui, secara purata, berapa unit data menyimpang dari aritmetik dan mempunyai kelebihan mempunyai unit yang sama seperti data yang berfungsi.

Contoh sisihan tengah

Mengikut data julat, bilangan matlamat yang ditandakan adalah:

40, 32, 35, 36, 37, 31, 37, 29, 39

Sekiranya anda ingin mencari sisihan sederhana d_M Daripada data ini, adalah perlu untuk mengira aritmetik X̄ terlebih dahulu:

Dan sekarang bahawa nilai X̄ diketahui, kita teruskan mencari sisihan purata_M:

= 2.99 ≈ 3 gol

Oleh itu, boleh dikatakan bahawa, secara purata, data bergerak kira -kira dalam 3 matlamat purata iaitu 35 gol, dan seperti yang dinyatakan, ia adalah ukuran yang lebih tepat daripada julat.

Boleh melayani anda: hyperbola

Varians

Penyimpangan purata adalah ukuran kebolehubahan yang lebih nipis daripada julat, tetapi seperti yang dikira melalui nilai mutlak perbezaan antara setiap data dan purata, ia tidak menawarkan fleksibiliti yang lebih besar dari sudut pandangan algebra.

Oleh itu, varians lebih disukai, yang sepadan dengan purata perbezaan kuadratik setiap data dengan min dan dikira menggunakan formula:

Dalam ungkapan ini, s² menandakan varians, dan seperti biasa x_Yo mewakili setiap data, x̄ adalah purata dan n jumlah data.

Apabila bekerja dengan sampel dan bukannya penduduk, lebih suka mengira varians seperti ini:

Perbezaan dengan formula sebelumnya ialah dalam penyebut terdapat n - 1 bukan n. Ia berlaku dengan membahagikan n, varians sampel meremehkan varians penduduk yang mana ia diekstrak, tetapi tidak apabila dibahagikan dengan n - 1. Dalam beberapa teks yang jelas muncul dengan nama Quasi-Variza.

Dalam apa jua keadaan, varians dicirikan dengan sentiasa jumlah yang positif, tetapi purata perbezaan kuadrat, adalah penting untuk memerhatikan bahawa ia tidak mempunyai unit yang sama seperti data.

Contoh varians

Untuk mengira varians data contoh julat dan sisihan purata, nilai yang sepadan diganti dan jumlah yang ditunjukkan. Dalam kes ini, ia dipilih untuk membahagikan antara N-1:

= 13.86

Sisihan piawai

Varians tidak mempunyai unit yang sama dengan pembolehubah yang sedang dikaji, sebagai contoh, jika data datang dalam meter, varians menghasilkan meter persegi. Atau dalam contoh matlamat, ia akan menjadi matlamat yang sama, yang tidak masuk akal.

Boleh melayani anda: apakah unsur -unsur perumpamaan? (Bahagian)

Oleh itu, sisihan piawai ditakrifkan, juga dipanggil Penyimpangan biasa, Seperti akar kuadrat varians:

S = √s²

Dengan cara ini ukuran kebolehubahan data diperolehi dalam unit yang sama seperti ini, dan semakin rendah nilai s, semakin banyak dikumpulkan data adalah sekitar purata.

Kedua -dua varians dan sisihan piawai adalah langkah -langkah kebolehubahan yang akan dipilih apabila aritmetik adalah ukuran kecenderungan pusat yang paling menggambarkan tingkah laku data.

Dan adalah bahawa sisihan piawai mempunyai harta yang penting, yang dikenali sebagai teorem Chebyshev: sekurang -kurangnya 75% pemerhatian berada dalam selang yang ditakrifkan oleh x̄ ± 2s. Dengan kata lain, 75% daripada data adalah, paling banyak, pada jarak yang sama dengan 2s sekitar purata.

Begitu juga, sekurang -kurangnya 89% nilai berada pada jarak 3 dari purata, peratusan yang dapat diperluas, dengan syarat banyak data tersedia dan ini mengikuti taburan normal.

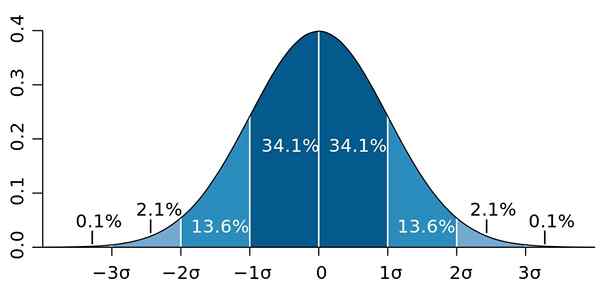
Rajah 2.- Sekiranya data mengikuti taburan normal, 95.4 daripadanya adalah dua sisihan piawai di kedua -dua belah purata. Sumber: Wikimedia Commons.

Contoh sisihan piawai

Penyimpangan piawai data yang dibentangkan dalam contoh sebelumnya ialah:

S = √s² = √13.86 = 3.7 ≈ 4 gol