Pengagihan ciri dan latihan diselesaikan

The Pengagihan f o Pengagihan Fisher-Snedecor adalah apa yang digunakan untuk membandingkan variasi dua populasi yang berbeza atau bebas, yang masing-masing mengikuti taburan biasa.

Pengagihan yang mengikuti varians satu set sampel populasi normal tunggal ialah taburan Ji-Square (Χ²) darjah n-1, jika setiap sampel set mempunyai elemen n.

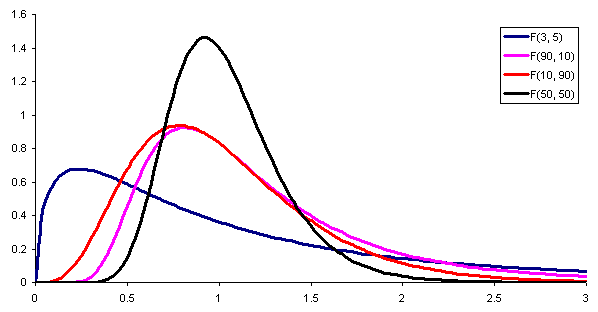
Rajah 1. Berikut adalah ketumpatan kebarangkalian pengedaran F dengan kombinasi parameter (atau darjah kebebasan) pengangka dan penyebut masing -masing. Sumber: Wikimedia Commons.

Untuk membandingkan variasi dua populasi yang berbeza, perlu untuk menentukan a statistik, iaitu pemboleh ubah rawak tambahan yang membolehkan untuk membezakan sama ada kedua -dua populasi mempunyai atau tidak varians yang sama.

Pemboleh ubah tambahan ini boleh secara langsung adalah kuota variasi sampel bagi setiap populasi, yang mana, jika dikatakan kuota dekat dengan unit, dibuktikan bahawa kedua -dua populasi mempunyai variasi yang sama.

[TOC]

Statistik f dan taburan teorinya

Pembolehubah rawak f atau statistik F yang dicadangkan oleh Ronald Fisher (1890 - 1962) adalah yang digunakan lebih kerap untuk membandingkan variasi dua populasi dan ditakrifkan sebagai berikut:

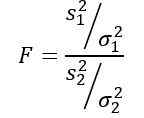
Menjadi s² Varians sampel dan σ² Varians penduduk. Untuk membezakan setiap dua kumpulan penduduk, langganan 1 dan 2 digunakan masing -masing.

Adalah diketahui bahawa pengedaran Ji-square dengan (n-1) darjah kebebasan adalah yang mengikuti pembolehubah tambahan (atau statistik) yang ditakrifkan di bawah:

X² = (N-1) s² / σ².

Oleh itu, statistik F mengikuti taburan teori yang diberikan oleh formula berikut:

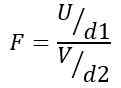
Menjadi Atau Pengedaran ji-persegi dengan D1 = n1 - 1 darjah kebebasan untuk penduduk 1 dan V Pengedaran ji-persegi dengan D2 = n2 - 1 darjah kebebasan untuk penduduk 2.

Boleh melayani anda: aljabar vektor

Nisbah yang ditakrifkan dengan cara ini adalah taburan kebarangkalian baru, yang dikenali sebagai Pengagihan f dengan D1 darjah kebebasan dalam pengangka dan D2 darjah kebebasan dalam penyebut.

Purata, fesyen dan varians pengedaran f

Separuh

Pengagihan purata F dikira seperti berikut:

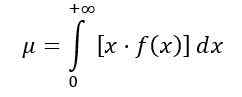
Menjadi f (x) ketumpatan kebarangkalian pengedaran f, yang ditunjukkan dalam Rajah 1 untuk beberapa kombinasi parameter atau darjah kebebasan.

Anda boleh menulis ketumpatan kebarangkalian f (x) bergantung kepada fungsi γ (fungsi gamma):

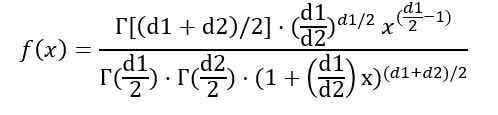
Sebaik sahaja integral ditunjukkan sebelum ini, disimpulkan bahawa purata pengedaran f dengan darjah kebebasan (d1, d2) adalah: adalah: adalah: adalah:

μ = d2 / (d2 - 2) dengan d2> 2

Di mana ia menunjukkan bahawa, dengan penuh rasa ingin tahu, purata tidak bergantung pada tahap kebebasan d1 pengangka.

Fesyen

Sebaliknya, fesyen bergantung kepada D1 dan D2 dan diberikan oleh:

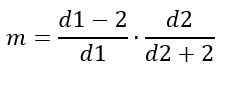
Untuk d1> 2.

Varians pengedaran f

Varians σ² pengedaran f dikira dari integral:

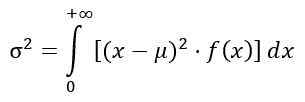
Memperoleh:

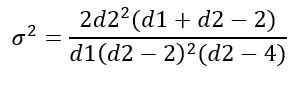
Pengurusan Pengedaran f

Seperti pengagihan kebarangkalian berterusan lain yang melibatkan fungsi rumit, pengurusan pengedaran F dilakukan oleh jadual atau oleh perisian.

Jadual pengedaran f

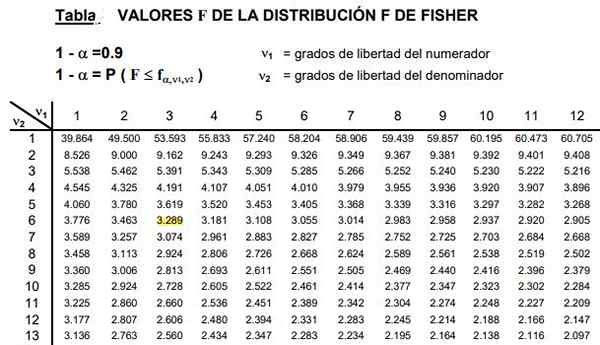Rajah 2. Sebahagian daripada jadual pengedaran F ditunjukkan, yang biasanya sangat luas kerana terdapat kombinasi yang luas dari kemungkinan kebebasan D1 dan D2.

Jadual -jadual melibatkan dua parameter atau darjah kebebasan pengedaran f, lajur menunjukkan tahap kebebasan pengangka dan baris tahap kebebasan penyebut.

Boleh melayani anda: Ketidaksamaan segitiga: demonstrasi, contoh, latihan yang diselesaikan

Rajah 2 menunjukkan seksyen jadual pengedaran f untuk kes a tahap kepentingan 10%, iaitu α = 0.1. Nilai f diserlahkan apabila d1 = 3 dan d2 = 6 dengan tahap keyakinan 1- α = 0.9 iaitu 90%.

Perisian untuk pengedaran f

Bagi perisian yang menguruskan pengedaran f terdapat pelbagai jenis, dari spreadsheet sebagai Excel Malah pakej khusus seperti Minitab, SPSS dan R Untuk menamakan beberapa yang paling terkenal.

Harus diperhatikan bahawa perisian geometri dan matematik Geogebra Ia mempunyai alat statistik yang merangkumi pengagihan utama, termasuk pengedaran f. Rajah 3 menunjukkan pengedaran f untuk kes d1 = 3 dan d2 = 6 tahap keyakinan 90%.

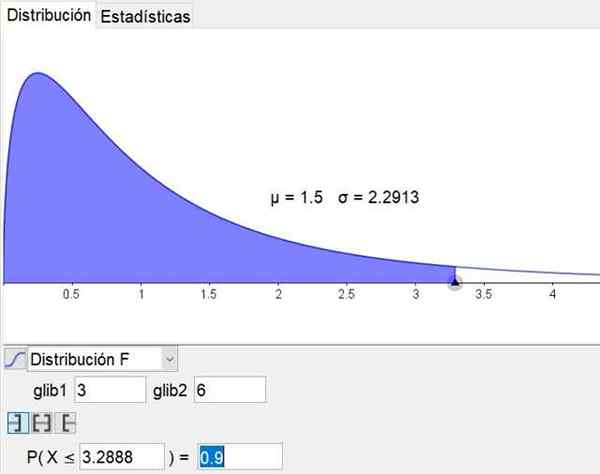Rajah 3. Pengagihan F ditunjukkan untuk kes d1 = 3 dan d2 = 6 dengan tahap keyakinan 90%, diperolehi melalui alat statistik geogra. Sumber: Geogebra.org

Latihan yang diselesaikan

Latihan 1

Pertimbangkan dua contoh populasi yang mempunyai varians penduduk yang sama. Jika sampel 1 adalah saiz n1 = 5 dan sampel 2 adalah saiz n2 = 10, tentukan kebarangkalian teoritis bahawa nisbah varians masing -masing kurang dari atau sama dengan 2.

Penyelesaian

Harus diingat bahawa statistik f ditakrifkan sebagai:

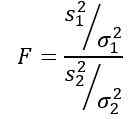
Tetapi kita diberitahu bahawa variasi penduduk adalah sama, jadi untuk latihan ini ia terpakai:

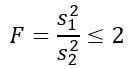
Seperti yang anda ingin tahu kebarangkalian teori bahawa nisbah variasi sampel ini kurang daripada atau sama dengan 2, kita perlu mengetahui kawasan di bawah pengedaran F antara 0 dan 2, yang boleh diperolehi oleh jadual atau perisian. Untuk ini, perlu diambil kira bahawa pengedaran yang diperlukan f mempunyai d1 = n1 - 1 = 5 - 1 = 4 dan d2 = n2 - 1 = 10 - 1 = 9, iaitu pengedaran f dengan darjah kebebasan (4, 9).

Ia boleh melayani anda: Siri Kuasa: Contoh dan Latihan

Dengan menggunakan alat statistik Geogebra Ia ditentukan bahawa kawasan ini adalah 0.82, jadi disimpulkan bahawa kebarangkalian bahawa nisbah variasi sampel kurang dari atau sama dengan 2 adalah 82%.

Senaman 2

Terdapat dua proses pembuatan lembaran nipis. Kebolehubahan ketebalan mestilah sebanyak mungkin. 21 sampel setiap proses diambil. Sampel proses mempunyai sisihan piawai sebanyak 1.96 mikron, manakala proses B mempunyai sisihan piawai sebanyak 2.13 mikron. Yang manakah proses mempunyai kebolehubahan yang lebih rendah? Gunakan tahap penolakan 5%.

Penyelesaian

Data adalah seperti berikut: SB = 2.13 dengan NB = 21; SA = 1.96 dengan NA = 21. Ini bermaksud bahawa anda harus bekerja dengan pengedaran f (20, 20) darjah kebebasan.

Hipotesis nol menunjukkan bahawa varians populasi kedua -dua proses adalah sama, iaitu, σa^2 / σb^2 = 1. Hipotesis alternatif akan menyiratkan variasi penduduk yang berbeza.

Kemudian, di bawah anggapan variasi populasi yang sama, statistik f dikira sebagai: fc = (sb/sa)^2 ditakrifkan.

Oleh kerana tahap penolakan telah diambil sebagai α = 0.05, maka α/2 = 0.025

Pengedaran f (0.025; 20,20) = 0.406, manakala F (0.975; 20,20) = 2.46.

Oleh itu, hipotesis nol akan benar jika F dikira mematuhi: 0.406≤FC≤2,46. Jika tidak, hipotesis nol ditolak.

Sebagai FC = (2,13/1.96)^2 = 1.18 disimpulkan bahawa statistik FC berada dalam julat penerimaan hipotesis nol dengan kepastian 95%. Dengan kata lain dengan kepastian 95% kedua -dua proses pembuatan mempunyai varians penduduk yang sama.

Rujukan

1. F Ujian Kemerdekaan. Pulih dari: Saylordotorg.Github.Io.
2. Gelombang med. Statistik yang digunakan untuk sains kesihatan: Ujian f. Pulih dari: medwave.Cl.
3. Kebarangkalian dan statistik. Pengagihan f. Diperolehi daripada: Kebarangkalian Andestik.com.
4. Triola, m. 2012. Statistik asas. 11hb. Edisi. Addison Wesley.
5. Unam. Pengagihan f. Pulih dari: nasihat.CUAutitlan2.Unam.mx.
6. Wikipedia. Pengagihan f. Pulih dari: Adakah.Wikipedia.com