Sekurang -kurangnya dataran

Apakah kaedah dataran minimum?

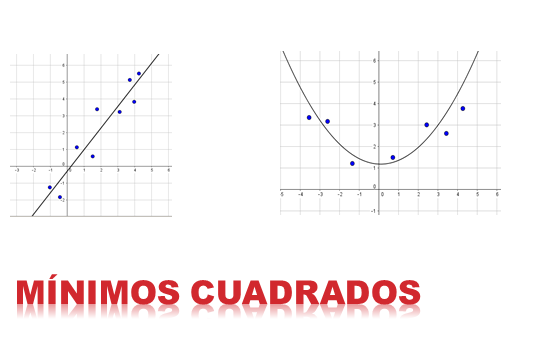
Kaedah Sekurang -kurangnya dataran Ini adalah salah satu aplikasi yang paling penting dalam pendekatan fungsi. Idea ini adalah untuk mencari lengkung seperti itu, diberi satu set pasangan yang kemas, fungsi ini lebih baik didekati dengan data. Fungsi ini boleh menjadi garis, lengkung kuadrat, kubik, dan lain -lain.

Idea kaedah ini adalah untuk meminimumkan jumlah kuadrat perbezaan dalam ordinat (komponen y), antara titik yang dihasilkan oleh fungsi yang dipilih dan titik milik set data.

Kaedah minimum persegi

Sebelum memberikan kaedah, kita mesti terlebih dahulu jelas tentang apa yang "lebih baik menghampiri". Katakan garis dicari y = b+mx yang terbaik yang mewakili satu set titik n, iaitu (x1, y1), (x2, y2) ..., (xn, yn).

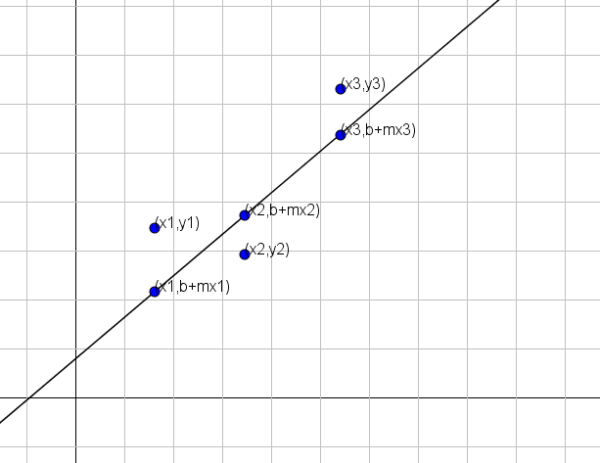
Seperti yang ditunjukkan dalam angka sebelumnya, jika pembolehubah x dan y dikaitkan dengan garis y = b+mx, maka untuk x = x1 nilai yang sama y akan b+mx1. Walau bagaimanapun, nilai ini berbeza daripada nilai sebenar y, iaitu y = y1.

Ingatlah bahawa dalam pesawat, jarak antara dua mata diberikan oleh formula berikut:

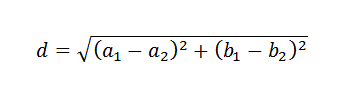
Dengan ini, untuk menentukan cara memilih garis y = b+mx yang terbaik mendekati data yang diberikan, kedengarannya logik untuk digunakan sebagai kriteria pemilihan garis yang meminimumkan jumlah kuadrat jarak antara titik dan garis.

Oleh kerana jarak antara titik (x1, y1) dan (x1, b+mx1) adalah y1- (b+mx1), masalah kami dikurangkan untuk mencari nombor m dan b supaya jumlah yang akan datang adalah minimum:

Boleh melayani anda: teorem hijau, demonstrasi, aplikasi dan latihan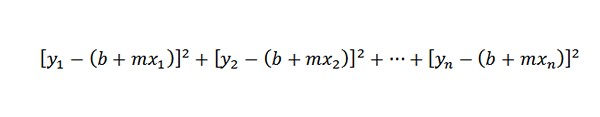

Barisan yang memenuhi syarat ini dikenali sebagai "pendekatan ke garis kotak minimum ke titik (x1, y1), (x2, y2), ..., (xn, yn)".

Sebaik sahaja masalah diperoleh, ia hanya tetap memilih kaedah untuk mencari pendekatan dengan dataran minimum. Jika mata (x1, y1), (x2, y2), ..., (xn, yn) semuanya berada di garisan y = mx+b, kita perlu menjadi colineal dan:

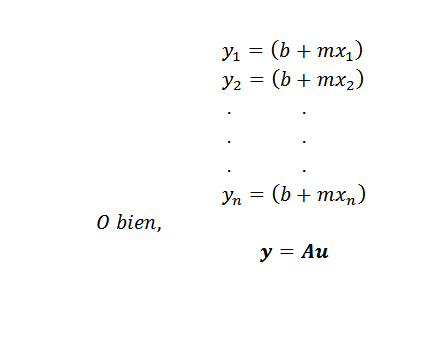
Dalam ungkapan ini:

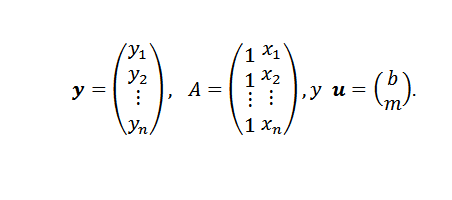
Akhirnya, jika titik tidak colineal, maka y-au = 0 dan masalahnya dapat diterjemahkan ke dalam mencari vektor atau sedemikian rupa sehingga standard Euclidean adalah minimum.

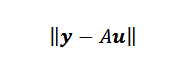
Mencari vektor yang meminimumkan atau tidak sukar seperti yang anda fikirkan. Sebagai A adalah matriks Nx2 dan U adalah matriks 2 × 1, kita mempunyai bahawa vektor au adalah vektor dalam r dalam rⁿ dan tergolong dalam imej A, yang merupakan ruang bawah R Rⁿ Dengan dimensi tidak lebih dari dua.

Kami akan mengandaikan bahawa n = 3 untuk menunjukkan apakah prosedur yang mesti diikuti. Sekiranya n = 3, imej A akan menjadi satah atau garis yang melalui asal.

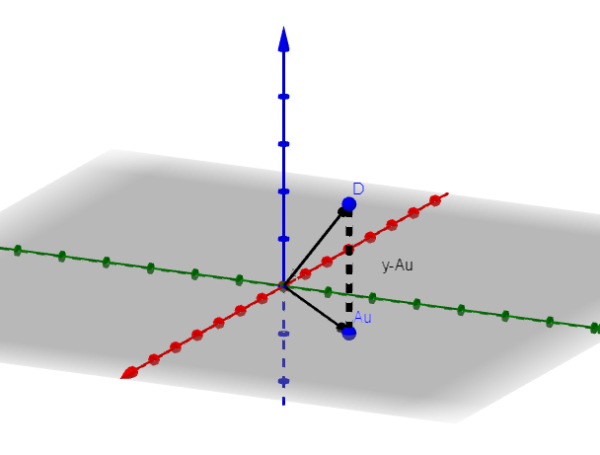
Biarkan v vektor meminimumkan. Dalam angka kita melihat bahawa y-au diminimumkan apabila ia ortogonal dengan imej a. Iaitu, jika v adalah vektor yang meminimumkan, maka ia berlaku:

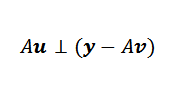
Kemudian, kita dapat menyatakan perkara di atas dengan cara ini:

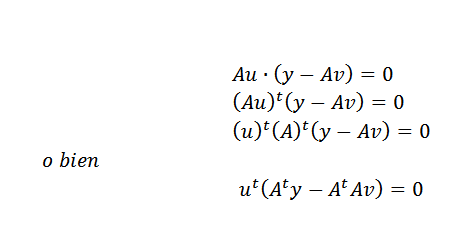
Ini hanya boleh berlaku jika:

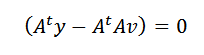
Akhirnya, membersihkan V, kita perlu:

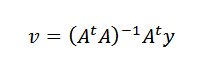
Adalah mungkin untuk melakukan ini sejak itu^tA boleh terbalik apabila n mata sebagai data bukan colineal.

Sekarang, jika bukannya mencari garis kita ingin mencari perumpamaan (ekspresi yang akan menjadi bentuk y = a+bx+cx²) Bahawa ia adalah penghampiran yang lebih baik kepada titik data, prosedur akan diterangkan di bawah.

Boleh melayani anda: keseluruhan nombor

Sekiranya titik data berada dalam perumpamaan itu, ia perlu:

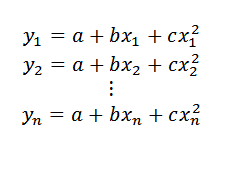
Kemudian:

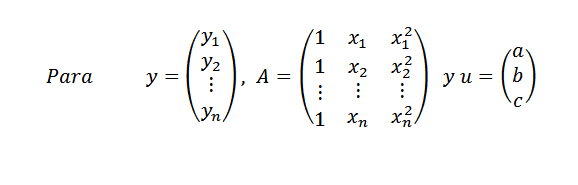
Begitu juga kita boleh menulis y = au. Sekiranya semua mata tidak ada dalam perumpamaan, kami mempunyai y-au berbeza dari sifar untuk mana-mana vektor u dan masalah kami sekali lagi: cari vektor u dalam r3 supaya norma || y-au || sebanyak mungkin.

Mengulangi prosedur sebelumnya, kita boleh sampai ke vektor yang dikehendaki adalah:

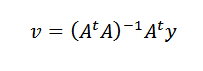
Latihan yang diselesaikan

Latihan 1

Cari garis yang paling sesuai dengan mata (1.4), (-2.5), (3, -1) dan (4.1).

Penyelesaian

Kita mesti:

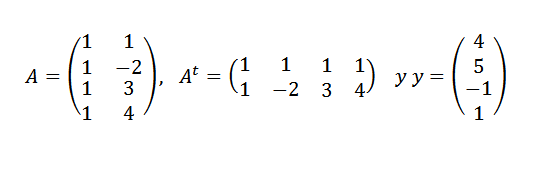
Kemudian:

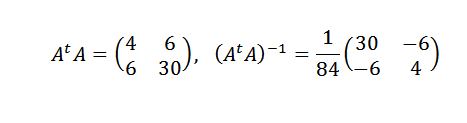
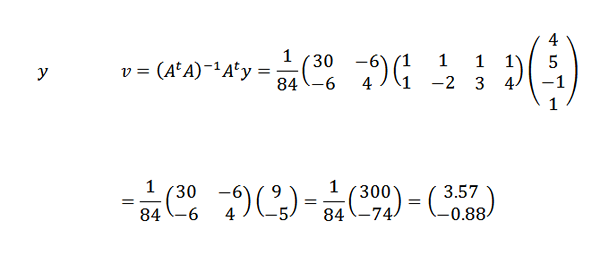
Oleh itu, kami menyimpulkan bahawa garis yang paling sesuai dengan mata yang diberikan oleh:

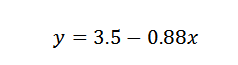
Latihan 2

Katakan objek dijatuhkan dari ketinggian 200 m. Semasa jatuh, langkah -langkah berikut diambil:

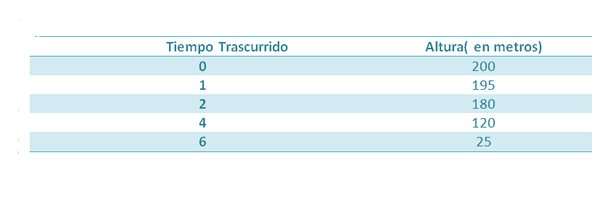
Kami tahu bahawa ketinggian objek ini, selepas masa telah berlalu, diberikan oleh:

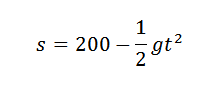
Sekiranya kita ingin mendapatkan nilai g, kita boleh mencari perumpamaan yang merupakan pendekatan yang lebih baik untuk lima mata yang diberikan dalam jadual, dan oleh itu kita akan mempunyai pekali yang mengiringi t² Ia akan menjadi pendekatan yang munasabah untuk (-1/2) g jika pengukuran tepat.

Kita mesti:

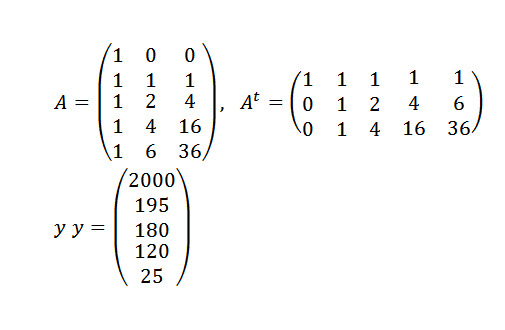
Dan kemudian:

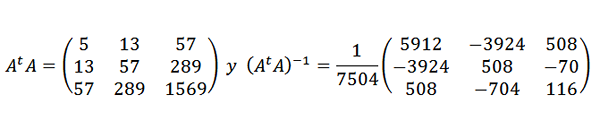
Jadi titik data diselaraskan oleh ungkapan kuadrat berikut:

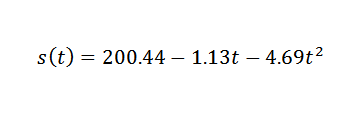
Jadi anda mesti:

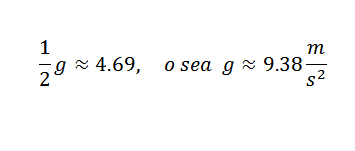
Ini adalah nilai yang cukup dekat dengan yang betul, iaitu g = 9.81 m/s². Untuk mendapatkan g g yang lebih tepat, perlu bermula dari pemerhatian yang lebih tepat.

Apakah kaedah minimum persegi untuk?

Dalam masalah yang berlaku dalam sains semula jadi atau sosial, mudah untuk menulis hubungan antara pembolehubah yang berbeza melalui beberapa ungkapan matematik.

Boleh melayani anda: variasi berkadar

Sebagai contoh, kita boleh mengaitkan dalam ekonomi kos (c), pendapatan (i) dan keuntungan (u) melalui formula mudah:

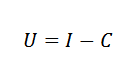
Dalam fizik, kita boleh mengaitkan pecutan yang disebabkan oleh graviti, masa di mana objek telah jatuh dan ketinggian objek oleh undang -undang:

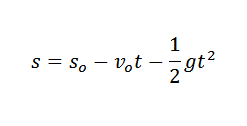
Dalam ungkapan sebelumnya s_{Sama ada} Ia adalah ketinggian awal objek tersebut dan v_{Sama ada} Adakah kelajuan awal anda.

Walau bagaimanapun, mencari formula seperti ini bukan tugas mudah; Ia biasanya sepadan dengan profesional yang bertugas untuk bekerja dengan banyak data dan berulang kali menjalankan beberapa eksperimen (untuk mengesahkan bahawa hasil yang diperoleh adalah malar) untuk mencari hubungan antara data yang berbeza.

Cara yang sama untuk mencapai matlamat ini adalah untuk mewakili data yang diperolehi dalam pesawat sebagai titik dan mencari fungsi berterusan yang secara optimum mendekati perkara ini.

Salah satu cara untuk mencari fungsi yang "pendekatan yang lebih baik" data yang diberikan adalah dengan kaedah minimum persegi.

Di samping itu, seperti yang kita lihat dalam latihan ini, terima kasih kepada kaedah ini, kita dapat mencapai pendekatan yang cukup dekat dengan pemalar fizikal.