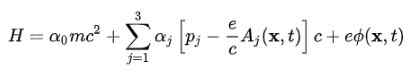Model Aomic ciri -ciri dan postulat Dirac Jordan

Dia Model Atom Dirac-Jordan Ini adalah penyebaran relativistik pengendali Hamiltonian dalam persamaan yang menggambarkan fungsi gelombang kuantum. Tidak seperti model sebelumnya, Schrodinger, tidak perlu mengenakan putaran melalui prinsip pengecualian Pauli, kerana ia kelihatan secara semula jadi.

Di samping itu, model Dirac-Jordan menggabungkan pembetulan relativistik, interaksi spin-organ dan istilah Darwin, yang menyumbang struktur halus tahap elektronik atom.

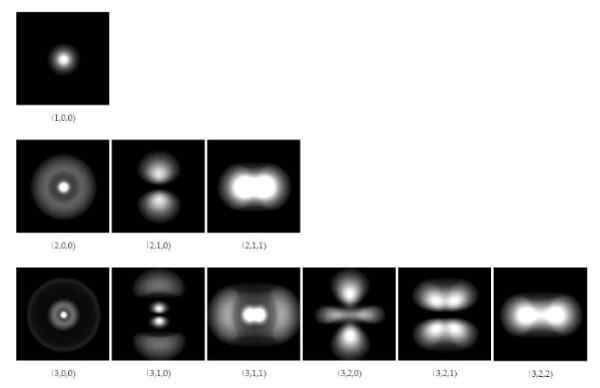
Rajah 1. Orbital elektronik dalam atom hidrogen untuk tiga tahap tenaga pertama. Sumber: Wikimedia Commons.

Sehingga tahun 1928, saintis Paul A. M. Dirac (1902-1984) dan Pascual Jordan (1902-1980), dicadangkan untuk menyebarkan mekanik kuantum yang dibangunkan oleh Schrodinger, untuk memasukkan pembetulan relativiti khas Einstein.

Sebahagian daripada persamaan Schrodinger, yang terdiri daripada pengendali pembezaan, yang dipanggil Hamiltonian, yang beroperasi pada fungsi yang dikenali sebagai Fungsi gelombang elektron. Walau bagaimanapun, Schrodinger tidak mengambil kira kesan relativistik.

Penyelesaian fungsi gelombang membolehkan untuk mengira kawasan di mana elektron di sekitar nukleus akan dijumpai dengan tahap kebarangkalian tertentu. Kawasan atau kawasan ini dipanggil Orbital Dan mereka bergantung pada nombor kuantum diskret tertentu, yang menentukan momentum tenaga dan sudut elektron. 

[TOC]

Postulates

Dalam teori mekanikal kuantum, sama ada relativistik atau tidak, tidak ada konsep orbit, kerana kedudukan atau kelajuan elektron tidak dapat ditentukan secara serentak. Dan di samping itu, menentukan salah satu pembolehubah membawa kepada jumlah ketepatan yang lain.

Bagi pihaknya, Hamiltonian adalah pengendali matematik yang bertindak pada fungsi gelombang kuantum dan dibina dari tenaga elektron. Contohnya, elektron bebas mempunyai tenaga dan bergantung pada momentum linearnya p Oleh itu:

E = (p²)/ 2m

Untuk membina Hamiltonian, ia bermula dari ungkapan ini dan diganti p Oleh pengendali kuantum untuk momentum: 

p = -I ħ ∂ /∂r 

Penting untuk diperhatikan bahawa istilahnya p dan p Mereka berbeza, kerana yang pertama adalah momentum dan yang lain adalah Pengendali pembezaan dikaitkan dengan momentum. 

Boleh melayani anda: Model atom leukipo: postulates, batasan, kepentingan

Di samping itu, saya adalah unit khayalan dan ħ pemalar planck dibahagikan dengan 2π, dengan cara ini pengendali Hamiltonian H dari elektron bebas diperoleh:

H = (ħ²/2m) ∂² /∂r² 

Untuk mencari Hamiltonian elektron dalam atom, interaksi elektron dengan nukleus ditambah: 

H = (ħ2/2m) ∂² /∂r²  - Eφ (r)

Dalam ekspresi sebelumnya -e adalah caj elektrik elektron dan φ (r) potensi elektrostatik yang dihasilkan oleh nukleus pusat.

Sekarang, pengendali H bertindak pada fungsi gelombang ψ mengikut persamaan Schrodinger, yang ditulis seperti ini:

H ψ = (i ħ ∂ /∂t) ψ

Empat postulates Dirac

Postulat pertama: Persamaan gelombang relativistik mempunyai struktur yang sama dengan persamaan gelombang Schrodinger, apakah perubahan h:

H ψ = (i ħ ∂ /∂t) ψ

Postulat kedua: Pengendali Hamiltonian dibina berdasarkan hubungan momentum tenaga Einstein, yang ditulis seperti ini:

E = (m² c⁴ + p² c²)^1/2

Dalam hubungan sebelumnya, jika zarah mempunyai momentum p = 0 maka anda mempunyai persamaan yang terkenal e = mc² yang mengaitkan tenaga berehat dari jisim jisim m dengan kelajuan cahaya c.

Postulat ketiga: Untuk mendapatkan pengendali Hamiltonian, peraturan kuantisasi yang sama yang digunakan dalam persamaan Schrodinger digunakan:

p = -I ħ ∂ /∂r

Pada mulanya, tidak jelas bagaimana untuk mengendalikan pengendali pembezaan ini yang bertindak dalam akar persegi, jadi Dirac berangkat untuk mendapatkan pengendali Hamiltonian linear di pengendali momentum dan dari sana muncul postulat keempatnya.

Bilik postulat: Untuk menghilangkan akar kuadrat dalam formula tenaga relativistik, Dirac mencadangkan struktur berikut untuk e²:

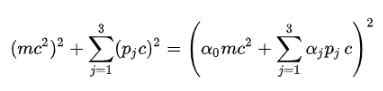
Sudah tentu, perlu menentukan pekali alfa (α0, α1, α2, α3) sehingga ini dipenuhi.

Persamaan Dirac

Persamaan Dirac pertama kali dibangkitkan untuk elektron bebas, menggunakan struktur yang dicadangkan di postulat keempat. Ia tetap seperti berikut: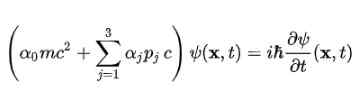

Ia dapat melayani anda: mendengar kekuatan: permukaan dan kekuatan massa

Dalam bentuk padatnya, persamaan Dirac dianggap sebagai salah satu persamaan matematik yang paling indah di dunia:

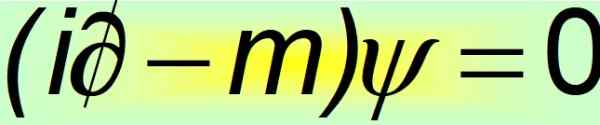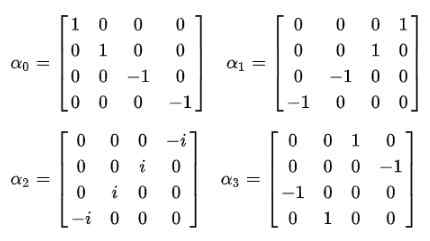
Rajah 2. Persamaan Dirac padat. Sumber: f. Zapata.

Dan itulah apabila dibuktikan bahawa alfas tetap tidak boleh menjadi jumlah skalar. Satu -satunya cara di mana kesamaan postulat keempat dipenuhi adalah bahawa mereka adalah matriks tetap 4 × 4, yang dikenali sebagai Matriks Dirac:

Ia segera diperhatikan bahawa fungsi gelombang berhenti menjadi fungsi skalar dan menjadi vektor empat komponen Espinor:

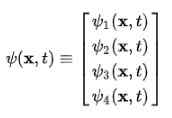
Atom Dirac-Jordan

Untuk mendapatkan model atom, perlu bergerak dari persamaan elektron bebas ke elektron dalam medan elektromagnet yang dihasilkan oleh nukleus atom. Interaksi ini diambil kira dengan memasukkan potensi skalar φ dan vektor yang berpotensi Ke Di Hamiltonian:

Fungsi Gelombang (Espinor) yang dihasilkan daripada menggabungkan Hamiltonian ini mempunyai ciri -ciri berikut: 

- Ia memenuhi relativiti khas, kerana ia mengambil kira tenaga intrinsik elektron (istilah pertama Hamiltonian relativistik)

- Ia mempunyai empat penyelesaian yang sepadan dengan empat komponen Espinor

- Dua penyelesaian pertama sesuai dengan satu hingga putaran +½ dan yang lain ke putaran - ½ 

- Akhirnya, dua penyelesaian yang lain meramalkan kewujudan antimatter, kerana mereka sesuai dengan positrons yang bertentangan.

Kelebihan persamaan Dirac ialah pembetulan Hamiltonian asas Schrodinger H (O) boleh dipecahkan kepada beberapa istilah yang akan kita tunjukkan di bawah:

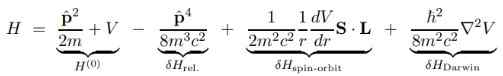
Dalam ungkapan sebelumnya V adalah skalar yang berpotensi, kerana vektor yang berpotensi Ke Ia tidak sah jika sepatutnya menjadi proton pegun pusat dan itulah sebabnya ia tidak muncul.

Sebab mengapa pembetulan Dirac mengenai penyelesaian Schrodinger dalam fungsi gelombang adalah halus. Mereka timbul dari fakta bahawa tiga syarat terakhir Hamiltonian yang diperbetulkan semuanya dibahagikan dengan kelajuan C dari persegi, jumlah yang besar, yang menjadikan istilah ini secara berangka kecil.

Ia dapat melayani anda: vy canis majoris: penemuan, ciri, struktur, latihan dan evolusi

Pembetulan relativistik ke spektrum tenaga

Menggunakan persamaan DIC-Jordan, pembetulan didapati pada spektrum tenaga elektron dalam atom hidrogen. Terdapat juga pembetulan tenaga dalam atom dengan lebih daripada satu elektron kira -kira melalui metodologi yang dikenali sebagai teori gangguan.

Begitu juga, model Dirac membolehkan anda mencari pembetulan struktur halus pada tahap tenaga hidrogen. 

Walau bagaimanapun, pembetulan yang lebih halus seperti struktur hyperfine dan peralihan kambing diperolehi daripada model yang lebih maju seperti Teori Quantum Campos, Dilahirkan tepat kerana sumbangan model Dirac.

Angka berikut menunjukkan bagaimana pembetulan relativistik Dirac berada pada tahap tenaga:

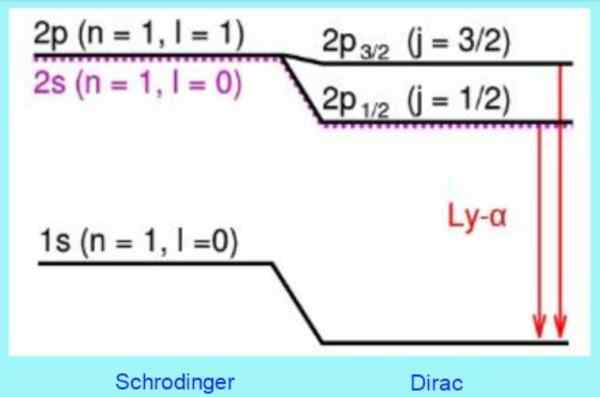Rajah 3. Pembetulan Model Dirac pada tahap atom hidrogen. Sumber: Wikimedia Commons.

Sebagai contoh, penyelesaian kepada persamaan Dirac dengan betul meramalkan peralihan yang diperhatikan pada tahap 2s. Ia adalah pembetulan struktur halus yang terkenal di garis Lyman - alfa spektrum hidrogen (lihat Rajah 3).

Dengan cara ini, struktur halus adalah nama yang menerima fizik atom yang berlaku dari garis -garis spektrum pelepasan atom, yang merupakan akibat langsung dari putaran elektronik.

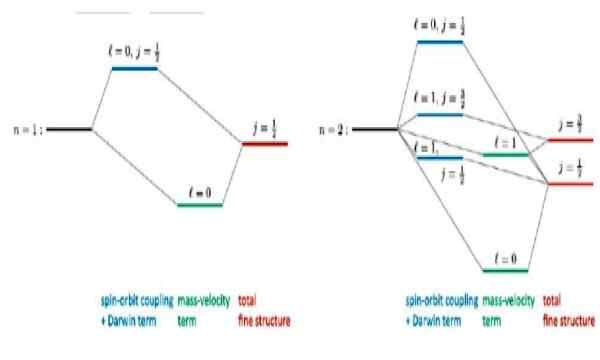Rajah 4. Struktur halus yang berlaku untuk keadaan asas n = 1 dan keadaan teruja pertama n = 2 dalam atom hidrogen. Sumber: r wirnata. Pembetulan relativistik ke atom seperti hidrogen. Penyelidikan.jaring

Artikel yang menarik

Model Broglie Atom.

Model Atom Chadwick.

Model Atom Heisenberg.

Model atom Perrin.

Model Thomson Atom.

Model Atom Dalton.

Model atom Schrödinger.

Model Atom Democritus.

Model Atom Leucipo.

Model Atom Bohr.

Model atom semasa.

Rujukan

1. Teori atom. Pulih dari Wikipedia.org.
2. Momen magnet elektron. Pulih dari Wikipedia.org.
3. Quanta: Buku Panduan Konsep. (1974). Oxford University Press. Pulih dari Wikipedia.org.
4. Model Atom Dirac Jordan. Pulih dari Prezi.com.
5. Alam semesta kuantum baru. Cambridge University Press. Pulih dari Wikipedia.org.