Matematik

Kaedah Gauss-Seidel Penjelasan, Aplikasi, Contoh

Kaedah Gauss-Seidel Penjelasan, Aplikasi, Contoh

Dia Kaedah Gauss-Seidel Ini adalah prosedur berulang untuk mencari penyelesaian anggaran kepada sistem persamaan algebra linear dengan ketepatan yang dipilih sewenang -wenang. Kaedah ini terpakai kepada matriks persegi dengan unsur -unsur yang tidak null dalam pepenjuru dan konvergensi dijamin jika matriks dominan diagonal.

Ia dicipta oleh Carl Friedrich Gauss (1777-1855), yang membuat demonstrasi peribadi kepada salah seorang pelajarnya pada tahun 1823. Seterusnya ia diterbitkan secara rasmi oleh Philipp Ludwig von Seidel (1821-1896) pada tahun 1874, oleh itu nama kedua-dua ahli matematik.

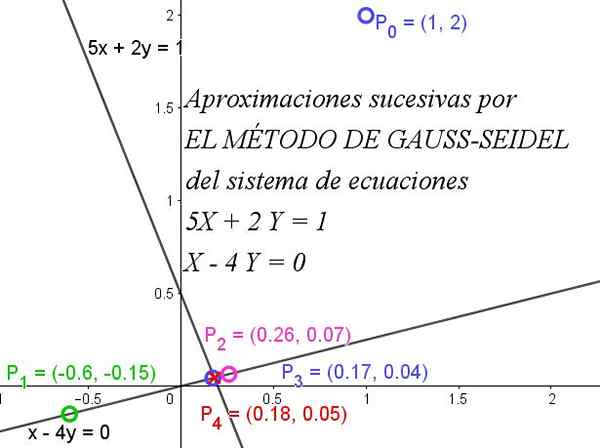
Rajah 1. Kaedah Gauss-Seidel dengan cepat menumpu untuk mendapatkan sistem persamaan. Sumber: f. Zapata.

Untuk pemahaman penuh tentang kaedah ini, perlu mengetahui bahawa matriks adalah dominan diagonal apabila nilai mutlak unsur pepenjuru setiap baris adalah lebih besar daripada atau sama dengan jumlah nilai mutlak unsur -unsur lain dari baris yang sama.

Secara matematik ia dinyatakan seperti berikut:

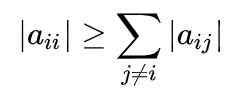
[TOC]

Penjelasan melalui kes yang mudah

Untuk menggambarkan apa kaedah Gauss-Seidel akan mengambil kes yang mudah, di mana anda dapat mencari nilai x dan y dalam sistem persamaan linear 2 × 2 yang ditunjukkan di bawah:

5x + 2y = 1

X - 4y = 0

Langkah -langkah untuk diikuti

1- pertama sekali anda perlu menentukan sama ada penumpuan adalah selamat. Ia segera diperhatikan bahawa, pada dasarnya, ia adalah sistem yang dominan diagonal, kerana pada baris pertama pekali pertama mempunyai nilai mutlak yang lebih besar daripada yang lain dari barisan hadapan:

| 5 |> | 2 |

Begitu juga, pekali kedua baris kedua juga dominan secara serentak:

| -4 |> | 1 |

2- Pembolehubah x dan y jelas: 

X = (1 - 2y)/5

Y = x/4

3- Nilai sewenang-wenang awal diletakkan, dipanggil "benih": xo = 1, saya = 2.

4

Ia dapat melayani anda: anggaran mengikut selang waktu

X1 = (1 - 2 me)/5 = (1 - 2 × 2)/5 = -3/5 

Y1 = x1 / 4 = (-3/5) / 4 = -3/20 

5- Teruskan dengan cara yang sama untuk mendapatkan penghampiran kedua penyelesaian sistem persamaan:

X2 = (1 - 2 y1)/5 = (1 - 2x (-3/20))/5 = 13/50 

Y2 = x2/4 = (13/50)/4 = 13/200

6- Perubahan Ketiga:

X3 = (1 - 2 y2)/5 = (1 - 2 (13/200))/5 = 87/500

Y3 = x3/4 = (87/500)/4 = 87/2000

7- Keempat, sebagai lelaran akhir kes ilustrasi ini:

X4 = (1 - 2 y3)/5 = (1 - 2 (87/2000))/5 = 913/5000

Y4 = x4/4 = (913/5000)/4 = 913/20000

Nilai -nilai ini bertepatan dengan penyelesaian yang terdapat melalui kaedah penyelesaian lain. Pembaca boleh menyemaknya dengan cepat dengan bantuan program matematik dalam talian.

Analisis kaedah

Seperti yang dapat dilihat, dalam kaedah Gauss-Seidel, nilai anggaran yang diperolehi untuk pembolehubah sebelumnya dalam langkah yang sama mesti diganti dalam pemboleh ubah berikut. Ini membezakannya dari kaedah berulang lain seperti Jacobi, di mana setiap langkah memerlukan pendekatan ke peringkat sebelumnya. 

Kaedah Gauss-Seidel bukan prosedur selari, sementara Gauss-jordan. Ini juga sebab kaedah Gauss-Seidel mempunyai langkah-langkah yang kurang konvergensi-daripada kaedah Jordan.

Bagi keadaan matriks yang dominan diagonal, ini tidak selalu berpuas hati. Walau bagaimanapun, dalam kebanyakan kes sudah cukup untuk menukar pangkat sistem asal untuk memenuhi syarat. Di samping itu, kaedah hampir selalu berkumpul, walaupun keadaan dominasi pepenjuru tidak dipenuhi.

Hasil sebelumnya, yang diperolehi oleh empat lelaran kaedah Gauss-Seidel, boleh ditulis dengan cara perpuluhan:

Boleh melayani anda: Berapa banyak paksi simetri?

X4 = 0.1826

Y4 = 0.04565

Penyelesaian yang tepat untuk sistem persamaan yang dibangkitkan adalah:

X = 2/11 = 0.1818

Y = 1/22 = 0.04545.

Jadi hanya dengan 4 lelaran hasil diperolehi dengan ketepatan seribu (0.001).

Rajah 1 menggambarkan bagaimana lelaran berturut -turut dengan cepat menumpu kepada penyelesaian yang tepat.

Aplikasi

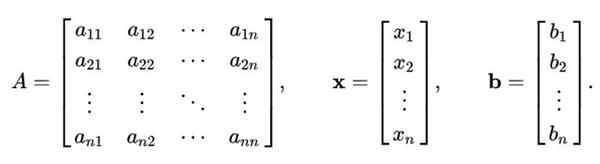
Kaedah Gauss-Seidel tidak terhad hanya kepada sistem persamaan linear 2 × 2. Prosedur di atas boleh digalakkan untuk menyelesaikan sistem linear n persamaan dengan n Tidak diketahui, yang diwakili matriks seperti ini:

Ke X = b

Di mana Ke Ia adalah matriks n x n, manakala X Ia adalah komponen vektor n pembolehubah yang akan dikira; dan b Ia adalah vektor yang mengandungi nilai istilah bebas.

Untuk merumuskan urutan lelaran yang digunakan dalam kes ilustrasi kepada sistem n x n, yang ingin mengira pembolehubah Xi, Formula berikut akan dikenakan:

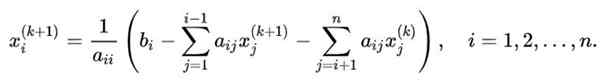
Dalam persamaan ini:

- k Ia adalah indeks untuk nilai yang diperolehi dalam lelaran k.

-K+1 Menunjukkan nilai baru dalam perkara berikut.

Jumlah lelaran akhir ditentukan apabila nilai yang diperolehi dalam lelaran K+1 berbeza dari yang diperoleh dengan segera sebelum ini, dalam jumlah ε yang tepatnya ketepatan yang dikehendaki.

Contoh kaedah Gauss-Seidel

- Contoh 1

Tulis algoritma umum yang membolehkan anda mengira vektor penyelesaian anggaran X sistem linear persamaan NXN, memandangkan matriks pekali Ke, Vektor istilah bebas b, Bilangan lelaran (iter) dan awal atau "benih" vektor X.

Penyelesaian

Algoritma terdiri daripada dua "untuk" kitaran, satu untuk bilangan lelaran dan yang lain untuk bilangan pembolehubah. Ia akan menjadi seperti berikut:

Untuk k ∊ [1 ... iter]

Untuk saya ∊ [1 ... n]

X [i]: = (1/a [i, i])*(b [i] - ΣJ = 1n(A [i, j]*x [j]) + a [i, i]*x [i])

Boleh melayani anda: notasi perpuluhan

- Contoh 2

Semak operasi algoritma sebelumnya dengan memohon perisian matematik Smath Studio percuma dan percuma, tersedia untuk Windows dan Android. Ambil sebagai contoh kes matriks 2 × 2 yang melayani kita untuk menggambarkan kaedah Gauss-Seidel.

Penyelesaian

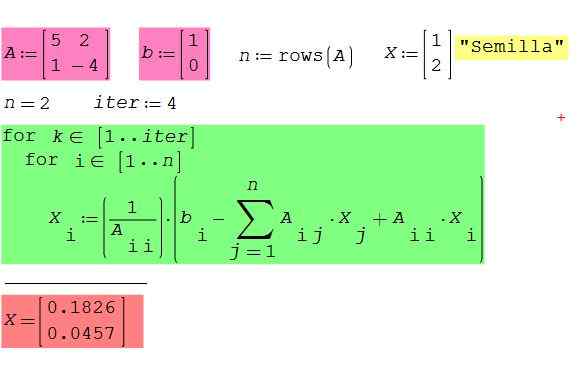Rajah 2. Sistem Persamaan Contoh 2 x 2, menggunakan perisian Smath Studio. Sumber: f. Zapata.

- Contoh 3

Sapukan algoritma Gauss-Seidel untuk sistem persamaan 3 × 3 berikut, yang sebelum ini telah diperintahkan sedemikian baris yang sama):

9 x1 + 2 x2 - x3 = -2

7 x1 + 8 x2 + 5 x3 = 3

3 x1 + 4 x2 - 10 x3 = 6

Gunakan vektor null sebagai benih dan pertimbangkan lima lelaran. Komen mengenai hasilnya.

Penyelesaian

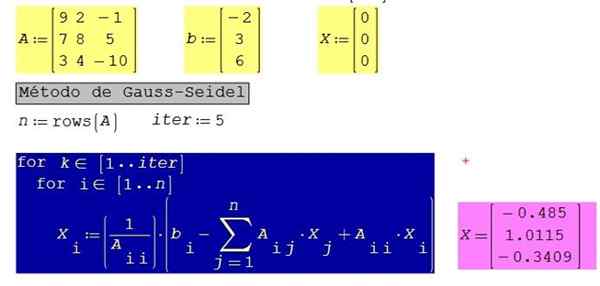Rajah 3. Penyelesaian sistem persamaan Contoh 3 yang diselesaikan, menggunakan Smath Studio. Sumber: f. Zapata.

Untuk sistem yang sama dengan 10 lelaran dan bukannya 5 hasil berikut diperolehi: x1 = -0.485; X2 = 1.0123; X3 = -0.3406

Ini menunjukkan bahawa ia sudah cukup dengan lima lelaran untuk mendapatkan tiga perpuluhan ketepatan dan kaedah itu dengan cepat menyampaikan kepada penyelesaiannya.

- Contoh 4

Dengan cara algoritma Gauss-Seidel yang diberikan, cari penyelesaian sistem persamaan 4 × 4 yang berlaku di bawah:

10 x1 - x2 + 2 x3 + 0 x4 = 6

-1 x1 + 11 x2 - 1 x3 + 3 x4 = 25

2 x1 - 1 x2 + 10 x3 - 1 x4 = -11

0 x1 + 3 x2 - 1 x3 + 8 x4 = 15

Untuk memulakan kaedah, gunakan benih ini:

x1 = 0, x2 = 0, x3 = 0 dan x4 = 0

Pertimbangkan 10 lelaran dan anggaran kesilapan hasilnya, membandingkan dengan lelaran nombor 11.

Penyelesaian

Rajah 4. Penyelesaian Sistem Persamaan Contoh 4, Menggunakan Smath Studio. Sumber: f. Zapata.

Apabila membandingkan dengan lelaran berikut (nombor 11), hasilnya sama. Perbezaan terbesar antara kedua -dua lelaran adalah perintah 2 × 10-8, Yang bermaksud bahawa penyelesaian yang ditunjukkan mempunyai ketepatan sekurang -kurangnya tujuh perpuluhan.

Rujukan

  1. Kaedah penyelesaian iteratif. Gauss-Seidel. Pulih dari: cimat.mx
  2. Kaedah berangka. Gauss-Seidel. Pulih dari: ujian.Cua.UAM.mx
  3. Numerik: Kaedah Gauss-Seidel. Pulih dari: belajar di linea.Anda.Edu.co
  4. Wikipedia. Kaedah Gauss-Seidel. Diperoleh dari: dalam. Wikipedia.com
  5. Wikipedia. Kaedah Gauss-Seidel. Pulih dari: Adakah.Wikipedia.com