Contoh, Latihan Sudut Konjugasi Dalaman dan Luaran

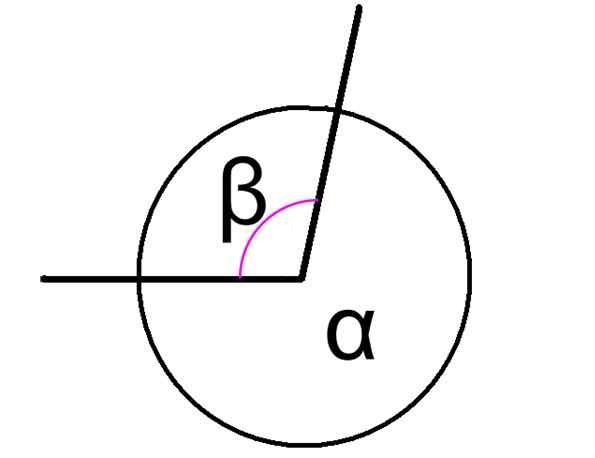
The Sudut konjugasi Mereka adalah yang ditambah hasil daripada 360 °, tanpa mengira sama ada sudut ini bersebelahan atau tidak. Rajah 1 menunjukkan dua sudut konjugasi, dilambangkan sebagai α dan β.

Dalam hal ini, sudut α dan β angka mempunyai puncak yang sama dan sisi mereka adalah perkara biasa, oleh itu mereka bersebelahan. Hubungan antara mereka dinyatakan seperti berikut:

α + β = 360º

Rajah 1. Dua sudut pusat konjugasi, jumlah. Sumber: Wikimedia Commons. Tiada pengarang yang boleh dibaca mesin yang disediakan. Thiago R Ramos diasumsikan (berdasarkan tuntutan hak cipta). [CC BY-SA 3.0 (http: // creativeCommons.Org/lesen/by-sa/3.0/)] ia adalah klasifikasi sudut dengan jumlahnya. Definisi penting lain termasuk sudut pelengkap, jumlahnya adalah 90 º dan Sudut Tambahan, yang berjumlah 180 º.

Sebaliknya, mari kita pertimbangkan dua garis selari yang dipotong oleh secant, yang pelupusannya ditunjukkan kemudian:

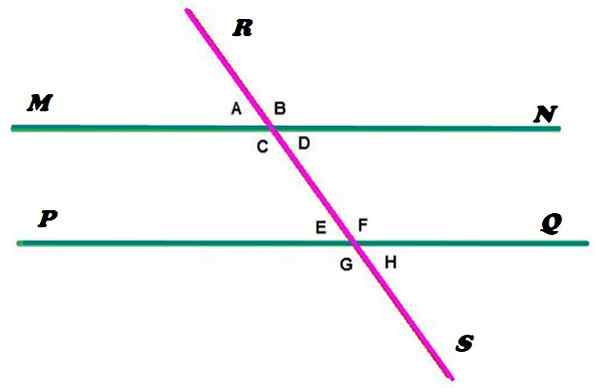
Rajah 2. Garis selari dipotong oleh secant. Sumber: f. Zapata.

Garis MN dan PQ selari, manakala garis RS mengeringkan, merentasi persamaan dalam dua mata. Seperti yang dapat dilihat, konfigurasi ini menentukan pembentukan 8 sudut, yang mana ia telah dilambangkan dengan huruf kecil.

Nah, menurut definisi yang diberikan pada mulanya, sudut A, B, C dan D dikonjugasi. Dan dengan cara yang sama mereka adalah E, F, G dan H, kerana kedua -dua kes dipenuhi:

A+B+C+D = 360º

Dan

E+F+G+H = 360º

Untuk konfigurasi ini, dua sudut konjugasi jika mereka berada di sisi yang sama berkenaan dengan garis pengeringan RS dan kedua -duanya adalah dalaman atau luaran. Dalam kes pertama terdapat perbincangan mengenai sudut Konjugasi dalaman, Semasa di tempat kedua, mereka adalah sudut konjugasi luaran.

[TOC]

Contoh

Dalam Rajah 2, sudut luaran adalah yang berada di luar rantau yang dibatasi oleh garisan Mn dan PQ, ia adalah sudut A, B, G dan H dan H. Walaupun sudut yang antara kedua -dua baris adalah C, D, E dan F dan F.

Boleh melayani anda: mata coplanares: persamaan, contoh dan latihan yang diselesaikan

Sekarang perlu menganalisis sudut mana yang ada di sebelah kiri dan di sebelah kanan Secant.

Di sebelah kiri RS adalah sudut A, C, E dan G. Dan di sebelah kanan adalah B, D, F dan H.

Kami segera meneruskan untuk menentukan pasangan sudut konjugasi, mengikut definisi yang diberikan dalam bahagian sebelumnya:

-A dan G, luaran dan ke kiri Rs.

-D dan f, dalaman dan di sebelah kanan Rs.

-B dan h, luaran dan di sebelah kanan Rs.

-C dan e, dalaman dan di sebelah kiri Rs.

Harta sudut konjugasi antara garis selari

Sudut konjugasi antara garis selari adalah tambahan, iaitu, jumlahnya sama dengan 180 °. Dengan cara ini, untuk Rajah 2, berikut dipenuhi:

A + G = 180º

D + F = 180º

B + H = 180º

C + E = 180º

Pasangan sudut yang sepadan untuk garis selari

Mereka adalah orang -orang yang berada di sisi yang sama dari garis pengeringan, mereka tidak bersebelahan dan salah satu daripadanya adalah dalaman dan yang lain adalah luaran. Adalah penting untuk memvisualisasikannya, kerana ukuran mereka adalah sama, kerana mereka bertentangan dengan sudut.

Kembali ke Rajah 2, sudut yang sepadan dikenalpasti sebagai:

-A dan e

-C dan g

-B dan f

-D dan h

Sudut dalaman segi empat segi

Quadrilaterals adalah poligon 4 -sided, termasuk dataran, segi empat tepat, trapeze, parallelogram dan rombus, sebagai contoh, sebagai contoh,. Tidak kira bentuknya, di mana -mana daripada mereka, ia dipenuhi bahawa jumlah sudut dalamannya adalah 360º, oleh itu mereka mematuhi definisi yang diberikan pada awalnya.

Mari kita lihat beberapa contoh kuadrilatur dan bagaimana mengira nilai sudut dalamannya mengikut maklumat bahagian sebelumnya:

Boleh melayani anda: Apakah 7 elemen lilitan?

Contoh

a) Tiga sudut ukuran kuadrilateral 75º, 110º dan 70º. Berapa banyak ukuran sudut yang selebihnya?

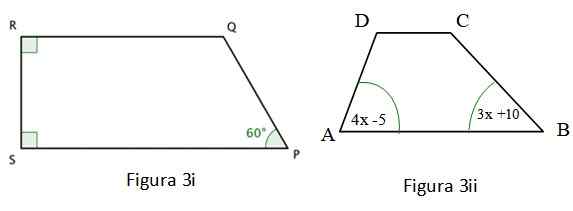
b) Cari nilai sudut ∠Q dalam Rajah 3 i.

c) Kirakan berapa banyak ukuran sudut ∠A Rajah 3 II.

Penyelesaian kepada

Biarkan α menjadi sudut yang hilang, ia dipenuhi bahawa:

α + 75 º + 110º + 70º = 360 → α = 105º

Penyelesaian b

Rajah 3i ditunjukkan adalah a Trapezoid Dan dua sudut dalamannya lurus, yang telah ditunjukkan dengan persegi warna di sudut. Untuk segiempat ini, berikut disahkan:

∠R + ∠S + ∠P + ∠Q = 360º; ∠S = ∠R = 90º; ∠P = 60º

Oleh itu:

∠ Q = 2 x 90º + 60º = 240º

Penyelesaian c

Quadrilateral Rajah 3 II juga merupakan trapeze, yang mana yang berikut dipenuhi:

∠A + ∠B + ∠C + ∠D = 360º

Oleh itu:

4x -5 + 3x + 10 +180 = 360

7x + 5 = 180

X = (180 - 5) / 7

x = 25

Untuk menentukan sudut yang diminta dalam pernyataan, ia digunakan bahawa ∠A = 4x - 5. Menggantikan nilai x yang sebelum ini dikira ia diikuti bahawa ∠A = (4 × 25) -5 = 95º

Latihan

- Latihan 1

Mengetahui bahawa salah satu sudut yang ditunjukkan bernilai 125, mencari ukuran 7 sudut yang tinggal dalam angka berikut dan membenarkan jawapannya.

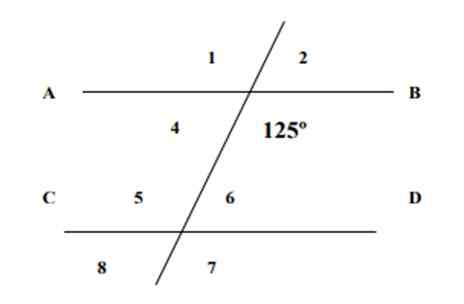Rajah 4. Garis dan sudut latihan 1. Sumber: f. Zapata.

Penyelesaian

Sudut 6 dan Sudut 125 adalah konjugasi dalaman, yang jumlahnya bernilai 180º, menurut harta sudut konjugasi, oleh itu:

∠6 + 125º = 180º → ∠6 = 180º - 125º = 55º

Sebaliknya ∠6 dan ∠8 adalah sudut bertentangan dengan puncak, yang ukurannya sama. Oleh itu ∠8 mengukur 55º.

Boleh melayani anda: aljabar vektor

Sudut ∠1 juga ditentang oleh puncak pada 125, maka kita dapat mengesahkan bahawa ∠1 = 125º. Kita juga boleh merayu kepada hakikat bahawa pasangan sudut yang sepadan mempunyai ukuran yang sama. Dalam angka sudut ini adalah:

∠7 = 125 °

∠2 = ∠6 = 55 °

∠1 = ∠5 = 125º

∠4 = ∠8 = 55 °

- Latihan 2

Cari nilai x dalam angka berikut dan nilai semua sudut:

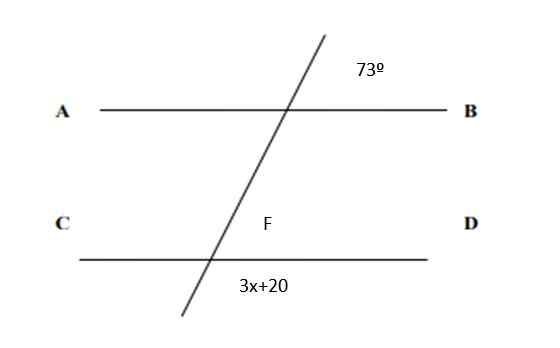Rajah 5. Garis dan sudut untuk latihan 2. Sumber: f. Zapata.

Penyelesaian

Oleh kerana mereka sepadan dengan pasangan, ia mengikuti bahawa f = 73º. Dan sebaliknya, jumlah pasangan konjugasi adalah 180º, oleh itu:

3x + 20º + 73º = 180º

3x = 180º - 73º -20º = 87

Akhirnya nilai x adalah:

x = 87/3 = 29

Bagi semua sudut, mereka muncul disenaraikan dalam angka berikut:

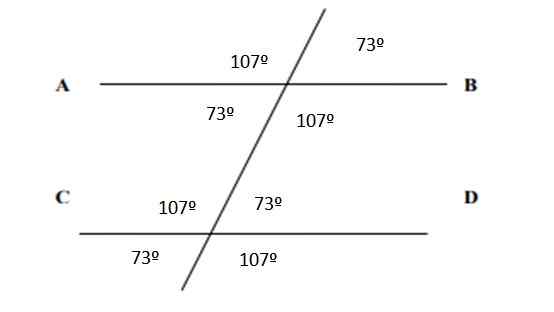Rajah 6. Sudut yang mengakibatkan Latihan 2. Sumber: f. Zapata.

Rujukan

1. Kumpulan sudut. Penjelasan sudut pelengkap, tambahan dan jelas. Pulih dari: ini.com/
2. Baldor, a. 1983. Geometri rata dan ruang dan trigonometri. Kumpulan tanah air budaya.
3. Corral, m. Matematik Libretxts: Sudut. Pulih dari: matematik.Libretxts.org.
4. Mathmania. Mengklasifikasikan dan membina sudut dengan pengukuran mereka. Pulih dari: Mathemania.com/
5. Wentworth, g. Geometri Planet. Pulih dari: gutenberg.org.
6. Wikipedia. Sudut konjugasi. Pulih dari: Adakah.Wikipedia.org.