Sudut Tambahan iaitu, Pengiraan, Contoh, Latihan

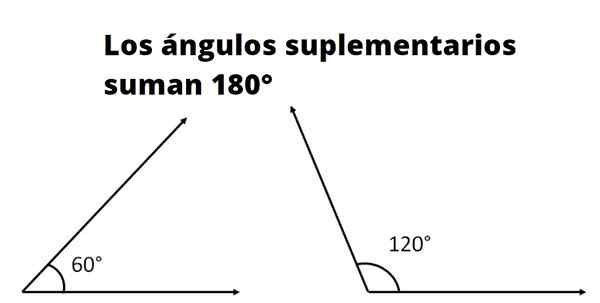
Dua atau lebih adalah Sudut Tambahan Sekiranya jumlah langkahnya sepadan dengan ukuran sudut rata. Ukuran sudut rata, juga dipanggil sudut rata, dalam darjah adalah 180º dan dalam radian adalah π.

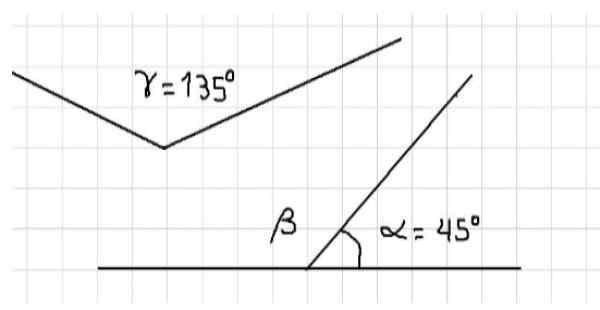
Sebagai contoh, kita mendapati bahawa tiga sudut dalaman segitiga adalah tambahan, kerana jumlah langkahnya adalah 180º. Tiga sudut ditunjukkan dalam Rajah 1. Dari yang di atas, α dan β adalah tambahan, kerana mereka bersebelahan dan jumlah penuh mereka sudut rata.

Rajah 1: α dan β adalah tambahan. α dan γ adalah tambahan. Sumber: f. Zapata.

Juga dalam angka yang sama, terdapat sudut α dan γ yang juga tambahan, kerana jumlah langkah mereka adalah sama dengan sejauh mana sudut rata, iaitu 180º. Tidak boleh dikatakan bahawa sudut β dan γ adalah tambahan kerana kedua -dua bodoh sudut langkah mereka lebih besar daripada 90º dan oleh itu jumlahnya melebihi 180º.

Sumber: Lafer.com

Sebaliknya, boleh dikatakan bahawa ukuran sudut β adalah sama dengan ukuran sudut γ, kerana jika β adalah tambahan α dan γ adalah tambahan α, maka β = γ = 135º.

[TOC]

Contoh

Dalam contoh berikut, diminta untuk mencari sudut yang tidak diketahui, yang ditunjukkan dengan soal siasat dalam Rajah 2. Mereka terdiri daripada contoh yang paling mudah untuk beberapa lebih rumit daripada pembaca harus lebih berhati -hati.

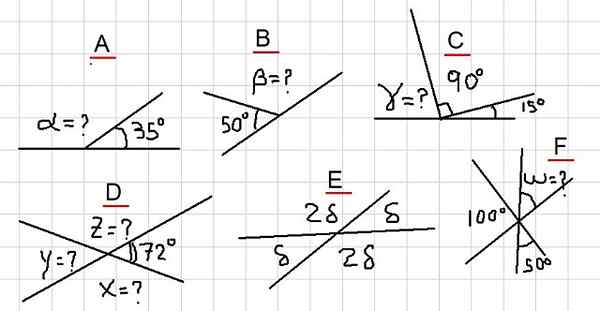Rajah 2. Pelbagai contoh sudut tambahan. Sumber: f. Zapata.

Contoh a

Dalam angka kita mempunyai sudut bersebelahan α dan 35º tambah sudut rata. Iaitu, α + 35º = 180º dan oleh itu ia dipenuhi bahawa: α = 180º- 35º = 145º.

Contoh b

Sebagai β adalah tambahan dengan sudut 50º, maka diikuti bahawa β = 180º - 50º = 130º.

Boleh melayani anda: apakah unsur -unsur perumpamaan? (Bahagian)

Contoh c

Dari Rajah 2C jumlah berikut diperhatikan: γ + 90º + 15º = 180º. Iaitu, γ adalah tambahan dengan sudut 105º = 90º + 15º. Disimpulkan kemudian: 

γ = 180º- 105º = 75º

Contoh d

Sebagai x adalah tambahan dengan 72º, ia mengikuti bahawa x = 180º - 72º = 108º. Di samping itu dan ia adalah tambahan dengan x, kemudian y = 180º - 108º = 72º.

Dan akhirnya z adalah tambahan dengan 72º, oleh itu z = 180º - 72º = 108º.

Contoh e

Sudut δ dan 2δ adalah tambahan, oleh itu δ + 2Δ = 180º. Yang bermaksud bahawa 3Δ = 180º, dan ini seterusnya membolehkan penulisan: δ = 180º / 3 = 60º.

Contoh f

Sekiranya kita memanggil sudut antara 100º dan 50º, maka perlu ditambah kepada mereka, kerana diperhatikan bahawa jumlah penuh mereka sudut rata.

Ia mengikuti bahawa u = 150º. Kerana anda ditentang oleh puncak ke w, maka w = u = 150º.

Latihan

Tiga latihan dicadangkan di bawah, di mana mereka nilai sudut a dan b mesti dijumpai dalam darjah, sehingga hubungan yang ditunjukkan dalam Rajah 3 dipenuhi. Konsep sudut tambahan digunakan dalam resolusi semuanya.

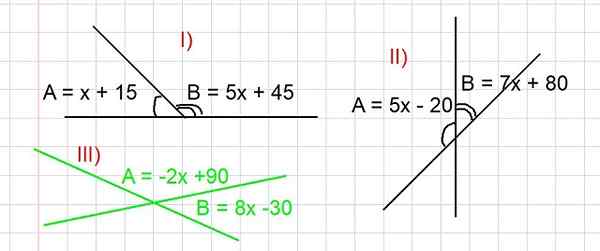Rajah 3. Rajah untuk menyelesaikan Latihan I, II dan III pada Sudut Tambahan. Semua sudut dinyatakan dalam darjah. Sumber: f. Zapata.

- Latihan I

Tentukan nilai sudut a dan b bahagian I) Rajah 3.

Penyelesaian

A dan B adalah tambahan, di mana A + B = 180 darjah perlu diganti, maka ungkapan A dan B digantikan sebagai fungsi x, seperti yang terdapat dalam imej:

(x + 15) + (5x + 45) = 180

Persamaan linear pertama diperoleh. Untuk menyelesaikannya, istilah dibuang: istilah:

6 x + 60 = 180

Boleh melayani anda: Nombor sebenar: sejarah, contoh, sifat, operasi

Membahagikan kedua -dua ahli antara 6 adalah:

x + 10 = 30

Dan akhirnya penjelasan, ia mengikuti bahawa x bernilai 20º.

Sekarang nilai x mesti diganti untuk mencari sudut yang diperintahkan. Dari situ anda perlu sudut a adalah: a = 20 +15 = 35º.

Dan bagi bahagiannya, sudut B ialah B = 5*20 + 45 = 145º.

- Latihan II

Cari nilai sudut a dan b bahagian II) Rajah 3.

Penyelesaian

Oleh kerana A dan B adalah sudut tambahan, A + B = 180 darjah mempunyai. Menggantikan ungkapan A dan B sebagai fungsi x yang diberikan dalam Bahagian II) Rajah 3 adalah:

(-2x + 90) + (8x - 30) = 180

Sekali lagi persamaan ijazah pertama diperolehi, yang mana syarat -syarat mestilah berkumpulan dengan mudah:

6 x + 60 = 180

Membahagikan kedua -dua ahli antara 6 adalah:

x + 10 = 30

Di mana ia mengikuti bahawa x bernilai 20º.

Iaitu sudut a = -2*20 + 90 = 50 °. Sementara sudut b = 8*20-30 = 130.

- Latihan III

Tentukan nilai sudut a dan b bahagian III) Rajah 3 (dalam hijau).

Penyelesaian

Oleh kerana A dan B adalah sudut tambahan, A + B = 180 darjah mempunyai. Ekspresi A dan B mesti diganti sebagai fungsi x yang diberikan dalam Rajah 3, yang anda miliki:

(5x - 20) + (7x + 80) = 180

12 x + 60 = 180

Membahagikan kedua -dua ahli dengan 12 untuk membersihkan nilai x, anda mempunyai:

x + 5 = 15

Akhirnya didapati bahawa x bernilai 10 darjah.

Sekarang teruskan untuk menggantikan untuk mencari sudut a: a = 5*10 -20 = 30 °. Dan untuk sudut b: b = 7*10 + 80 = 150º

Boleh melayani anda: berapakah julat statistik? (Dengan contoh)

Sudut tambahan dalam dua persamaan dipotong oleh secant

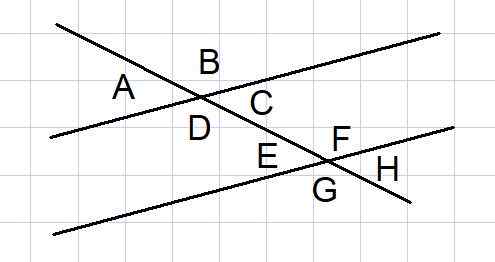Rajah 4. Sudut antara dua persamaan dipotong oleh secant. Sumber: f. Zapata.

Dua garisan selari yang dipotong oleh secant adalah pembinaan geometri biasa dalam beberapa masalah. Antara garis sedemikian, 8 sudut dibentuk seperti yang ditunjukkan dalam Rajah 4.

Daripada 8 sudut itu, beberapa pasang sudut adalah tambahan, yang kami senaraikan di bawah:

1. Sudut luaran ke dan b, dan eksterior g dan h
2. Sudut pedalaman d dan c, dan bahagian dalaman e dan f
3. Sudut luaran A dan G, dan B dan H luaran
4. Sudut dalaman D dan E, dan penghuni C dan F

Dengan kesempurnaan, sudut yang sama juga dinamakan:

1. Penggantian dalaman: d = f dan c = e
2. Penggantian luaran: a = h dan b = g
3. Yang sepadan: a = e dan c = h
4. Yang bertentangan dengan puncak a = c dan e = h
5. Yang sepadan: b = f dan d = g
6. Yang bertentangan dengan puncak b = d dan f = g

- Latihan iv

Merujuk kepada Rajah 4, di mana sudut menunjukkan antara dua garis selari yang dipotong oleh secant, tentukan nilai semua sudut dalam radian, mengetahui bahawa sudut a = π/6 radians.

Penyelesaian

A dan B adalah sudut luaran tambahan oleh itu b = π - a = π - π/6 = 5π/6

A = E = C = H = π/6

B = F = D = G = 5π/6

Rujukan

1. Baldor, j. Ke. 1973.Geometri rata dan ruang. Kebudayaan Amerika Tengah. 
2. Undang -undang dan formula matematik. Sistem pengukuran sudut. Diperolehi dari: Ingemecanica.com.
3. Wentworth, g. Geometri Planet. Pulih dari: gutenberg.org.
4. Wikipedia. Sudut Tambahan. Pulih dari: Adakah.Wikipedia.com
5. Wikipedia. Penghantar. Pulih dari: Adakah.Wikipedia.com
6. Zapata f. Goniometer: Sejarah, Bahagian, Operasi. Diperolehi dari: Lifer.com