Sifat nombor kompleks, contoh, operasi

The nombor kompleks Mereka adalah set berangka yang meliputi nombor sebenar dan semua akar polinomial, termasuk akar bahkan nombor negatif. Akar ini tidak wujud dalam set nombor sebenar, tetapi dalam nombor kompleks adalah penyelesaiannya.

Bilangan kompleks terdiri daripada bahagian sebenar dan yang lain disebut "khayalan". Bahagian sebenar dipanggil ke, Contohnya, dan bahagian khayalan Ib, dengan ke dan b nombor sebenar dan "saya" seperti Unit khayalan. Dengan cara ini nombor kompleks mengambil bentuk:

Z = a + ib

Rajah 1.- Perwakilan binomial nombor yang kompleks dari segi bahagian sebenar dan bahagian khayalan. Sumber: Pixabay.

Contoh nombor kompleks ialah 2 - 3i, -πi, 1 + (1/2) i. Tetapi sebelum beroperasi dengan mereka, mari kita lihat di mana unit khayalan berasal dari Yo, Memandangkan persamaan kuadrat ini:

x² - 10x + 34 = 0

Di mana a = 1, b = -10 dan c = 34.

Apabila formula pelarut digunakan untuk menentukan penyelesaian, kami dapati yang berikut:

Cara menentukan nilai √-36? Tidak ada nombor nyata yang persegi adalah jumlah negatif. Maka disimpulkan bahawa persamaan ini tidak mempunyai penyelesaian yang nyata.

Walau bagaimanapun, kita boleh menulis ini:

√-36 = √-6² = √6² (-1) = 6√-1

Sekiranya kita menentukan nilai tertentu x seperti itu:

x² = -1

Jadi:

x = ± √ 1

Dan persamaan sebelumnya akan mempunyai penyelesaian. Oleh itu, unit khayalan ditakrifkan sebagai:

I = √-1

Dan juga:

√-36 = 6i

Ramai ahli matematik zaman dahulu bekerja untuk menyelesaikan masalah yang sama, menonjolkan Renaissance Girolamo Cardano (1501-1576), Nicolo Fontana (1501-1557) dan Raffaele Bombelli (1526-1572).

Tahun kemudian René Descartes (1596-1650) dipanggil "khayalan" kepada kuantiti seperti √-36 contohnya. Atas sebab ini, √-1 dikenali sebagai Unit khayalan.

[TOC]

Sifat nombor kompleks

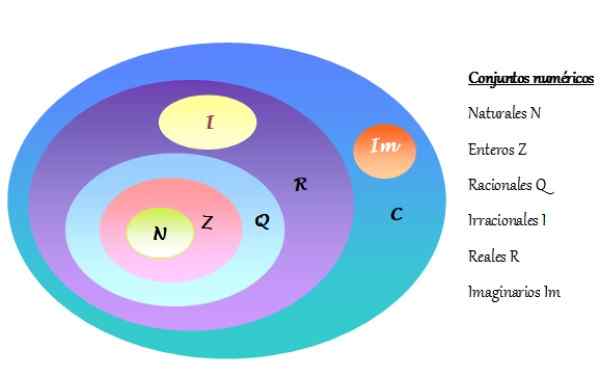
-Set nombor kompleks dilambangkan sebagai c dan termasuk nombor sebenar r dan nombor khayalan im. Set berangka diwakili dalam rajah Venn, seperti yang ditunjukkan dalam angka berikut:

Boleh melayani anda: Latihan pemfaktoran yang diselesaikan Rajah 2. Venn Diagram set berangka. Sumber: f. Zapata.

-Setiap nombor kompleks terdiri daripada satu bahagian sebenar dan bahagian khayalan yang lain.

-Apabila bahagian khayalan nombor kompleks adalah 0, ia adalah nombor sebenar yang murni.

-Sekiranya bahagian sebenar nombor kompleks adalah 0, maka nombornya adalah khayalan murni.

-Dua nombor kompleks adalah sama jika bahagian sebenar dan bahagian khayalan masing -masing adalah sama.

-Dengan bilangan kompleks, operasi yang diketahui, penolakan, pendaraban, produk dan pemberdayaan dijalankan, mengakibatkan bilangan lain yang kompleks.

Perwakilan nombor kompleks

Nombor kompleks dapat diwakili dengan pelbagai cara. Berikut adalah yang utama:

- Bentuk binomik

Ia adalah borang yang diberikan pada mulanya, di mana z adalah nombor kompleks, ke adalah bahagian sebenar, b adalah bahagian khayalan dan Yo Ia adalah unit khayalan:

Z = a + ib

Atau juga:

Z = x + iy

Salah satu cara untuk menggambarkan nombor kompleks adalah melalui satah kompleks yang ditunjukkan dalam angka ini. Paksi khayalan adalah menegak, manakala paksi sebenar adalah mendatar dan menandakan sebagai semula.

Nombor kompleks z Ia diwakili dalam pesawat ini sebagai titik koordinat (X, y) Sama ada (A, b), Seperti yang dilakukan dengan titik pesawat sebenar.

Jarak dari asal ke titik z adalah modul nombor kompleks, dilambangkan sebagai r, manakala φ adalah sudut yang membentuk r Dengan paksi sebenar.

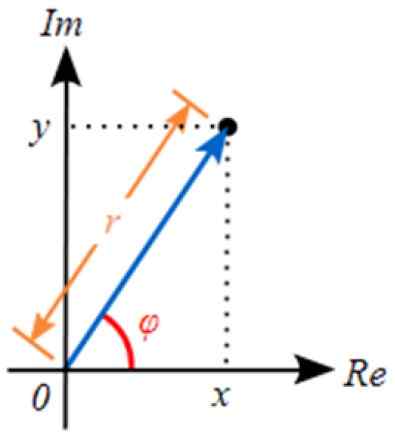
Rajah 3. Perwakilan nombor kompleks dalam satah kompleks. Sumber: Wikimedia Commons.

Perwakilan ini berkait rapat dengan vektor dalam pesawat sebenar. Nilai r sepadan dengan modul nombor kompleks.

Ia boleh melayani anda: Kaedah Gauss-Seidel: Penjelasan, Aplikasi, Contoh

- Bentuk kutub

Bentuk kutub terdiri daripada menyatakan jumlah kompleks yang memberikan nilai r dan dari φ. Sekiranya kita melihat angka, nilai r Ia sepadan dengan hipotenus segitiga yang betul. Kategori bernilai ke dan b, Wahai x dan dan.

Dalam bentuk binomial atau binomial, kita boleh beralih ke bentuk kutub oleh:

R = √x²+dan²

Sudut φ Ia adalah yang membentuk segmen r dengan paksi mendatar atau paksi khayalan. Ia dikenali sebagai argumen nombor kompleks. Cara ini:

φ = arctg (y/x)

Hujah mempunyai nilai tak terhingga, dengan mengambil kira bahawa setiap kali pulangan bertukar, yang bernilai 2π radian, r sekali lagi menduduki kedudukan yang sama. Dengan cara ini secara umum, argumen Z, yang dilambangkan arg (z), dinyatakan seperti berikut:

Arg (z) = φ + 2kπ

Di mana k adalah keseluruhan dan berfungsi untuk menunjukkan jumlah giliran bertukar: 2, 3, 4 .. . Tanda menunjukkan makna putaran, jika masa atau antihorario dibuat.

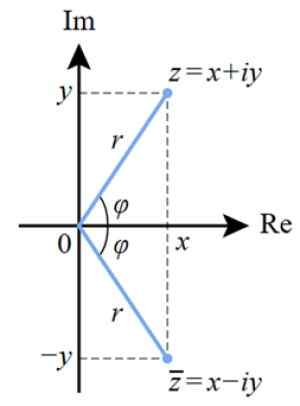
Rajah 4. Perwakilan kutub nombor kompleks dalam satah kompleks. Sumber: Wikimedia Commons.

Dan jika kita mahu lulus bentuk kutub ke bentuk binomial, kita menggunakan alasan trigonometri. Dari angka sebelumnya kita dapat melihatnya:

x = r cos φ

y = r sen φ

Dengan cara ini z = r (cos φ+i sin φ)

Yang disingkat seperti ini:

z = r cis φ

Contoh nombor kompleks

Nombor kompleks berikut diberikan binomial:

a) 3 + i

b) 4

d) -6i

Dan ini dalam tork yang teratur:

a) (-5, -3)

b) (0, 9)

c) (7.0)

Akhirnya, kumpulan ini diberi kutub atau trigonometri:

a) √2 cis 45º

b) √3 cis 30º

Boleh melayani anda: Pengedaran Hypergeometric: Formula, Persamaan, Model

c) 2 cis 315º

Apa yang mereka buat?

Kegunaan nombor kompleks melampaui resolusi persamaan darjah kedua yang ditunjukkan pada mulanya, kerana ia penting dalam bidang kejuruteraan dan fizik, terutama dalam:

-Kajian gelombang elektromagnetik

-Analisis arus dan voltan alternatif

-Pemodelan semua jenis isyarat

-Teori relativiti, di mana masa dianggap sebagai magnitud khayalan.

Operasi dengan nombor kompleks

Dengan nombor kompleks kita dapat melaksanakan semua operasi yang dilakukan dengan sebenar. Ada yang lebih mudah dilakukan jika angka -angka itu datang secara binomi, seperti jumlah dan penolakan. Sebaliknya, pendaraban dan pembahagian lebih mudah jika mereka dijalankan dengan bentuk kutub.

Mari lihat beberapa contoh:

- Contoh 1

Tambah z₁ = 2 + 5i dan z₂ = -3 -8i

Penyelesaian

Bahagian sebenar ditambah secara berasingan dari bahagian khayalan:

z₁ + z₂ = (2 + 5i) + (-3 -8i) = -1 -3i

- Contoh 2

Multiply z₁ = 4 cis 45º dan z₂ = 5 cis 120º

Penyelesaian

Ia dapat ditunjukkan bahawa produk dua nombor kompleks dalam kutub atau trigonometri diberikan oleh:

z₁ . z₂ = r₁.r₂ Cis (φ₁ + φ₂)

Menurut Ini:

z₁ . z₂ = (4 × 5) cis (45 + 120) = 20 cis 165º

Permohonan

Aplikasi mudah nombor kompleks adalah untuk mencari semua akar persamaan polinomial seperti yang ditunjukkan pada permulaan artikel.

Dalam kes persamaan x² - 10x + 34 = 0, apabila memohon formula pelarut ia diperolehi:

Oleh itu penyelesaiannya adalah:

x₁ = 5 + 3i

x₂ = 5 - 3i

Rujukan

1. Earl, r. Nombor kompleks. Pulih dari: matematik.lembu.Ac.UK.
2. Figuera, j. 2000. Matematik 1st. Dipelbagaikan. Edisi bersama.
3. Hoffmann, j. 2005. Pemilihan masalah matematik. Penerbitan Monfort.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Wikipedia. Nombor kompleks. Diperoleh dari: dalam.Wikipedia.org