Nombor Perdana, Contoh, Latihan Ciri

The Nombor Perdana, juga dipanggil sepupu mutlak, adalah nombor semula jadi yang hanya boleh dibahagikan antara satu sama lain dan 1. Dalam kategori ini, nombor seperti: 2, 3, 5, 7, 11, 13, 17, 19, 23 dan banyak lagi yang datang dalam kategori ini.

Sebaliknya, nombor kompaun boleh dibahagikan dengan sendirinya, dengan 1 dan sekurang -kurangnya satu lagi nombor. Kami mempunyai contoh pada 12, yang boleh dibahagikan dengan 1, 2, 4, 6 dan 12. Oleh konvensyen, 1 tidak termasuk dalam senarai nombor perdana atau dalam sebatian.

Rajah 1. Beberapa nombor utama. Sumber: Wikimedia Commons.

Pengetahuan mengenai nombor perdana bermula dari masa jauh; Orang Mesir kuno sudah mengendalikan mereka dan pasti diketahui lama dahulu.

Nombor ini sangat penting, kerana mana -mana bilangan semula jadi boleh diwakili oleh produk nombor perdana, sebagai perwakilan unik ini, kecuali dalam urutan faktor.

Fakta ini ditubuhkan sepenuhnya dalam teorem yang dipanggil Teorem asas aritmetik, yang menyatakan bahawa nombor yang bukan sepupu semestinya terdiri daripada produk nombor.

[TOC]

Ciri -ciri nombor perdana

Di bawah ciri -ciri utama nombor utama:

-Mereka tidak terhingga, kerana namun besar nombor perdana selalu dapat dijumpai.

-Sekiranya nombor Perdana p tidak membahagikan tepat ke nombor lain ke, Kemudian dikatakan bahawa p dan ke Mereka sepupu antara satu sama lain. Apabila ini berlaku, satu -satunya pembahagi biasa ialah 1.

Tidak perlu ke Menjadi sepupu mutlak. Sebagai contoh, 5 adalah sepupu, dan walaupun 12 tidak, kedua -dua nombor adalah sepupu antara satu sama lain, kerana kedua -duanya mempunyai pembahagi biasa hingga 1.

-Apabila nombor Perdana p bahagikan kekuatan nombor n, Ia juga membahagikan a n. Pertimbangkan 100, yang merupakan kuasa 10, khususnya 10². Ia berlaku bahawa 2 membahagikan kedua -dua 100 dan 10.

-Semua nombor Perdana adalah ganjil kecuali 2, oleh itu digit terakhir mereka ialah 1, 3, 7 atau 9. 5 tidak termasuk, kerana walaupun ia adalah ganjil dan sepupu, ia tidak pernah menjadi angka terakhir nombor perdana yang lain. Malah semua nombor yang berakhir dalam 5 adalah gandaan ini dan oleh itu bukan sepupu.

Boleh melayani anda: simetri pusat: sifat, contoh dan latihan

-Yeah p Ia adalah sepupu dan pembahagi produk dua nombor ke.b, Jadi p Bahagikan salah satu daripada mereka. Contohnya, Nombor Perdana 3 membahagikan produk 9 x 11 = 99, kerana 3 adalah pembahagi 9.

Bagaimana untuk mengetahui sama ada nombor sepupu

The Primal Itu adalah nama yang diberikan kepada kualiti sepupu. Baik, matematik Perancis Teorem kecil Fermat, Yang mengatakan demikian:

"Diberi nombor semulajadi sepupu p dan nombor semula jadi ke lebih besar daripada 0, ia dipenuhi ke^p - ke Ia adalah pelbagai p, selagi p menjadi sepupu ".

Kita dapat menyokong ini menggunakan nombor kecil, contohnya anggaplah P = 4, bahawa kita sudah tahu bahawa ia bukan sepupu dan a = 6:

6⁴ - 6 = 1296 - 6 = 1290

Nombor 1290 tidak betul -betul dibahagikan antara 4, oleh itu 4 bukan nombor utama.

Mari buat ujian sekarang dengan p = 5, iaitu sepupu dan a = 6:

6⁵ - 6 = 7766 - 6 = 7760

7760 boleh dibahagikan antara 5, kerana mana -mana nombor yang berakhir pada 0 atau 5 adalah. Sebenarnya 7760/5 = 1554. Oleh kerana teorem kecil Fermat dipenuhi, kita dapat memastikan bahawa 5 adalah nombor utama.

Ujian melalui teorem adalah berkesan dan langsung dengan bilangan kecil, di mana operasi itu mudah dilakukan, tetapi apa yang perlu dilakukan jika mereka meminta kami untuk mengetahui primal yang besar?

Dalam hal ini, bilangannya berturut -turut dibahagikan antara semua nombor perdana kecil, sehingga beberapa pembahagian yang tepat atau bahawa kota kurang dari pembahagi.

Sekiranya ada bahagian yang tepat, ini bermakna nombor itu adalah kompaun dan jika kuota kurang daripada pembahagi, ini bermakna nombor itu sepupu. Kami akan mengamalkannya pada tahun diselesaikan 2.

Cara Mencari Nombor Perdana

Terdapat nombor perdana yang tidak terhingga dan tidak ada formula unik untuk menentukannya. Walau bagaimanapun, memerhatikan beberapa nombor perdana seperti ini:

Boleh melayani anda: sudut null: definisi dan ciri, contoh, latihan

3, 7, 31, 127 ..

Diperhatikan bahawa mereka berada dalam Borang 2ⁿ - 1, dengan n = 2, 3, 5, 7, 9 ... kami memberi jaminan kepada anda:

2² - 1 = 4 - 1 = 3; 2³ - 1 = 8 - 1 = 7; 2⁵ - 1 = 32 - 1 = 31; 2⁷ - 1 = 128 - 1 = 127

Tetapi kita tidak dapat memastikan bahawa secara umum 2ⁿ - 1 Jadilah sepupu, kerana terdapat beberapa nilai n yang mana ia tidak berfungsi, contohnya pada 4:

2⁴ - 1 = 16 - 1 = 15

Dan nombor 15 bukan sepupu, kerana ia berakhir pada 5. Walau bagaimanapun, salah satu nombor perdana terbesar yang diketahui, yang dijumpai oleh pengiraan komputer -buatan, berada dalam Borang 2ⁿ - 1 dengan:

N = 57.885.161

The Formula Mersenne memberi jaminan kepada kami bahawa 2^p - 1 selalu sepupu, selagi p Jadilah sepupu juga. Sebagai contoh, 31 adalah sepupu, jadi pasti bahawa 2³¹ - 1 Ia juga:

2³¹ - 1 = 2.147.483.647

Walau bagaimanapun, formula itu hanya membenarkan beberapa nombor utama ditentukan, tidak semua.

Formula Euler

Polinomial berikut membolehkan mencari nombor perdana selagi n adalah antara 0 dan 39:

P (n) = n² + N + 41

Kemudian, di bahagian Latihan yang diselesaikan terdapat contoh penggunaannya.

Pemeriksaan Eratostenes

Eratóstenes adalah fizikal dan matematik Yunani kuno yang hidup pada abad ketiga hingga.C. Dia mencipta kaedah grafik untuk mencari nombor utama yang boleh kita amalkan dengan bilangan kecil, ia dipanggil skrin Eratóstenes (skrin seperti penapis).

-Nombor diletakkan dalam jadual seperti yang ditunjukkan dalam animasi.

-Maka nombor juga dilabel, kecuali yang kita tahu adalah sepupu. Semua yang lain adalah gandaan ini dan oleh itu mereka bukan sepupu.

-Gandaan 3, 5, 7 dan 11 juga ditandakan, tidak termasuk mereka semua kerana kita tahu mereka adalah sepupu.

-Gandaan 4, 6, 8, 9 dan 10 telah ditandakan, kerana mereka adalah sebatian dan oleh itu gandaan mana -mana sepupu yang ditunjukkan.

Boleh melayani anda: Sejarah Trigonometri dari Asalnya

-Akhirnya, bilangan baki tidak ditandakan adalah sepupu.

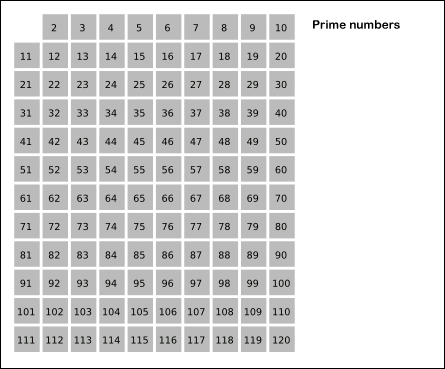Rajah 2. Animasi Pemeriksaan Eratostenes. Sumber: Wikimedia Commons.

Latihan

- Latihan 1

Menggunakan polinomial Euler untuk nombor perdana, cari 3 nombor lebih besar daripada 100.

Penyelesaian

Ini adalah polinomial yang dicadangkan untuk mencari nombor utama, yang beroperasi untuk nilai n antara 0 dan 39.

P (n) = n² + N + 41

Melalui Tanteo kita memilih nilai n, contohnya n = 8:

P (8) = 8² + 8 + 41 = 113

Sebagai n = 8 menghasilkan nombor perdana lebih besar daripada 100, maka kita menilai polinomial untuk n = 9 dan n = 10:

P (9) = 9² + 9 + 41 = 131

P (10) = 10² + 10 + 41 = 151

- Latihan 2

Ketahui sama ada nombor berikut adalah sepupu:

a) 13

b) 191

Penyelesaian kepada

13 cukup kecil untuk menggunakan teorem kecil Fermat dan bantuan kalkulator.

Kami menggunakan A = 2 supaya nombor tidak terlalu besar, walaupun mereka juga boleh digunakan A = 3, 4 atau 5:

2¹³ - 2 = 8190

8190 boleh dibahagikan antara 2, kerana ia adalah walaupun 13 adalah sepupu. Pembaca boleh menyokongnya dengan melakukan ujian yang sama dengan A = 3.

Penyelesaian b

191 sangat besar untuk mencuba teorem dan kalkulator biasa, tetapi kita boleh tote pembahagian antara setiap nombor perdana. Kami menghilangkan untuk membahagikan 2 kerana 191 tidak bahkan dan bahagian itu tidak tepat atau nisbah kurang dari 2.

Kami cuba membahagikan 3:

191/3 = 63,666 ..

Dan ia tidak memberi tepat, ataupun kuota kurang daripada pembahagi (63,666 ... lebih besar daripada 3)

Kami terus menguji 191 oleh sepupu 5, 7, 11, 13 dan bahagian yang tepat tidak dicapai, atau nisbah kurang daripada pembahagi. Sehingga ia membahagikan antara 17:

191/17 = 11, 2352 ..

Kerana ia tidak tepat dan 11,2352 ... ia kurang daripada 17, nombor 191 adalah sepupu.

Rujukan

1. Baldor, a. 1986. Aritmetik. Edisi dan Pengagihan Edisi Codex.
2. Prieto, c. Nombor Primo. Diperoleh dari: Halaman.Matem.Unam.mx.
3. Sifat nombor perdana. Pulih dari: mae.Ufl.Edu.
4. Smartick. Nombor Primo: Cara Mencari Mereka Dengan Penapis Eratostenes. Pulih dari: Smartick.adalah.
5. Wikipedia. nombor perdana. Pulih dari: Adakah.Wikipedia.org.