Matematik

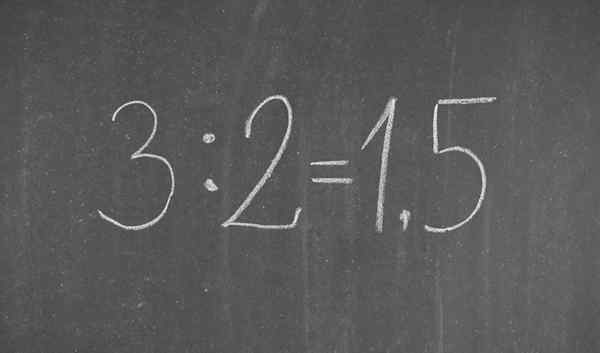
Notasi perpuluhan

Notasi perpuluhan
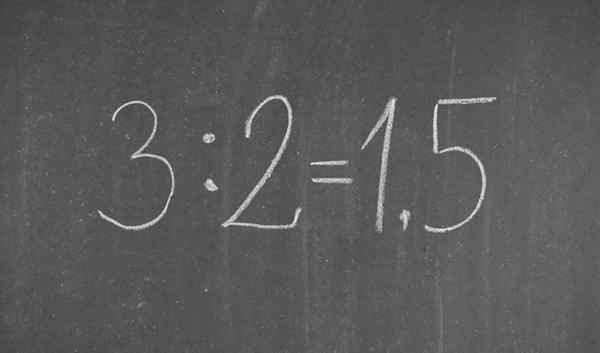Pecahan 3/2 yang ditulis dalam notasi perpuluhan

Apa itu notasi perpuluhan?

The notasi perpuluhan Ia terdiri daripada menulis nombor sebenar melalui seluruh bahagian dan bahagian perpuluhan, kedua -duanya dipisahkan oleh satu titik atau koma. Seluruh bahagian tersisa dan bahagian perpuluhan di sebelah kanan titik itu.

0 boleh muncul di seluruh bahagian dan dalam perpuluhan. Sebagai contoh, angka berikut adalah nombor perpuluhan:

  • 0.25
  • 1.5903
  • 4,19367

Perhatikan bahawa bahagian perpuluhan nombor ini adalah terhingga, tetapi terdapat juga angka dengan bahagian perpuluhan yang tidak terhingga, seperti 0.333333 ..., di mana titik -titik yang menggembirakan diletakkan sebagai cara untuk menunjukkan bahawa bilangan perpuluhan berterusan selama -lamanya selama -lamanya.

Secara umum, nombor perpuluhan terhingga boleh ditulis sebagai:

N.ke1ke2ke3... ken

Menjadi n integer dan n jumlah perpuluhan, sementara perpuluhan tak terhingga mengamalkan bentuk:

N.ke1ke2ke3…

Dalam perpuluhan 0.25 dikenal pasti:

  • N = 0
  • ke1 = 2
  • ke2 = 5

Perpuluhan timbul sebagai cara lain untuk menyatakan nombor rasional, yang berbentuk atau patah. Malah, pecahan apa pun boleh ditulis dalam notasi perpuluhan, seperti yang akan dilihat dengan segera.

Mereka juga berfungsi untuk mewakili nombor yang tidak berasal dari pecahan, nombor tidak rasional, seperti: π, √2, √3, √5, nombor "e" dan banyak lagi.

Contoh nombor perpuluhan

Nombor perpuluhan boleh didapati dari pecahan dengan cara yang sangat mudah: mengira kuota pengangka antara penyebut. Jika penyebutnya adalah unit yang diikuti oleh sifar, ini sangat mudah:

  • 8/10 = 0.8
  • - (5/100) = -0.05

Dalam kes pertama, sebagai penyebut adalah 10, titik perpuluhan diletakkan segera ke kiri 8 dan perpuluhan 0.8 Membaca "8 Kesepuluh" atau "Zero Point Eight".

Dalam kes kedua, kerana penyebutnya adalah 100, anda perlu meletakkan titik perpuluhan dua tempat di sebelah kiri 5, dan kerana bilangannya negatif, ia berbunyi "kurang 5 ratus" atau "kurang sifar titik lima".

Apabila penyebut bukan unit diikuti oleh 0, bahagian panjang digunakan:

Perhatikan bahawa untuk melaksanakan bahagian ini, kerana pengangka kurang daripada penyebut, ia telah didarabkan terlebih dahulu dengan 10 dan dengan berbuat demikian, 0 diikuti oleh titik perpuluhan dalam kuota, supaya tidak mengubah operasi, sehingga tidak untuk mengubah operasi. Kemudian teruskan secara normal untuk membahagikan 10 hingga 2 yang sama dengan 5 dan sisa bahagian adalah 0.

Boleh melayani anda: Jumlah vektor

Bentuk perpuluhan pecahan ½ adalah 0.5, bahawa "Zero Point Five" dibaca:

Pecahan 7/8 adalah contoh lain. Kerana 7 kurang daripada 8, ia melipatgandakan 7 × 10 = 70, 0 diletakkan di dalam kota diikuti oleh titik perpuluhan dan biasanya dibahagikan:

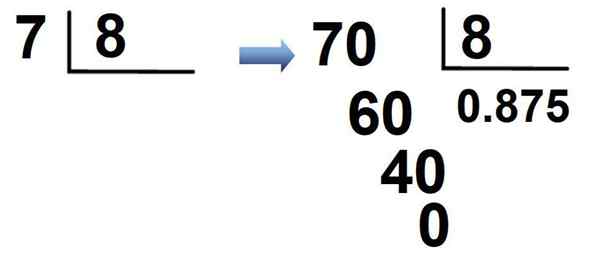
Hasilnya ialah pecahan ditulis dalam notasi perpuluhan sebagai:

7/8 = 0.875

Nombor ini, seperti hasil sebelumnya, adalah perpuluhan terhingga dan cara membacanya ialah: "Zero Point Lapan Ratus Tujuh Puluh -Five". Melalui prosedur ini, pecahan berikut juga ditulis dalam notasi perpuluhan:

8/10 = 0.8

5/7 = 0.714285714 ..

9/20 = 0.Empat lima

3/8 = 0.375

Perhatikan bahawa seperti dalam semua pecahan ini pengangka kurang daripada penyebut, seluruh bahagian perpuluhan yang dihasilkan adalah 0. Walau bagaimanapun, nombor bercampur atau a Pecahan yang tidak betul (Yang pengangka yang lebih besar daripada penyebutnya) juga mempunyai perwakilan perpuluhan.

Dalam kes ini, seluruh bahagian lebih besar daripada atau sama dengan 1 jika pecahan positif, dan kurang daripada -1 jika ia negatif:

9/4 = 2.25

10/3 = 3.333333 ..

-12/5 = -2.4

1 ½ = 1.5

2 ¾ = 2.75

Bahagian keseluruhan dan bahagian pecahan perpuluhan negatif

Dalam contoh -contoh sebelumnya, diperhatikan bahawa untuk mencari ekspresi perpuluhan pecahan, pengangka dan penyebut hanya dibahagikan. Walaupun pecahannya negatif, hanya tanda tolak yang dimasukkan ke dalam ungkapan decimient yang setara.

Walau bagaimanapun, seluruh bahagian dan bahagian pecahan perpuluhan berbeza mengikut tanda yang anda bawa.

Apabila perpuluhan positif, seperti 2.25, seluruh bahagiannya adalah 2 dan bahagian perpuluhannya ialah 0.25 dan nombor boleh ditulis sebagai jumlah keseluruhan bahagian dan bahagian perpuluhan, seperti ini:

2.25 = 2 + 0.25

Seluruh bahagian ditakrifkan sebagai integer dengan lebih rendah daripada perpuluhan dan bahagian perpuluhan selalu positif. Untuk 2.25, integer yang lebih rendah adalah 2.

Tetapi dalam kes pecahan -12/5, bersamaan dengan perpuluhan -2.4 perkara di atas tidak berfungsi.

Boleh melayani anda: Apakah bahagian pesawat Cartesian?

 Jika -2 ia adalah seluruh bahagian, dan 0.4 Bahagian perpuluhan, dengan menambah akan diperoleh:

-2 + 0.4 = -1.6 ≠ -2.4

Oleh itu, seluruh bahagian -2.4 tidak boleh -2 tetapi integer yang lebih rendah: -3. Tetapi dalam kes itu, bahagian pecahan tidak akan menjadi 0.4, kerana dengan menambah:

-3 + 0.4 = -2.6 ≠ -2.4

Jadi apakah bahagian perpuluhan nombor negatif -2.4? Ia mengurangkan nombor perpuluhan dari seluruh bahagiannya dan hasilnya akan sentiasa positif:

-2.4 - ( - 3) = 0.6

Akhirnya, terbukti dengan menambahkan seluruh bahagian dan bahagian pecahan, perpuluhan yang dicari diperoleh:

-3 + 0.6 = -2.4

Prosedur untuk mencari bahagian keseluruhan dan perpuluhan dari mana -mana nombor, tanpa mengira tanda itu, diringkaskan dengan cara ini:

  • Seluruh bahagian adalah integer yang lebih rendah daripada nombor perpuluhan.
  • Bahagian perpuluhan dikira dengan menolak perpuluhan dari seluruh bahagiannya.

Walau bagaimanapun, untuk tujuan pengiraan praktikal, nombor perpuluhan -2.4 boleh dipecahkan sebagai - (2 + 0.4) = - 24/10 atau:

Seperti yang dapat dilihat, perwakilan notasi perpuluhan nombor tidak unik.

Jenis perpuluhan

Terdapat nombor perpuluhan yang bahagian perpuluhannya adalah terhingga atau tidak terhingga, yang digunakan sebagai kriteria klasifikasi:

Perpuluhan yang terhingga atau tepat

Apabila perpuluhan terhingga, seperti 0.125, ia juga mengatakan bahawa mereka perpuluhan yang tepat.

Perpuluhan tak terhingga

Perpuluhan tak terhingga diperoleh apabila sisa pembahagian antara pengangka dan penyebut tidak pernah dibuat 0.

Dengan syarat bahawa perpuluhan berasal dari kuota antara dua bilangan bulat, bahagian perpuluhan ini berkala, iaitu, ia terdiri daripada satu atau beberapa angka yang diulangi selama -lamanya, yang dipanggil tempoh.

Contohnya, nombor 3.333333 ... berasal dari pecahan yang tidak wajar 10/3, ia adalah perpuluhan berkala: seluruh bahagian adalah 3, dan selepas titik perpuluhan, nombor 3 diulangi selama -lamanya. Ini boleh dilambangkan dengan meletakkan lengkung atau topi pada nombor yang diulang:

Tempoh ini boleh menjadi angka yang lebih besar, seperti dalam pecahan 5/7, yang perwakilan dalam notasi perpuluhan adalah 0.71428571428571428 ... dan ditulis sebagai:

Boleh melayani anda: variasi berkadar

Perpuluhan ini di mana tempoh itu muncul sejurus selepas titik perpuluhan dipanggil Perpuluhan berkala tulen. Walau bagaimanapun, dalam perkara ini:

Tempoh, iaitu 45, didahului oleh dua digit yang tidak diulang lagi di bahagian perpuluhan: 23. Angka ini dipanggil ante-tempoh, kerana ia mendahului tempoh. Dalam kes ini ia adalah Perpuluhan akhbar campuran.

Akhirnya ada perpuluhan tak terhingga yang bukan akhbar, yang tidak berasal dari kuota antara dua nombor keseluruhan. Seperti yang disebutkan pada mulanya, perpuluhan ini tergolong dalam keseluruhannya nombor tidak rasional, Seperti nombor pi, contohnya.

Latihan yang diselesaikan

Latihan 1

Tulis berangka nombor perpuluhan berikut:

a) sifar titik empat ratus empat puluh
b) Lima ribu
c) Dua unit dan lima ratus
d) Tiga titik dua puluh orang negatif
e) satu titik lapan ratus dua puluh ribu lima ratus enam puluh tiga

  • Penyelesaian

a) 0.447

b) 0.005

c) 2.05

d) -3.27

e) 1.824563

Latihan 2

Klasifikasi nombor perpuluhan berikut dalam perpuluhan tepat, akhbar murni, surat khabar campuran atau nombor yang tidak rasional. Dalam semua kes, nyatakan nilai seluruh bahagian, dan jika mereka adalah akhbar atau akhbar bercampur, juga menunjukkan nilai tempoh dan anterior, yang sesuai:

a) 0.35627

b) 1.21212121 ..

c) -1.32

d) 1.414213562 ... = √2

  • Penyelesaian

a) 35627 adalah perpuluhan yang tepat. Seluruh bahagiannya adalah 0 dan bahagian perpuluhannya adalah 0.35627.

b) 1.21212121 ... adalah akhbar perpuluhan yang tidak terhingga dan tulen, seluruh bahagian adalah 1 dan tempohnya 21.

c) -1.32 adalah perpuluhan yang tepat dan negatif, yang seluruhnya adalah -2. Bahagian perpuluhan dikira dengan menolak nombor perpuluhan dari seluruh bahagian:

-1.32 - (-2) = 0.68

d) Ekspresi perpuluhan √2 adalah tak terhingga dan tidak berkala, kerana ia adalah nombor yang tidak rasional.

Ia adalah akhbar bercampur, seluruh bahagiannya adalah 3, anterior adalah 1 dan tempoh 89.

Rujukan

  1. Sumbangan pedagogi dan bahan didaktik. Notasi perpuluhan. Pulih dari: tecdigital.TEC.Ac.Cr.
  2. Baldor, a. 2007. Aritmetik teoritis praktikal. Kumpulan editorial patria s.Ke. daripada c.V.
  3. Matematik untuk perdagangan. Memahami notasi perpuluhan. Diperolehi dari: OpenTextBC.Ac.
  4. Unam. Nombor rasional: makna dan perwakilan. Pulih dari: redi.Kodik.Unam.mx.