Papomudas

Apa itu papomudas?

Dia Papomudas Ini adalah prosedur untuk menyelesaikan ekspresi algebra. Akronimnya menunjukkan susunan keutamaan operasi: tanda kurung, kuasa, pendaraban, pembahagian, penambahan dan penolakan. Menggunakan perkataan ini, anda dapat dengan mudah mengingati urutan di mana ungkapan yang terdiri daripada beberapa operasi mesti diselesaikan.

Umumnya, dalam ungkapan berangka anda dapat menemui beberapa operasi aritmetik bersama -sama, seperti jumlah, penolakan, pendaraban dan bahagian, yang juga boleh menjadi pecahan, kuasa dan akar. Untuk menyelesaikannya, perlu mengikuti prosedur yang menjamin bahawa hasilnya betul.

Ekspresi aritmetik yang terdiri daripada gabungan operasi ini mesti diselesaikan mengikut keutamaan perintah, yang juga dikenali sebagai hierarki operasi, yang ditubuhkan lama dahulu dalam konvensyen sejagat. Oleh itu, semua orang dapat mengikuti prosedur yang sama dan memperoleh hasil yang sama.

Ciri -ciri

Papomudas adalah prosedur standard yang menetapkan perintah yang mesti diikuti apabila ungkapan mesti diberikan, yang terdiri daripada gabungan operasi seperti jumlah penolakan, pendaraban dan pembahagian.

Prosedur ini menetapkan perintah keutamaan operasi berhubung dengan yang lain pada masa mereka akan menjadi; iaitu, setiap operasi mempunyai peralihan atau tahap hierarki yang dapat diselesaikan.

Perintah di mana operasi yang berbeza dari ekspresi mesti diselesaikan diberikan oleh setiap akronim kata papomudas. Dengan cara ini, anda mesti:

1. PA: kurungan, kurungan atau kunci persegi.
2. PO: Kuasa dan Akar.
3. MU: Pendaraban.
4. D: Bahagian.
5. J: Penambahan atau jumlah.
6. S: penolakan atau penolakan.

Prosedur ini juga dipanggil dalam bahasa Inggeris sebagai Pemdas; Dengan mudah ingat perkataan ini dikaitkan dengan frasa: "Tolong maafkan ibu saudara saya yang tersayang", Di mana setiap huruf awal sepadan dengan operasi aritmetik, dengan cara yang sama seperti papomudas.

Cara menyelesaikannya?

Berdasarkan hierarki yang ditubuhkan oleh papomudas untuk menyelesaikan operasi ekspresi, adalah perlu untuk memenuhi perintah berikut:

• Pertama, semua operasi yang berada dalam simbol kumpulan, seperti kurungan, kunci, kurungan dan bar pecahan mesti diselesaikan. Apabila terdapat simbol pengelompokkan di lain -lain, anda harus mula mengira dari dalam.

Boleh melayani anda: Kejayaan Kuadratik: Contoh, Peraturan dan Latihan Diselesaikan

Simbol -simbol ini digunakan untuk menukar susunan di mana operasi diselesaikan, kerana apa yang selalu ada di dalamnya mesti selalu diselesaikan.

• Kemudian kuasa dan akar diselesaikan.
• Di tempat ketiga, pendaraban dan bahagian diselesaikan. Ini mempunyai urutan keutamaan yang sama; Oleh itu, apabila kedua -dua operasi ini dijumpai dalam ungkapan, yang muncul terlebih dahulu mesti diselesaikan, membaca ungkapan dari kiri ke kanan.
• Akhirnya jumlah dan penolakan diselesaikan, yang juga mempunyai urutan keutamaan yang sama dan, oleh itu, ia diselesaikan yang muncul pertama dalam ungkapan, dibaca dari kiri ke kanan.
• Operasi tidak boleh dicampur apabila dibaca dari kiri ke kanan, anda mesti sentiasa mengikut urutan keutamaan atau hierarki yang ditubuhkan oleh papomudas.

Adalah penting untuk diingat bahawa hasil setiap operasi mesti diletakkan dalam urutan yang sama berhubung dengan orang lain, dan semua langkah pertengahan mesti dipisahkan dengan tanda sehingga mencapai hasil akhir.

Permohonan

Prosedur papomudas digunakan apabila anda mempunyai gabungan operasi yang berbeza. Mengambil kira bagaimana mereka diselesaikan, ini boleh digunakan dalam:

Ungkapan yang mengandungi jumlah dan penolakan

Ia adalah salah satu operasi yang paling mudah, kerana kedua -duanya mempunyai urutan keutamaan yang sama, supaya ia mesti diselesaikan bermula dari kiri ke kanan dalam ungkapan; Sebagai contoh:

22 -15 + 8 +6 = 21.

Ungkapan yang mengandungi jumlah, penolakan dan pendaraban

Dalam kes ini, operasi keutamaan tertinggi adalah pendaraban, maka jumlah dan penolakan diselesaikan (yang pertama dalam ungkapan). Sebagai contoh:

6 _* 4 - 10 + 8 _* 6 - 16 + 10 _* 6

= 24 -10 + 48 - 16 + 60

= 106.

Ungkapan yang mengandungi jumlah, pengurangan pendaraban dan pembahagian

Dalam kes ini terdapat gabungan semua operasi. Ia bermula dengan menyelesaikan pendaraban dan pembahagian yang mempunyai keutamaan yang lebih baik, maka jumlah dan pengurangan. Membaca ungkapan dari kiri ke kanan, ia diselesaikan mengikut hierarki dan kedudukannya dalam ungkapan; Sebagai contoh:

Boleh melayani anda: mumm

7 + 10 _* 13 - 8 + 40 ÷ 2

= 7 + 130 - 8 + 20

= 149.

Ungkapan yang mengandungi jumlah, penolakan, pendaraban, pembahagian dan kuasa

Dalam kes ini salah satu daripada angka itu dinaikkan kepada kuasa, yang dalam tahap keutamaan mesti diselesaikan terlebih dahulu, dan kemudian menyelesaikan pendaraban dan bahagian, dan akhirnya jumlah dan penolakan:

4 + 4² _* 12 - 5 + 90 ÷ 3

= 4 + 16 _* 12 - 5 + 90 ÷ 3

= 4 + 192 - 5 + 30

= 221.

Seperti kuasa, akar juga mempunyai urutan kedua keutamaan; Oleh itu, dalam ungkapan yang mengandungi mereka, mereka mesti terlebih dahulu diselesaikan daripada pendaraban, bahagian, jumlah dan penolakan:

5 _* 8 + 20 ÷ √16

= 5 _* 8 + 20 ÷ 4

= 40 + 5

= 45.

Ungkapan yang menggunakan simbol pengelompokan

Apabila tanda -tanda digunakan seperti tanda kurung, kunci, kurungan dan pecahan bar, yang ada di dalamnya diselesaikan terlebih dahulu, tanpa mengira perintah keutamaan operasi yang terkandung dalam hubungannya dengan orang -orang di luar ini, seolah -olah ia akan berurusan dengan berasingan ungkapan:

14 ÷ 2 - (8 - 5)

= 14 ÷ 2 - 3

= 7 - 3

= 4.

Sekiranya dalam ini terdapat beberapa operasi, ini mesti diselesaikan dengan urutan hierarki. Maka operasi lain yang membentuk ungkapan diselesaikan; Sebagai contoh:

2 + 9 * (5 + 2³ - 24 ÷ 6) - 1

= 2 + 9 * (5 + 8 - 4) - 1

= 2 + 9 * 9 - 1

= 2 + 81 - 1

= 82.

Dalam beberapa ungkapan, simbol pengelompokan di dalam yang lain digunakan, seperti ketika perlu mengubah tanda operasi. Dalam kes -kes tersebut, ia mesti bermula dengan menyelesaikan dari dalam ke luar; iaitu, memudahkan simbol pengumpulan yang berada di tengah -tengah ungkapan.

Umumnya, perintah untuk menyelesaikan operasi yang terkandung dalam simbol -simbol ini adalah: pertama menyelesaikan apa yang ada dalam kurungan (), kemudian kurungan [] dan akhirnya kunci .

90 - 3_*[12 + (5_*4) - (4_*2)]

= 90 - 3_* [12 + 20 - 8]

Boleh melayani anda: kebarangkalian teoritis: bagaimana untuk mengeluarkannya, contoh, latihan

= 90 - 3 _* 24

= 90 - 72

= 18.

Latihan

Latihan pertama

Cari nilai ungkapan berikut:

dua puluh² + √225 - 155 + 130.

Penyelesaian

Memohon papomudas, kuasa dan akar harus diselesaikan terlebih dahulu, dan kemudian menambah dan pengurangan. Dalam kes ini, dua operasi pertama tergolong dalam urutan yang sama, jadi yang pertama kali diselesaikan, bermula dari kiri ke kanan:

dua puluh² + √225 - 155 + 130

= 400 + 15 -155 + 130.

Kemudian tambah dan penolakan, bermula di sebelah kiri juga:

400 + 15 -155 + 130

= 390.

Latihan kedua

Cari nilai ungkapan berikut:

[- (6³ - 3⁶) ÷ (8 _* 6 ÷ 16)].

Penyelesaian

Ia bermula dengan menyelesaikan operasi yang berada di dalam kurungan, mengikuti perintah hierarki yang mereka miliki mengikut papomudas.

Pertama, kuasa kurungan pertama diselesaikan, maka operasi kurungan kedua diselesaikan. Memandangkan mereka tergolong dalam susunan yang sama, operasi pertama ungkapan diselesaikan:

[- (6³ - 3⁶) ÷ (8 _* 6 ÷ 16)]

= [- (216-729) ÷ (8 _* 6 ÷ 16)]

= [ - (216 - 729) ÷ (48 ÷ 16)]

= [- (-513) ÷ (3)].

Sebagai operasi dalam kurungan telah diselesaikan, kini pembahagian yang mempunyai hierarki terbesar diteruskan:

[- (-513) ÷ (3)] = [- (-171)]]].

Akhir. Oleh itu, hasil ungkapan adalah:

[- (-171)] = 171.

Latihan ketiga

Cari nilai ungkapan berikut:

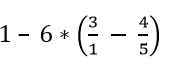
Penyelesaian

Pecahan yang ada dalam kurungan diselesaikan:

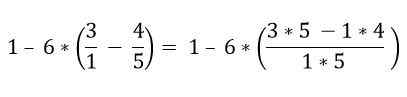
Dalam kurungan ada beberapa operasi. Pendaraban pertama kali diselesaikan dan kemudian penolakan; Dalam kes ini, bar pecahan dianggap sebagai simbol kumpulan dan bukan sebagai pembahagian, jadi operasi bahagian atas dan bawah mesti diselesaikan:

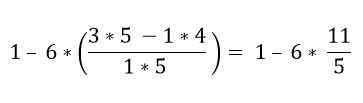
Dengan perintah hierarki, pendaraban mesti diselesaikan:

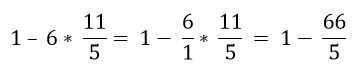
Akhirnya, penolakan diselesaikan: