Parallelepiped

Parallelepipeds adalah angka geometri enam, di mana bertentangan selari antara satu sama lain. Contoh: bata, kotak kasut, baldi, dll.

Apa itu selari?

A parallelepiped Ia adalah badan geometri yang dibentuk oleh enam wajah, yang ciri utamanya adalah bahawa semua wajahnya adalah selaras dan juga wajah yang bertentangan selari antara satu sama lain. Ia adalah polyhedron biasa dalam kehidupan seharian kita, kerana kita dapat menemuinya dalam kotak kasut, bentuk bata, bentuk gelombang mikro, dll.

Menjadi polyhedron, paralelepiped mengandungi jumlah terhingga dan semua wajahnya rata. Ia adalah sebahagian daripada kumpulan prisma, yang merupakan polyhedra di mana semua simpangnya terkandung dalam dua pesawat selari.

Unsur -unsur parallelepiped

Muka

Mereka masing -masing kawasan yang dibentuk oleh selaras yang mengehadkan parallelepiped. Parallelepiped mempunyai enam muka, di mana setiap wajah mempunyai empat muka bersebelahan dan bertentangan. Di samping itu, setiap wajah selari dengan sebaliknya.

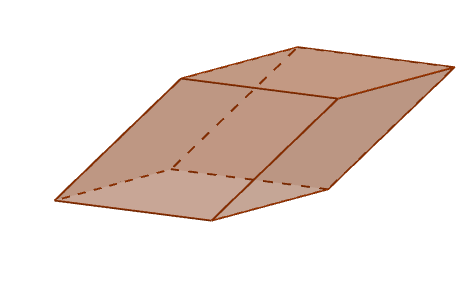Perspektif parallelepiped

Tepi

Mereka adalah bahagian biasa dua muka. Secara keseluruhan, paralelepiped mempunyai dua belas tepi.

Puncak

Ini adalah titik umum tiga muka yang bersebelahan dua hingga dua. Parallelepiped mempunyai lapan simpul.

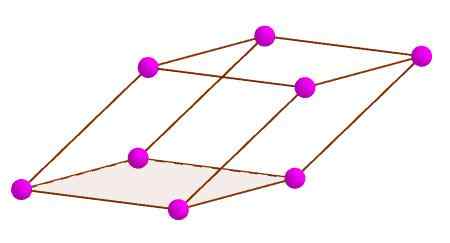Simpang selari

Pepenjuru

Memandangkan dua muka selari yang bertentangan antara satu sama lain, kita dapat melukis segmen garis yang pergi dari puncak satu muka ke puncak yang bertentangan.

Segmen ini dikenali sebagai pepenjuru paralelepip. Setiap parallelepiped mempunyai empat pepenjuru.

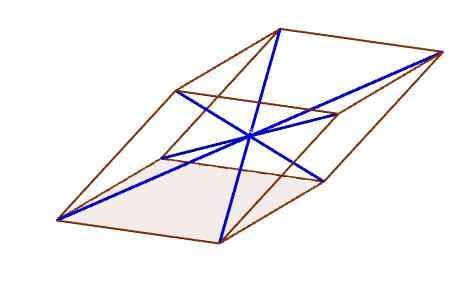Diagonals of a parallelepiped

Pusat

Ia adalah titik di mana semua pepenjuru bersilang.

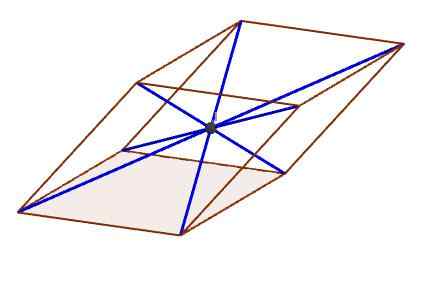Titik dalam angka menunjukkan pusat, di mana semua pepenjuru bersilang

Ciri -ciri parallelepiped

Seperti yang telah kita nyatakan, badan geometri ini mempunyai dua belas tepi, enam muka dan lapan titik.

Dalam parallelepiped, tiga set yang dibentuk oleh empat tepi dapat dikenalpasti, yang selari antara satu sama lain. Di samping itu, tepi set ini juga mematuhi harta yang mempunyai panjang yang sama.

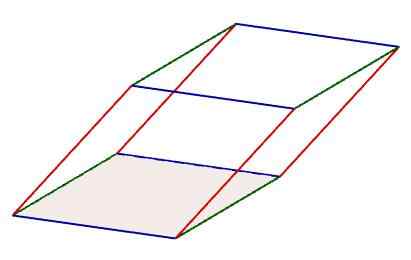Ciri -ciri parallelepiped

Harta lain yang ditimbulkan.

Di samping itu, parallelepipeds, sebagai polyhedros cembung, mematuhi teorem Euler untuk polyhedros, yang memberi kita hubungan antara bilangan muka, bilangan tepi dan bilangan simpang. Hubungan ini diberikan dalam bentuk persamaan berikut:

C + v = a + 2

Ciri ini dikenali sebagai ciri Euler. Di mana c adalah bilangan muka, dan bilangan simpang dan bilangan tepi.

Jenis Paralleepípedos

Kita boleh mengklasifikasikan parallelepípedos berdasarkan wajah mereka, pada jenis berikut:

Orthoedro

Mereka adalah parallelepípedos di mana wajah mereka terdiri daripada enam segi empat tepat. Setiap segi empat tepat berserenjang dengan mereka yang mana ia berkongsi kelebihan. Mereka adalah yang paling biasa dalam kehidupan seharian kita, ini menjadi bentuk biasa kasut dan kotak bata.

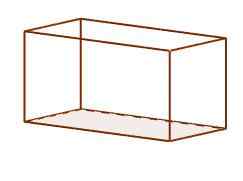Orthoedro parallelepiped

Kiub biasa atau hexaedro

Ini adalah kes tertentu yang sebelumnya, di mana setiap muka adalah persegi.

Boleh melayani anda: EllipseKiub biasa atau hexaedro

Kubus juga merupakan sebahagian daripada badan geometri yang dipanggil pepejal platonik. Pepejal platonik adalah polyhedron cembung, sehingga kedua -dua wajahnya dan sudut dalamannya sama antara satu sama lain.

Romboedro

Ia adalah parallelepiped yang mempunyai rhombus. Rhombus ini semuanya sama antara satu sama lain, kerana mereka berkongsi tepi.

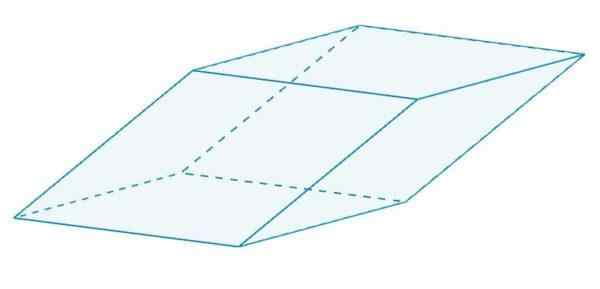A romboedro

Romboiedro

Enam wajahnya adalah rhomboid. Ingatlah bahawa rhomboid adalah poligon empat -sisi dan empat sudut yang sama dua hingga dua. Rhomboids adalah paralelogram yang tidak persegi, atau segi empat tepat, atau rhombus.

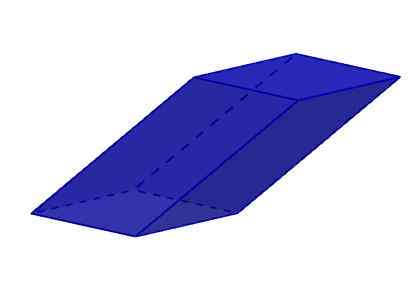Romboiedro

Sebaliknya, paralelepiped serong adalah yang sekurang -kurangnya satu ketinggian tidak sepadan dengan kelebihannya. Dalam klasifikasi ini kita boleh memasukkan rhomboedros dan rhomboiedros.

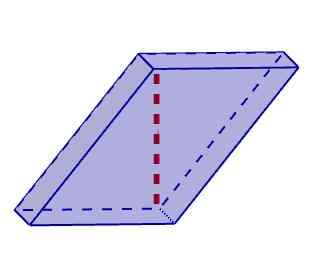Parallelepiped serong

Pengiraan pepenjuru

Untuk mengira pepenjuru orthoedro kita boleh menggunakan teorem pythagoras untuk r r³.

Ingatlah bahawa orthoedro mempunyai ciri -ciri bahawa setiap sisi berserenjang dengan sisi yang berkongsi kelebihan. Dari fakta ini kita dapat menyimpulkan bahawa setiap kelebihan berserenjang dengan mereka yang berkongsi puncak.

Untuk mengira panjang pepenjuru orthoedro, kami meneruskan seperti berikut:

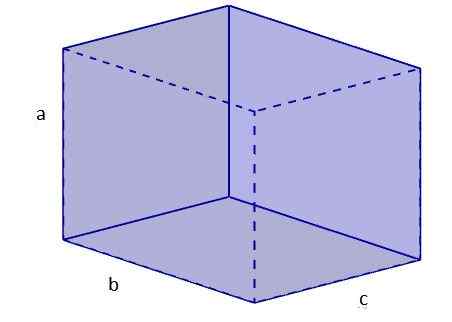
1. Kami mengira pepenjuru salah satu wajah, yang akan kami letakkan dengan asas. Untuk ini kita menggunakan teorem pythagoras. Mari namakan pepenjuru d_b.

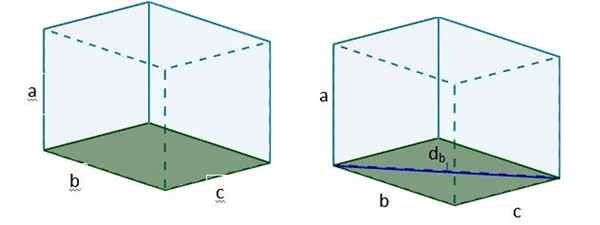
2. Kemudian dengan d_b Kita boleh membentuk segitiga segi empat tepat baru, sehingga hipotenus segitiga tersebut adalah pepenjuru yang dicari.

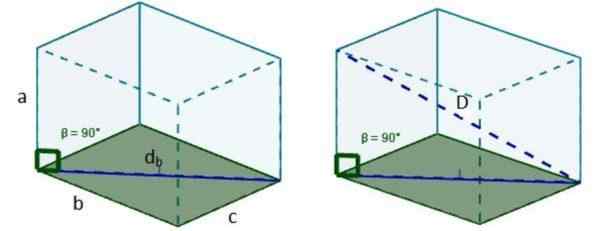
3. Kami menggunakan teorem Pythagoras sekali lagi dan kami mempunyai panjang pepenjuru itu:

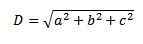
Cara lain untuk mengira pepenjuru dengan cara yang lebih grafik adalah dengan jumlah vektor percuma.

Ingatlah bahawa dua vektor percuma A dan B ditambah dengan meletakkan ekor vektor B dengan hujung vektor a.

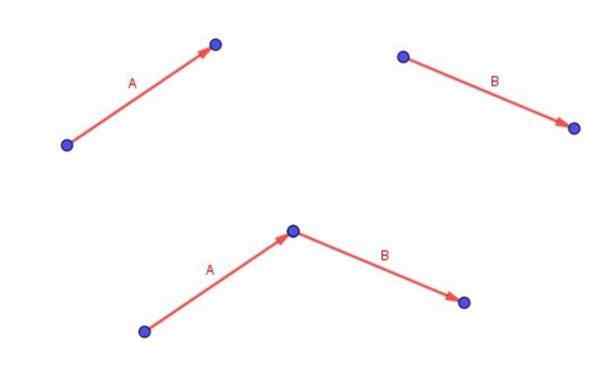
Vektor (a + b) adalah yang bermula di ekor a dan berakhir di hujung b.

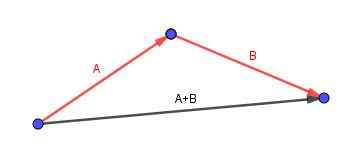
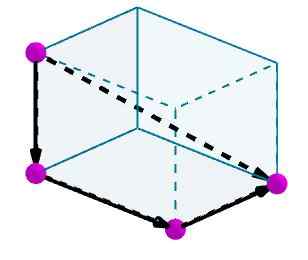
Pertimbangkan parallelepiped yang kita mahu mengira pepenjuru. Kami mengenal pasti tepi dengan vektor berorientasikan mudah.

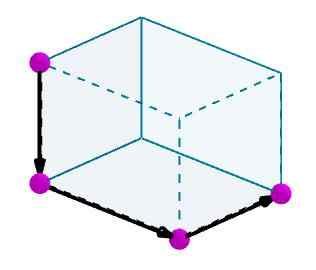
Kemudian kami menambah vektor ini dan vektor yang dihasilkan akan menjadi pepenjuru dari paralelepiped.

Kawasan selari

Kawasan paralelepiped diberikan oleh jumlah setiap kawasan wajahnya.

Sekiranya kita menentukan salah satu sisi sebagai pangkalan,

Ke_L + 2_B = Jumlah kawasan

Kemana_L Ia sama dengan jumlah kawasan di semua sisi bersebelahan dengan pangkalan, yang disebut kawasan sampingan dan ke_B Ia adalah kawasan asas.

Bergantung pada jenis parallelepiped yang kami bekerja, kami boleh menulis semula formula tersebut.

Kawasan orthoedro

Diberikan oleh formula

A = 2 (AB + BC + CA).

Contoh 1

Memandangkan orthoedro berikut, dengan sisi a = 6 cm, b = 8 cm dan c = 10 cm, hitung kawasan parallelepiped dan panjang pepenjurunya.

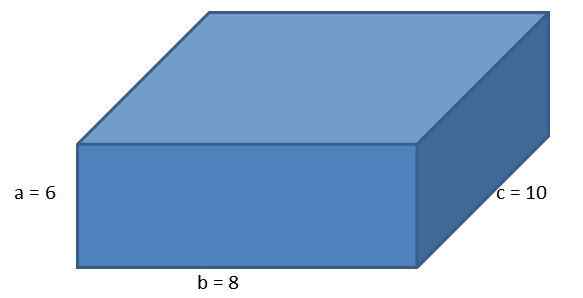
Menggunakan formula untuk kawasan orthoedro kita mesti

A = 2 [(6) (8) + (8) (10) + (10) (6)] = 2 [48 + 80 + 60] = 2 [188] = 376 cm².

Perhatikan bahawa sebagai orthoedro adalah panjang mana -mana empat pepenjuru adalah sama.

Ia boleh melayani anda: Integral Tidak Takdirkan: Hartanah, Aplikasi, Pengiraan (Contoh)

Menggunakan teorem pythagoras untuk ruang kita harus

D = (6² + 8² + 10²)^1/2 = (36 + 64 + 100)^1/2 = (200)^1/2

Kawasan kiub

Oleh kerana setiap kelebihan mempunyai panjang yang sama, kita mempunyai A = B dan A = C. Menggantikan formula sebelumnya yang kita ada

A = 2 (aa + aa + aa) = 2 (3a²) = 6a²

A = 6A²

Contoh 2

Kotak konsol permainan mempunyai bentuk kiub. Jika kita mahu membungkus kotak ini dengan kertas hadiah, berapa banyak kertas yang akan kita belanjakan untuk mengetahui bahawa panjang tepi kiub adalah 45 cm?

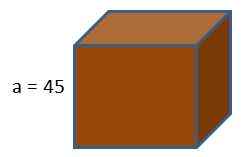
Menggunakan formula kawasan kiub kami mendapatnya

A = 6 (45 cm)² = 6 (2025 cm²) = 12150 cm²

Kawasan rhomboedro

Kerana semua wajahnya sama, sudah cukup untuk mengira kawasan salah satu daripada mereka dan membiaknya dengan enam.

Kami mempunyai kawasan rombus boleh dikira oleh pepenjuru dengan formula berikut

Ke_R = (Dd)/2

Menggunakan formula ini, ia mengikuti bahawa jumlah kawasan rhomboedro adalah

Ke_T = 6 (dd)/2 = 3dd.

Contoh 3

Wajah rhomboedro seterusnya dibentuk oleh rhombus yang pepenjuru adalah d = 7 cm dan d = 4 cm. Kawasan anda akan

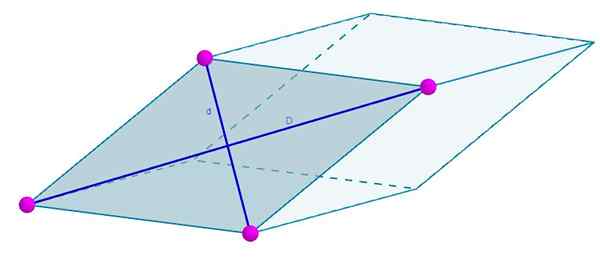
A = 3 (7 cm) (4 cm) = 84 cm².

Kawasan rhomboiedro

Untuk mengira kawasan rhomboiedro kita mesti mengira kawasan rhomboid yang mengarangnya. Oleh kerana paralelepipeds memenuhi harta yang bertentangan dengan kawasan yang sama, kita dapat mengaitkan sisi di tiga rakan sebaya.

Dengan cara ini kami mempunyai kawasan anda

Ke_T = 2b₁h₁ + 2b₂h₂ + 2b₃h₃

Di mana b_Yo adalah pangkalan yang dikaitkan dengan sisi dan h_Yo ketinggian relatifnya bersamaan dengan pangkalan tersebut.

Contoh 4

Pertimbangkan parallelepiped berikut,

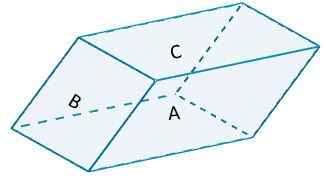
di mana sisi a dan sisi a '(sisi bertentangan mereka) berasaskan b = 10 dan setiap ketinggian h = 6. Kawasan yang ditandakan akan mempunyai nilai

Ke₁ = 2 (10) (6) = 120

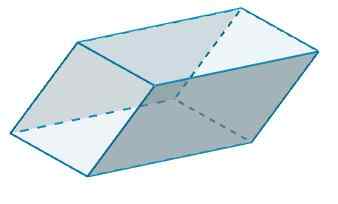
B dan b 'mempunyai b = 4 dan h = 6, maka

Ke₂ = 2 (4) (6) = 48

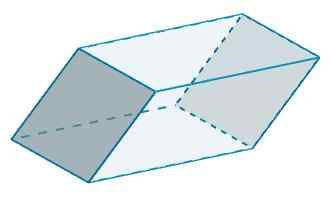
Dan c dan c 'mempunyai b = 10 dan h = 5, juga

Ke₃ = 2 (10) (5) = 100

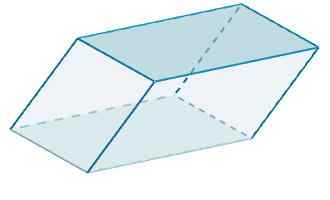
Akhirnya kawasan rhomboiedro adalah

A = 120 + 48 + 100 = 268.

Kelantangan parallelepiped

Formula yang memberi kita jumlah parallelepiped adalah hasil dari kawasan salah satu wajahnya kerana ketinggian yang sepadan dengan wajah tersebut.

V = a_Ch_C

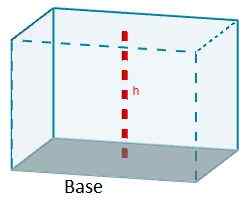
Bergantung pada jenis parallelepiped, formula ini dapat dipermudahkan.

Oleh itu, kita mempunyai, sebagai contoh, bahawa jumlah orthoedro akan diberikan oleh

V = ABC.

Di mana a, b dan c mewakili panjang tepi orthoedro.

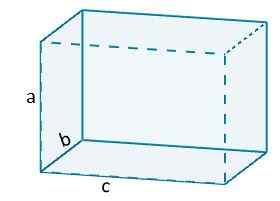
Dan dalam kes tertentu kiub adalah

V = a³

Contoh 1

Terdapat tiga model yang berbeza untuk kotak kuki dan anda mahu.

Yang pertama adalah kiub yang kelebihannya mempunyai panjang a = 10 cm.

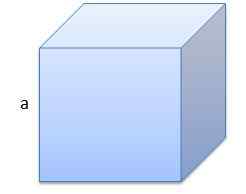
Kelantangannya ialah v = 1000 cm³

Yang kedua ialah b = 17 cm, c = 5 cm, d = 9 cm.

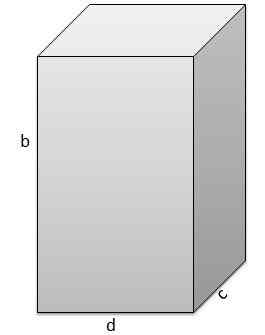
Dan oleh itu jumlahnya ialah v = 765 cm³

Dan yang ketiga mempunyai e = 9 cm, f = 9 cm dan g = 13 cm.

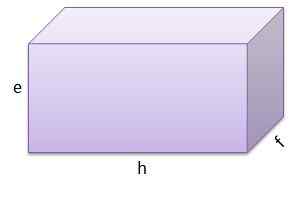
Dan jumlahnya ialah V = 1053 cm³

Boleh melayani anda: jenis sudut, ciri dan contoh

Oleh itu, kotak dengan jumlah terbesar adalah yang ketiga.

Kaedah lain untuk mendapatkan kelantangan paralelepiped adalah untuk menggunakan algebra vektor. Khususnya, produk skalar triple.

Salah satu tafsiran geometri produk skalar triple ialah jumlah parallelepiped, yang tepinya adalah tiga vektor yang berkongsi puncak yang sama sebagai titik permulaan.

Dengan cara ini, jika kita mempunyai parallelepiped dan kita ingin tahu berapa jumlahnya, sudah cukup untuk mewakilinya dalam sistem koordinat dalam r r dalam r³ bertepatan dengan salah satu simpang dengan asal.

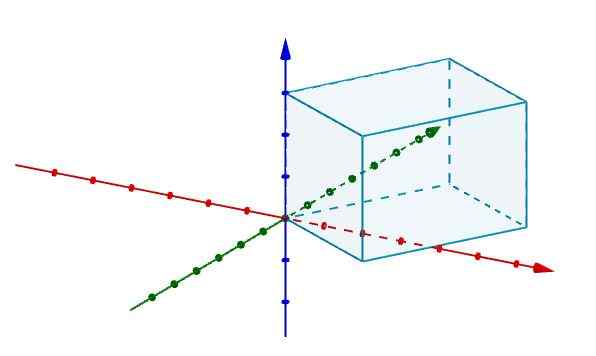
Kemudian kami mewakili tepi yang setuju pada asalnya dengan vektor, seperti yang ditunjukkan dalam angka itu.

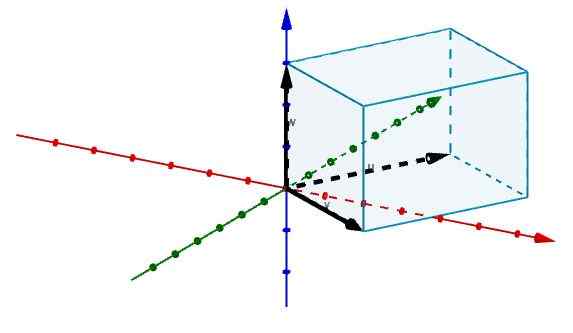
Dan dengan cara ini kita mempunyai jumlah parallelepiped yang diberikan oleh

V = | AXB ∙ C |

Atau bersamaan, kelantangan adalah penentu matriks 3 × 3, dibentuk oleh komponen vektor tepi.

Contoh 2

Dengan mewakili parallelepiped berikut dalam r³ Kita dapat melihat bahawa vektor yang menentukannya adalah yang berikut

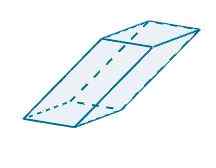
u = (-1, -3.0), v = (5, 0, 0) dan w = (-0.25, -4, 4)

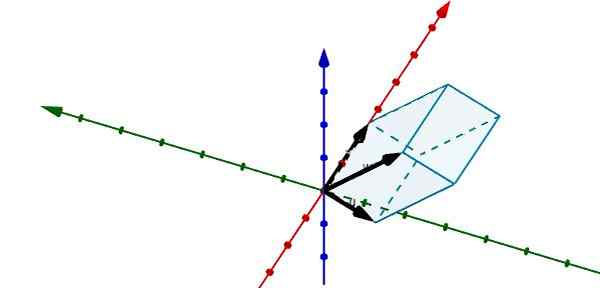
Menggunakan produk skalar triple yang kami ada

V = | (Uxv) ∙ w |

Uxv = (-1, -3.0) x (5, 0, 0) = (0.0, -15)

(Uxv) ∙ w = (0.0,- 15) ∙ (-0.25, -4, 4) = 0 + 0 + 4 ( - 15) = - 60

Ini menyimpulkan bahawa v = 60

Pertimbangkan sekarang selari berikut dalam r³ yang tepi ditentukan oleh vektor

A = (2, 5, 0), b = (6, 1, 0) dan C = (3, 4, 4)

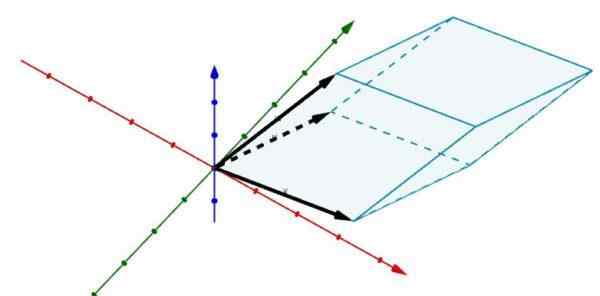
Menggunakan penentu memberi kita itu

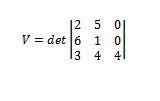
Oleh itu kita mempunyai jumlah yang dikatakan parallelepiped adalah 112.

Kedua -duanya adalah cara yang setara untuk mengira kelantangan.

Perfect parallelepiped

Ia dikenali sebagai batu bata Euler (atau blok euler) ke orthoedro yang memenuhi harta yang panjangnya tepi dan panjang pepenjuru setiap wajahnya adalah nombor keseluruhan.

Walaupun Euler bukan saintis pertama yang mempelajari orthoeders yang memenuhi harta itu, dia mendapat hasil yang menarik mengenai mereka.

Bata Euler terkecil ditemui oleh Paul Halcke (1662-1731) dan panjang tepinya adalah A = 44, b = 117 dan C = 240.

Masalah terbuka dalam teori nombor adalah seperti berikut:

Adakah terdapat orthoeders yang sempurna?

Pada masa ini, soalan ini masih tidak ada jawapan, kerana tidak mungkin untuk membuktikan bahawa tidak ada badan, tetapi tidak ada yang dijumpai.

Apa yang telah ditunjukkan setakat ini adalah bahawa parallelepiped yang sempurna lakukan. Yang pertama ditemui mempunyai panjang tepi nilai 103, 106 dan 271.

Rujukan

1. Lelaki, r. (1981). Masalah yang tidak diselesaikan dalam teori bilangan. Springer.
2. Landaverde, f. d. (1997). Geometri. Kemajuan.
3. Leithold, l. (1992). Pengiraan dengan geometri analitik. Harla, s.Ke.
4. Rendon, a. (2004). Lukisan Teknikal: Notebook Aktiviti 3 Baccalaureate ke -2. Tebar.
5. Resnick, r., Halliday, d., & Krane, k. (2001). Fizik Vol. 1. Mexico: Continental.