Menunggu formula dan persamaan baris, perwakilan, contoh

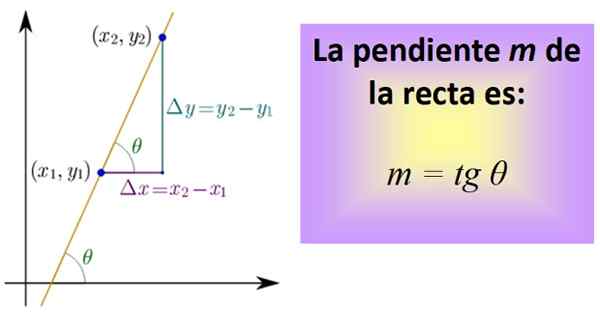
The Garis yang belum selesai Ia adalah tangen sudut θ yang bentuk garis ini dengan paksi mendatar, yang oleh konvensyen diukur ke arah yang bertentangan dengan tangan jam. Lereng garis mana -mana sentiasa malar dan itulah sebabnya ia adalah salah satu ciri yang paling penting.

Untuk mengira, anda perlu mengetahui dua titik garis, yang koordinatnya (x x₁,dan₁) dan (x₂,dan₂). Antara kedua -dua titik segmen ditarik yang dimiliki oleh garis dan kemudian segmen yang mewakili jarak antara x ditarik₁ dan x₂, dan antara dan₁ dan dan₂, Seperti pada angka yang lebih rendah.

Rajah 1. Cerun garis adalah tangen sudut θ. Sumber: Wikimedia Commons.

Tiga segmen membentuk segitiga kanan yang kakinya: Δx = x₂ - x₁  dan Δy = dan₂ - dan₁. Masing -masing sesuai dengan anjakan mendatar dan menegak lain.

Sekarang kota ditakrifkan, dipanggil tangen sudut θ dan disingkat Tg θ, yang tepatnya cerun m garis:

m = tg θ = Δy / Δx

Perhatikan bahawa untuk garis, sudut ini tetap malar, tanpa mengira titik yang diambil untuk mengira tangennya. Walau apa pun, nilai ini memberi kita ukuran bagaimana cenderungnya adalah garis.

Melalui koordinat titik yang dipilih, formula cerun kekal:

M = (y - y₁ ) / (X₂ - x₁)

[TOC]

Perwakilan grafik

Di bawah ini kita mempunyai beberapa situasi di mana konsep cerun adalah relevan. Nilainya dengan mudah boleh dikira dengan mengukur anjakan menegak dan mendatar masing -masing, dan kemudian membuat kota yang ditunjukkan pada mulanya.

Ini memberi kita idea tentang cerun atau penurunan beberapa struktur, seperti jalan, bumbung atau jalan:

Boleh melayani anda: pensampelan rawak: metodologi, kelebihan, kekurangan, contoh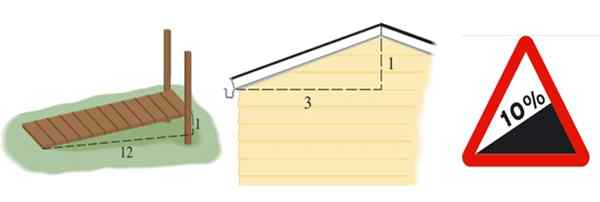 Rajah 2. Dari kiri ke kanan cerun jalan, bumbung dan cerun jalan, yang terakhir dinyatakan dalam peratusan. Sumber: Stewart, J. Precáculculo dan Wikimedia Commons (Imej Betul).

Lereng jalan yang ditunjukkan dalam Rajah 2 di sebelah kiri adalah m = 1/12, bumbung adalah m = 1/3 dan jalan dinyatakan dalam peratusan. Peratusan 10 % bermakna bahawa untuk setiap 100 meter yang maju secara mendatar, mereka mendapat 10 meter tinggi:

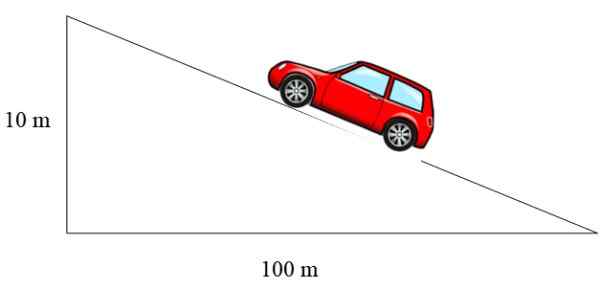Rajah 3. Kenderaan naik melalui cerun yang cerunnya 10%. Sumber: f. Zapata.

Dalam kes ini cerun adalah 10/100 = 0.1, yang dinyatakan sebagai peratusan sama dengan 10%.

Jenis cerun

Cerun garis boleh positif, negatif atau batal. Contohnya garis yang ditunjukkan dalam Rajah 1 mempunyai cerun positif. Kami menghargainya dengan segera kerana kita melihat bahawa garis itu "diangkat" jika kita melihatnya dari kiri ke kanan.

Sekiranya garis turun melihatnya dari kiri ke kanan, maka cerunnya negatif. Dan apabila garis mendatar, cerunnya adalah batal.

Akhirnya, untuk garis menegak, cerun tidak ditakrifkan.

Perwakilan grafik setiap jenis terdapat di bawah:

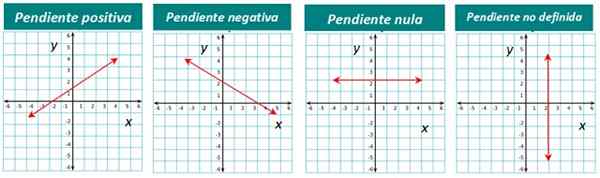Rajah 4. Garis mengikut cerun anda. Sumber: f. Zapata.

Bagaimana cerun dikira garis?

Mengira cerun sangat mudah, anda hanya perlu mencari anjakan menegak dan anjakan mendatar, dan kemudian membuat kota antara kedua -dua.

Apabila anda mempunyai lukisan garis dalam pesawat Cartesian, anjakan ini memilih mana -mana dua titik garis p₁ Dan p₂, Menentukan koordinat mereka dan menggunakan definisi yang diberikan pada mulanya:

Boleh melayani anda: Apa yang mewakili panjang anjakan segi enam

M = (y - y₁ ) / (X₂ - x₁ )

Oleh kerana nilai cerun bebas daripada pilihan p₁ Dan p₂ , Kami akan memilih titik P koordinat (x, y) yang dimiliki oleh garis, yang koordinatnya tidak diketahui, dan titik lain p₁ Koordinatnya ialah: (x₁,dan₁).

Cerun adalah:

M = (y - y₁) / (x - x₁)

Kita dapat membersihkan dan:

dan - dan₁ = m (x - x₁)

Sekarang anggap titik p₁ Ia adalah persimpangan garis dengan paksi menegak, koordinat (0, b). Menggantikan ini dalam persamaan sebelumnya:

dan - b = m (x - 0) → y = mx + b

Ungkapan ini dikenali sebagai persamaan garis dalam bentuk Menunggu - persimpangan, kerana garis itu ditentukan secara tegas apabila cerun dan persimpangannya dengan paksi menegak diketahui.

Mengetahui hanya cerun tidak cukup untuk mencirikan garis di atas kapal terbang, kerana Infinite Straight boleh mempunyai cerun yang sama, yang bermaksud bahawa mereka selari, tetapi melalui mata lain.

Latihan yang diselesaikan

- Latihan 1

Cari cerun garisan yang ditunjukkan dalam angka berikut:

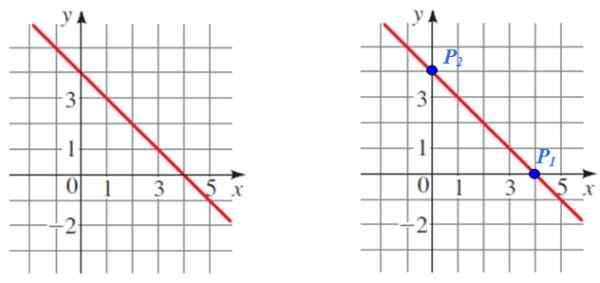Rajah 5. Melalui graf garis dua mata dipilih untuk mengira cerunnya. Sumber: f. Zapata.

Penyelesaian

P₁ Dan p₂ Mereka adalah dua mata yang mudah untuk dibaca untuk pengiraan, juga menyatakan bahawa mereka adalah persimpangan masing -masing dengan paksi koordinat.

Koordinat setiap titik adalah:

P₁ (4.0) dan P₂ (0.4)

Dengan menggantikan persamaan cerun:

m = (4 - 0) / (0 - 4) = 4 / ( - 4) = -1

Cerun negatif, yang dijangka setelah memerhatikan grafik.

Boleh melayani anda: Nombor kompleks: sifat, contoh, operasi

- Latihan 2

Cari persamaan garis yang melewati titik (1, -6) dan selari dengan garis y = 2x - 3.

Penyelesaian

Cerun garis yang dicari harus sama dengan y = 2x - 3, kerana selari. Untuk garis ini cerun adalah m = 2, oleh itu yang kita cari mempunyai bentuk:

dan - dan₁ = 2 (x - x₁)

Sekarang kita menggantikan titik di mana garis kita berlalu: x₁ = 1 dan₁ = -6.

dan - (-6) = 2 (x - 1)

Oleh itu y = 2x - 2 - 6 → y = 2x - 8

Contoh

Dua kuantiti boleh dikaitkan sedemikian rupa sehingga graf anda adalah garis lurus. Dalam hal ini dikatakan bahawa jumlahnya mempunyai ketergantungan linear dan cerun garis dapat ditafsirkan sebagai alasan untuk perubahan satu pemboleh ubah kepada yang lain.

Contoh 1

Katakan kolam dipenuhi dengan air ke a kadar tetap dalam masa. Sememangnya, lebih banyak masa berlalu, lebih banyak air disimpan. Nah, kadar yang dipenuhi kolam adalah tepatnya cerun garis yang berkaitan dengan jumlah ke semasa:

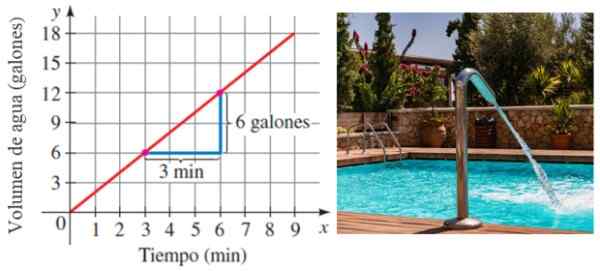Rajah 6. Cerun sebagai alasan perubahan. Sumber: Stewart, J./Pxfuel.

Dalam contoh ini, kolam diisi pada kadar 6/3 gelen seminit atau 2 gelen/minit.

Contoh 2

Apabila mudah alih bergerak dalam garis lurus dengan kelajuan malar, cerun graf kedudukan bergantung pada masa adalah tidak lain daripada kelajuan tersebut. Grafik menunjukkan mudah alih dengan kelajuan positif, yang bermaksud bahawa ia bergerak jauh dari asal.

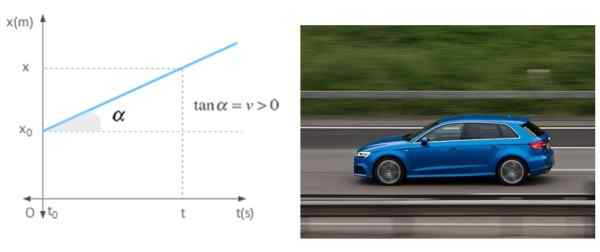Rajah 7. Cerun graf versus masa adalah kelajuan mudah alih dalam pergerakan rectilinear seragam. Sumber: Wikimedia Commons/Pixabay.

Rujukan

1. Alvarez, J. Cerun jalan. Pulih dari: geogra.adalah.
2. Carena, m. 2019. Manual Matematik PraUniversiti. Universiti Kebangsaan Pantai.
3. Hoffman, J. Pemilihan masalah matematik. Jilid 4.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Stewart, J. 2006. Preccculment: Matematik untuk Pengiraan. 5th. Edisi. Pembelajaran Cengage.
6. Zill, d. 1984. Algebra dan trigonometri. McGraw Hill.