Definisi poligon cembung, elemen, sifat, contoh

A Convex Polygon Ia adalah angka geometri yang terkandung dalam satah yang dicirikan kerana ia mempunyai semua pepenjuru di dalam dan sudutnya kurang dari 180º. Antara sifatnya adalah seperti berikut:

1) Ia terdiri daripada segmen n berturut -turut di mana segmen terakhir menyertai yang pertama. 2) Tiada segmen yang diseberang sedemikian. 3) Setiap sudut dari rantau dalaman adalah lebih rendah daripada sudut rata.

Rajah 1. Poligon 1, 2 dan 6 adalah cembung. (Disediakan oleh Ricardo Pérez).

Cara mudah untuk menentukan sama ada poligon adalah cembung atau tidak mempertimbangkan garis yang melewati salah satu sisinya, yang menentukan dua semiplanes. Jika pada setiap baris yang berlalu di satu pihak, sisi lain dari poligon berada dalam semiplane yang sama, maka ia adalah poligon cembung.

[TOC]

Unsur poligon

Setiap poligon terdiri daripada unsur -unsur berikut:

- Sisi

- Simpang

Sisi masing -masing segmen berturut -turut yang membentuk poligon. Dalam poligon tidak ada segmen yang membuatnya boleh mempunyai akhir terbuka, dalam hal ini akan ada garis poligon tetapi bukan poligon.

Vertices adalah titik kesatuan dua segmen berturut -turut. Dalam poligon, bilangan simpang selalu sama dengan bilangan sisi.

Sekiranya dua sisi atau segmen salib poligon, maka anda mempunyai poligon salib. Titik persimpangan tidak dianggap sebagai puncak. Poligon salib adalah poligon bukan konvensial. Poligon yang terhempas adalah poligon melintasi dan oleh itu tidak cembung.

Ia dapat melayani anda: geometri analisis

Apabila poligon mempunyai semua sisi panjang yang sama, maka ada poligon biasa. Semua poligon biasa adalah cembung. 

Poligon cembung dan bukan cembung

Rajah 1 menunjukkan beberapa poligon, beberapa di antaranya adalah cembung dan yang lain tidak. Mari kita menganalisis mereka:

Nombor 1 adalah poligon tiga -sisi (segitiga) dan semua sudut dalaman kurang dari 180º, oleh itu ia adalah poligon cembung. Semua segitiga adalah poligon cembung.

Nombor 2 adalah poligon empat yang berdepan (segi empat tepat) di mana tidak ada sisi yang dipintas dan juga setiap sudut dalaman kurang dari 180º. Ia kemudiannya adalah poligon cembung empat orang (cembung kuadrilateral).

Sebaliknya, nombor 3 adalah poligon empat yang berpandu tetapi salah satu sudut dalamannya lebih besar daripada 180º, jadi ia tidak memenuhi syarat convexity. Ia.

Nombor 4 adalah poligon empat -penyepit (sisi), dua daripadanya dipintas. Empat sudut dalamannya kurang dari 180º, tetapi sebagai dua sisi menyeberang mereka adalah poligon silang bukan conveks (silang kuadrilateral).

Kes lain ialah nombor 5. Ini adalah poligon lima yang berpandu, tetapi sebagai salah satu sudut dalamannya lebih besar daripada 180º, maka ada poligon cekung.

Akhirnya, nombor 6, yang juga mempunyai lima sisi, mempunyai semua sudut pedalamannya kurang dari 180º, jadi ia adalah poligon cembung lima orang (cembung pentagon).

Boleh melayani anda: ralat pensampelan: formula dan persamaan, pengiraan, contoh

Convex Polygon Properties

1- Poligon yang tidak rusak atau poligon sederhana membahagikan satah yang mengandunginya ke dalam dua wilayah. Rantau dalaman dan kawasan luar, sebagai poligon sempadan antara kedua -dua wilayah.

Tetapi jika tambahan poligon adalah cembung, maka terdapat rantau dalaman yang hanya berkaitan, yang bermaksud bahawa mengambil dua titik di rantau dalaman, ia selalu dapat disatukan oleh segmen yang dimiliki secara keseluruhannya ke rantau dalaman.

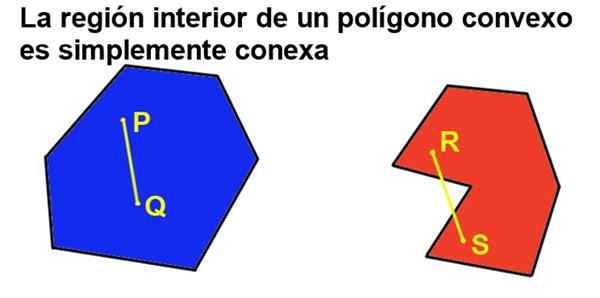Rajah 2. Poligon cembung hanya berkaitan, sementara cekung tidak. (Disediakan oleh Ricardo Pérez).

2- Sudut dalaman poligon cembung kurang dari sudut rata (180º).

3- Semua titik dalaman poligon cembung selalu tergolong dalam salah satu yang ditakrifkan oleh garis yang melewati dua simpul berturut-turut.

4- Dalam poligon cembung semua pepenjuru sepenuhnya terkandung di rantau poligon dalaman.

5- Titik dalaman poligon cembung milik keseluruhannya dengan sektor sudut cembung yang ditakrifkan oleh setiap sudut dalaman.

6- Setiap poligon di mana semua simpangnya berada di lilitan adalah poligon cembung yang dipanggil poligon siklik.

7- Setiap poligon kitaran adalah cembung, tetapi tidak setiap poligon cembung adalah kitaran.

8- Setiap poligon yang tidak hancur (poligon sederhana) yang mempunyai semua sisi panjang yang sama adalah cembung dan dikenali sebagai poligon biasa.

Pepenjuru dan sudut dalam poligon cembung

9- Jumlah bilangan pepenjuru poligon cembung N sisi diberikan oleh formula berikut:

Ia dapat melayani anda: grafik polybal

N = ½ n (n - 3)

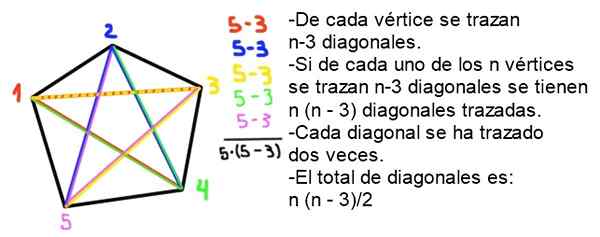
Demonstrasi: Dalam poligon cembung N sisi setiap puncak, n - 3 pepenjuru ditarik, kerana puncak itu sendiri dan kedua -dua yang bersebelahan dikecualikan. Oleh kerana terdapat simpul n, mereka ditarik dalam jumlah n - 2) pepenjuru, tetapi setiap pepenjuru ditarik dua kali, jadi bilangan pepenjuru (tanpa pengulangan) adalah n (n -2)/2.

10- Jumlah sudut dalaman poligon cembung N sisi diberikan oleh hubungan berikut:

S = (n - 2) 180º

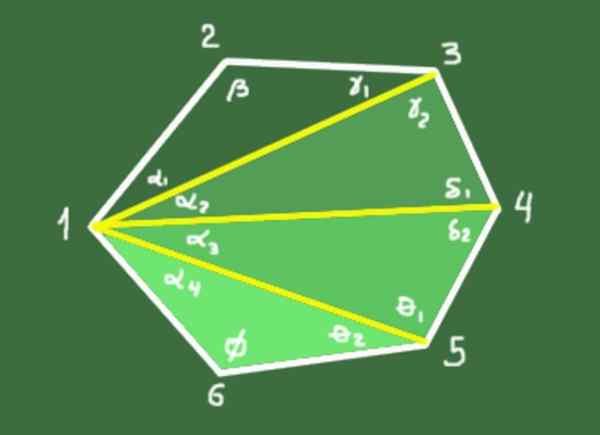
Demonstrasi: Diagonal N-3 diambil dari puncak yang menentukan segi tiga N-2. Jumlah sudut dalaman setiap segitiga adalah 180º. Jumlah jumlah sudut segitiga N-2 adalah (n-2)*180º, yang bertepatan dengan jumlah sudut dalaman poligon.

Contoh

Contoh 1

Hexagon kitaran, ia adalah poligon enam dan enam simpang, tetapi semua simpang berada di lilitan yang sama. Semua poligon kitaran adalah cembung.

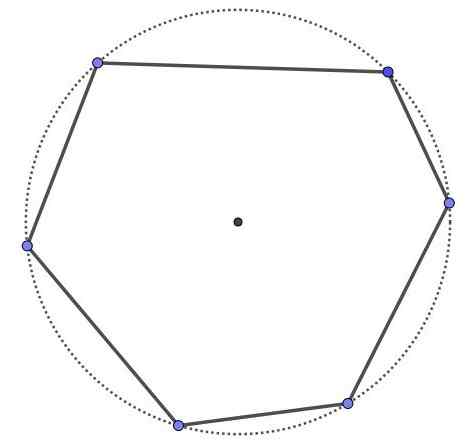Hexagon kitaran.

Contoh 2

Tentukan nilai sudut dalaman enegon biasa.

Penyelesaian: Enegon adalah poligon 9 yang disediakan, tetapi ia juga mengawal selia semua sisi dan sudutnya adalah sama.

Jumlah semua sudut dalaman poligon 9 -sided adalah:

S = (9 - 2) 180º = 7 * 180º = 1260º 

Tetapi terdapat 9 sudut dalaman ukuran yang sama α, jadi kesamaan berikut mesti dipenuhi:

S = 9 α = 1260º

Dari mana ia mengikuti bahawa ukuran α setiap sudut dalaman enegon biasa adalah:

α = 1260º/9 = 140º