Penjelasan tekanan manometrik, formula, persamaan, contoh

The Tekanan tolok P_m Ia adalah satu yang diukur berhubung dengan tekanan rujukan, yang dalam kebanyakan kes dipilih sebagai tekanan atmosfera p_Atm di paras laut. Ia adalah a Tekanan relatif, istilah lain yang juga dikenali.

Cara lain di mana tekanan biasanya diukur membandingkannya dengan kekosongan mutlak, yang tekanannya selalu. Dalam kes ini terdapat perbincangan mengenai tekanan mutlak, yang mana kita akan menunjukkan bagaimana p_ke.

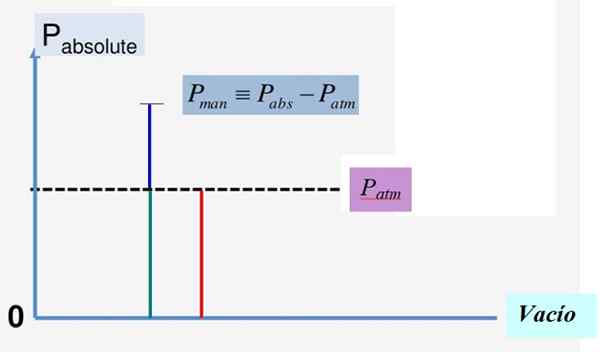
Rajah 1. Tekanan mutlak dan tekanan manometrik. Sumber: f. Zapata.

Hubungan matematik antara ketiga -tiga kuantiti ini adalah:

P_ke = P_Atm + P_m

Oleh itu:

P_m = P_ke - P_Atm

Rajah 1 dengan mudah menggambarkan hubungan ini. Oleh kerana tekanan vakum adalah 0, tekanan mutlak sentiasa positif dan yang sama berlaku untuk tekanan atmosfera p_Atm.

Tekanan manometrik biasanya digunakan untuk menunjukkan tekanan di atas tekanan atmosfera, seperti yang dibawa oleh tayar atau yang di bahagian bawah laut atau kolam, yang dikenakan oleh berat lajur air. Dalam kes ini p_m > 0, sejak p_ke > P_Atm.

Walau bagaimanapun, terdapat tekanan mutlak di bawah p_Atm. Dalam kes ini p_m < 0 y recibe el nombre de tekanan vakum Dan ia tidak boleh dikelirukan dengan tekanan vakum yang telah diterangkan, yang merupakan ketiadaan zarah yang mampu memberi tekanan.

[TOC]

Formula dan persamaan

Tekanan dalam cecair -liquid atau gas -adalah salah satu pembolehubah yang paling penting dalam kajiannya. Dalam cecair pegun, tekanan adalah sama pada semua titik ke kedalaman yang sama tanpa mengira orientasi, sementara pergerakan cecair dalam paip disebabkan oleh perubahan tekanan.

Tekanan purata ditakrifkan sebagai kuota antara daya tegak lurus ke permukaan F_⊥ dan kawasan permukaan A, yang dinyatakan secara matematik seperti berikut:

P = f_⊥ /Ke

Tekanan adalah kuantiti skalar, dimensinya berkuat kuasa per unit kawasan. Unit ukuran anda dalam Sistem Unit Antarabangsa (SI) adalah Newton/m², Dipanggil Pascal dan disingkat sebagai PA, sebagai penghormatan kepada Blaise Pascal (1623-1662).

Gandaan seperti Kilo (10³) dan mega (10⁶) Mereka sering digunakan, kerana tekanan atmosfera biasanya dalam lingkungan 90.000 - 102.000 PA, yang sama dengan: 90 - 102 kPa. Tekanan urutan mega pascals tidak jarang, jadi penting untuk membiasakan diri dengan awalan.

Di Anglo -Saxon unit tekanan diukur dalam pound/kaki², Walau bagaimanapun, perkara biasa perlu dilakukan dalam pound/inci² Sama ada psi (Pound-force per inci persegi).

Boleh melayani anda: pemindahan haba: undang -undang, borang penghantaran, contoh

Variasi tekanan dengan kedalaman

Semakin kita membenamkan diri di dalam air kolam atau di laut, semakin banyak tekanan yang kita alami. Sebaliknya, peningkatan ketinggian, tekanan atmosfera berkurangan.

Purata tekanan atmosfera di paras laut ditubuhkan pada 101300 PA atau 101.3 kPa, manakala di lubang Mariana di Pasifik Barat - kedalaman terbesar yang diketahui - kira -kira 1000 kali lebih tinggi dan di bahagian atas Everest hanya 34 kPa.

Jelas bahawa tekanan dan kedalaman (atau ketinggian) berkaitan. Untuk mengetahui dalam kes cecair berehat (keseimbangan statik) ia dianggap sebagai bahagian bendalir dengan cecair berbentuk cakera, terkurung dalam bekas, (lihat Rajah 2). Cakera mempunyai bahagian silang Ke, berat DW dan ketinggian Dy.

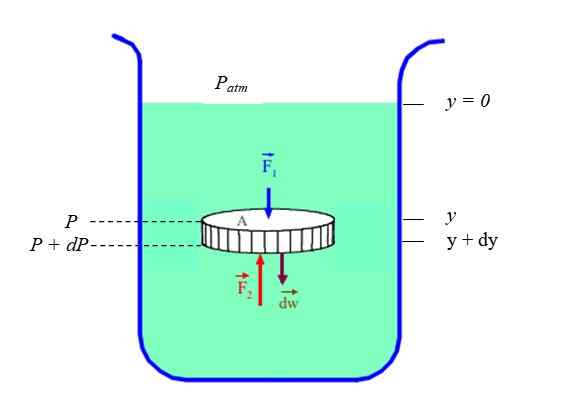Rajah 2. Unsur pembezaan cecair keseimbangan statik. Sumber: Fanny Zapata.

Kami akan menelefon P pada tekanan yang wujud secara mendalam "dan"Dan P + DP pada tekanan yang wujud secara mendalam (dan + dy). Oleh kerana ketumpatan ρ cecair adalah alasan antara jisimnya DM dan jumlahnya Dv, Kamu perlu:

ρ = dm/ dv ⇒ dm = ρ.Dv

Oleh itu beratnya DW elemen adalah:

dw = g. Dm = ρ.g.Dv

Dan sekarang undang -undang kedua Newton terpakai:

Σ f_dan = F₂ - F₁ - DW = 0

(P + dp).A - p.Ke - ρ.g.Dv = 0

(P + dp).A - p.Ke - ρ.g. Ke. Dy = 0

Dp = ρ.g.Dy

Penyelesaian persamaan pembezaan 

Mengintegrasikan kedua -dua belah pihak dan mempertimbangkan kepadatan itu ρ, serta graviti g Mereka tetap, ada ungkapan yang dicari:

P₂ - P₁ = ΔP = ρ.g.(dan₂ - dan₁)

Δp = ρ.g. Δdan

Sekiranya dalam ungkapan sebelumnya ia dipilih P₁ seperti tekanan atmosfera dan dan₁ Seperti permukaan cecair, maka dan₂ Ia terletak pada kedalaman h dan ΔP = p₂ - P_Atm Ia adalah tekanan manometrik bergantung pada kedalaman:

P_m = ρ.g.h

Sekiranya anda memerlukan nilai tekanan mutlak, tekanan atmosfera hanya ditambah kepada hasil sebelumnya.

Contoh

Untuk mengukur tekanan manometrik peranti digunakan tekanan tolok, yang umumnya menawarkan perbezaan tekanan. Akhirnya, prinsip pengoperasian manometer tekanan U -yang akan diterangkan, tetapi sekarang mari kita lihat beberapa contoh penting dan akibat dari persamaan yang ditolak sebelumnya.

Prinsip Pascal

Persamaan ΔP = ρ.g.(dan₂ - dan₁) Ia boleh ditulis sebagai  P = po + ρ.g.h, di mana P adalah tekanan pada kedalaman h, manakala P_{Sama ada} Ia adalah tekanan pada permukaan bendalir, biasanya P_Atm.

Jelas setiap kali anda meningkat PO, kenaikan P dalam jumlah yang sama, selagi ia adalah cecair yang ketumpatannya tetap. Ini adalah apa yang sepatutnya dipertimbangkan ρ tetap dan letakkan di luar integral yang diselesaikan di bahagian sebelumnya.

Boleh melayani anda: pergerakan harmonik sederhana

Prinsip Pascal menyatakan bahawa sebarang kenaikan tekanan cecair yang terkurung dalam keseimbangan, dihantar tanpa sebarang variasi kepada semua titik cecair tersebut. Melalui harta ini, ada kemungkinan untuk membiak F₁ digunakan di sebelah kiri kecil di sebelah kiri, dan dapatkan F₂ di sebelah kanan.

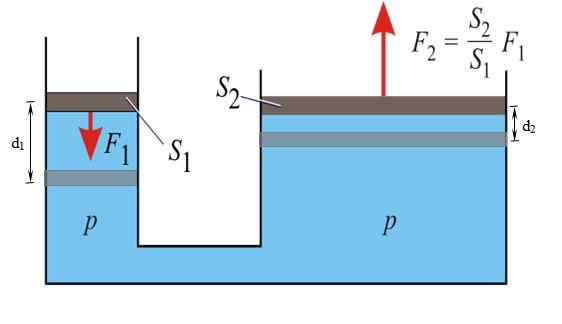Rajah 3. Dalam akhbar hidraulik, prinsip Pascal digunakan. Sumber: Wikimedia Commons.

Brek kereta berfungsi di bawah prinsip ini: daya yang agak kecil digunakan pada pedal, yang menjadi daya utama pada silinder brek pada setiap roda, terima kasih kepada cecair yang digunakan dalam sistem.

Paradoks hidrostatik Stevin

Paradoks hidrostatik menyatakan bahawa daya yang disebabkan oleh tekanan cecair di bahagian bawah bekas boleh sama, lebih besar atau lebih rendah daripada berat bendalir itu sendiri. Tetapi apabila meletakkan bekas di atas skala, ia biasanya akan merekodkan berat bendalir (ditambah dengan salah satu bekas tentu saja). Cara Menjelaskan Paradoks Ini?

Kami bermula dari fakta bahawa tekanan di bahagian bawah bekas bergantung secara eksklusif pada kedalaman dan bebas dari bentuk, seperti yang disimpulkan di bahagian sebelumnya.

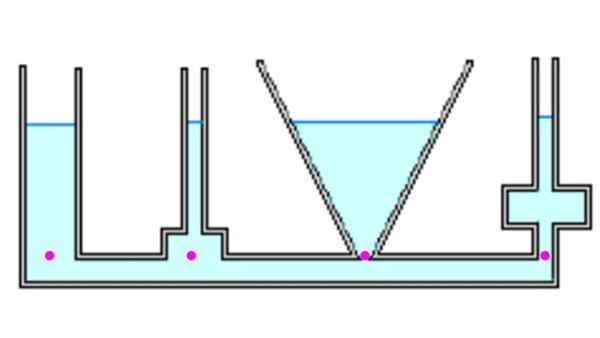Rajah 4. Cecair mencapai ketinggian yang sama di semua bekas dan tekanan di latar belakang adalah sama. Sumber: f. Zapata.

Mari lihat beberapa bekas yang berbeza. Apabila disampaikan, apabila mereka dipenuhi dengan cecair, semua orang mencapai ketinggian yang sama h. Titik yang menonjol berada pada tekanan yang sama, kerana mereka berada di kedalaman yang sama. Walau bagaimanapun, daya yang disebabkan oleh tekanan pada setiap titik boleh berbeza dari berat badan, (lihat Contoh 1 di bawah).

Latihan

Latihan 1

Bandingkan daya yang dikenakan oleh tekanan di bahagian bawah setiap bekas dengan berat bendalir, dan terangkan mengapa perbezaan, jika ada.

Bekas 1 

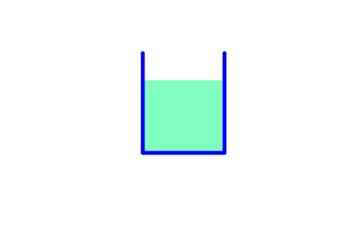Rajah 5. Tekanan di latar belakang adalah sama dengan magnitud dengan berat bendalir. Sumber: Fanny Zapata.

Di dalam bekas ini, kawasan asas adalah, oleh itu:

Berat cecair: mg = ρ.V.G = ρ . Ke .h . g

Tekanan di bahagian bawah: ρ. g. h

Daya akibat tekanan: f = p.A = ρ. g. h. Ke

Berat dan daya akibat tekanan adalah sama.

Bekas 2 

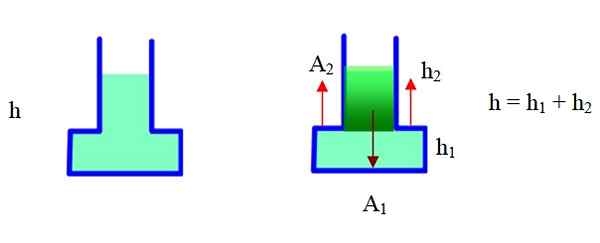Rajah 6. Daya yang disebabkan oleh tekanan dalam bekas ini lebih besar daripada berat badan. Sumber: f. Zapata.

Bekas mempunyai bahagian sempit dan sebahagian besar. Dalam skim yang betul ia telah dibahagikan kepada dua bahagian dan akan menggunakan geometri untuk mencari jumlah keseluruhan. Kawasan a₂ adalah luaran ke bekas, h₂ Ia adalah ketinggian bahagian sempit, h₁ Ia adalah ketinggian bahagian yang luas (asas).

Boleh melayani anda: Pleiades: Sejarah, Asal dan Komposisi

Kelantangan lengkap ialah kelantangan asas + kelantangan bahagian sempit. Dengan data ini anda ada:

Berat Cecair: m . G = ρ . g. V = ρ . g. [Ke₁ .h₁+ (Kepada₁ -Ke₂) .h₂] =

= ρ . g (a₁.ha₂h₂) = ρ . g . Ke₁.H - ρ . g . Ke._. h₂ (Penggunaan h = h₁ +h₂)

Tekanan di bahagian bawah: p = ρ. g. h

Daya di bahagian bawah kerana tekanan: f = p. Ke₁ = ρ. g. h. Ke₁

Membandingkan berat bendalir dengan daya disebabkan oleh tekanan yang diperhatikan bahawa ini lebih besar daripada berat badan.

Apa yang berlaku ialah bendalir juga menimbulkan kekuatan pada bahagian langkah dalam bekas (lihat anak panah merah angka) yang dimasukkan dalam pengiraan sebelumnya. Kekuatan melawan ini kepada mereka yang dikenakan dan berat yang direkodkan oleh skala adalah hasilnya. Menurut ini, magnitud berat adalah:

W = daya pada latar belakang - kekuatan pada bahagian yang berperingkat = ρ . g . Ke₁.H - ρ . g . Ke._. h₂

Latihan 2

Angka ini menunjukkan tolok tekanan tiub terbuka. Ia terdiri daripada tiub U, di mana salah satu hujungnya berada pada tekanan atmosfera dan yang lain menghubungkan ke S, sistem yang tekanannya akan diukur.

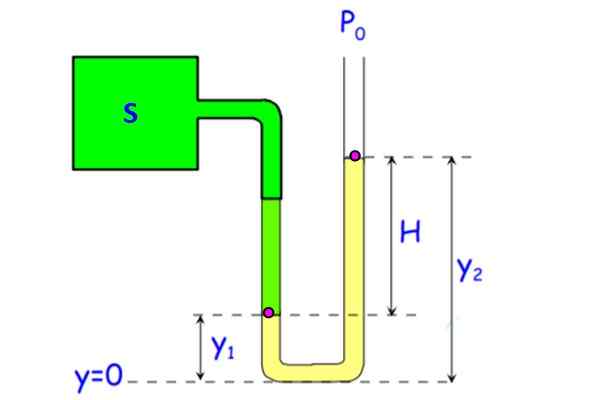Rajah 7. Tolok tekanan tiub terbuka. Sumber: f. Zapata.

Cecair di dalam tiub (dalam kuning dalam angka) boleh menjadi air, walaupun merkuri digunakan untuk mengurangkan saiz peranti. (Perbezaan 1 atmosfera atau 101.3 kPa memerlukan lajur 10 air.3 meter, tiada mudah alih).

Diminta untuk mencari tekanan manometrik P_m Dalam sistem S, bergantung pada ketinggian h lajur cecair.

Penyelesaian

Tekanan di latar belakang untuk kedua -dua cabang tiub adalah sama, kerana berada dalam kedalaman yang sama. Biarkan p_Ke Tekanan di titik A, terletak di dan₁ Dan p_B orang -orang B yang berada di ketinggian dan₂. Oleh kerana titik B terletak di antara muka bendalir dan udara, tekanan ada p_{Sama ada}. Dalam cawangan tolok tekanan ini, tekanan di bahagian bawah adalah:

PO + ρ.g.dan₂

Bagi bahagiannya, tekanan di bahagian bawah untuk cawangan kiri adalah:

P + ρ.g.dan₁

Di mana p adalah tekanan mutlak sistem dan ρ adalah ketumpatan bendalir. Sama dengan kedua -dua tekanan:

PO + ρ.g.dan₂ = P +ρ.g.dan₁

Penjelasan P:

P = po + ρ.g.dan₂ - ρ.g.dan₁ = Po + ρ.g (dan₂ - dan₁) = Po + ρ.g. H

Oleh itu, tekanan manometrik P_m Ia diberikan oleh P - p_{Sama ada} = ρ.g. H Dan mempunyai nilainya, sudah cukup untuk mengukur ketinggian yang mana cecair manometrik meningkat dan membiaknya dengan nilai g dan ketumpatan bendalir.

Rujukan

1. Cimbala, c. 2006. Mekanik cecair, asas dan aplikasi. Mc. Graw Hill. 66-74.
2. Figueroa, d. 2005. Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 4. Cecair dan termodinamik. Diedit oleh Douglas Figueroa (USB). 3-25.
3. Mott, r. 2006. Mekanik cecair. Ke -4. Edisi. Pendidikan Pearson. 53-70.
4. Shaugnessy, e. 2005. Pengenalan kepada Mekanik Fluida.Oxford University Press. 51 - 60.
5. Stylianos, v. 2016. Untuk penjelasan ringkas mengenai paradoks hidrostatik klasik. Pulih dari: Haimgaifman.Fail.WordPress.com