Kebarangkalian teori bagaimana untuk mengeluarkannya, contoh, latihan

The Kebarangkalian teoritis (atau Laplace) bahawa peristiwa berlaku yang dimiliki oleh ruang sampel, di mana semua peristiwa mempunyai kebarangkalian kejadian yang sama, ia ditakrifkan dalam notasi matematik seperti: P (E) = N (E) / N ( S)

Di mana p (e) adalah kebarangkalian, diberikan sebagai nisbah antara jumlah hasil kemungkinan peristiwa e, yang kita panggil n (e), dibahagikan dengan jumlah jumlah n (s) kemungkinan hasil dalam ruang sampel s.

Rajah 1. Pada pelancaran dadu enam, kebarangkalian teoretikal bahawa wajah dengan tiga titik berada di bahagian atas adalah ⅙. Sumber: Pixabay.

Kebarangkalian teori adalah nombor sebenar antara 0 dan 1, tetapi ia sering dinyatakan dalam bentuk peratusan, di mana kebarangkalian akan menjadi nilai antara 0% dan 100%.

Mengira kebarangkalian kejadian peristiwa sangat penting dalam banyak bidang, seperti aktiviti pasaran saham, syarikat insurans, perjudian dan banyak lagi.

[TOC]

Bagaimana untuk mendapatkan kebarangkalian teori?

Kes ilustrasi adalah kes rifas atau loteri. Anggapkan bahawa 1.000 tiket untuk Rifar A Smartphone. Memandangkan undian dilakukan secara rawak, mana -mana tiket mempunyai peluang yang sama untuk menjadi pemenang. 

Untuk mencari kebarangkalian bahawa seseorang yang membeli tiket dengan nombor 81 menjadi pemenang, pengiraan berikut Kebarangkalian teoritis:

P (1) = 1/1.000 = 0.001 = 0.1%

Hasil sebelumnya ditafsirkan seperti berikut: Jika undian diulangi tak terhingga, setiap 1.000 kali tiket 81 akan dipilih, secara purata, sekali.

Sekiranya atas sebab apa pun seseorang memperoleh semua tiket pasti bahawa dia akan memenangi hadiah. Kebarangkalian memenangi hadiah jika anda mempunyai semua tiket yang dikira seperti berikut:

Ia dapat melayani anda: perimeter bulatan: Cara mengeluarkannya dan formula, latihan diselesaikan

P (1.000) = 1.000/1.000 = 1 = 100%.

Iaitu, kebarangkalian 1 atau 100% bermaksud bahawa ia benar -benar yakin bahawa hasil ini akan berlaku.

Sekiranya seseorang mempunyai 500 tiket kemungkinan menang atau kalah adalah sama. Kebarangkalian teori untuk memenangi hadiah dalam kes ini dikira seperti berikut:

P (500) = 500/1.000 = ½ = 0.5 = 50%.

Dia yang tidak membeli apa -apa tiket tidak mempunyai peluang untuk menang dan kebarangkalian teorinya ditentukan seperti ini:

 P (0) = 0/1.000 = 0 = 0%

Contoh

Contoh 1

Anda mempunyai mata wang dengan mahal di satu sisi dan Perisai atau meterai di pihak yang lain. Apabila mata wang dilancarkan, apakah kebarangkalian teoritis menjadi mahal?

P (mahal) = n (mahal) / N ( muka + perisai ) = ½ = 0.5 = 50%

Hasilnya ditafsirkan seperti berikut: Jika sejumlah besar siaran dibuat, secara purata dalam setiap 2 padang salah satu daripada mereka akan menghadapi.

Dalam segi peratusan, tafsiran hasilnya ialah membuat sejumlah besar pelancaran, secara purata setiap 100 daripadanya akan menghasilkan mahal.

Contoh 2

Di dalam kotak terdapat 3 guli biru, 2 guli merah dan 1 hijau. Apakah kebarangkalian teori bahawa apabila anda mendapat marmar dari kotak ini merah?

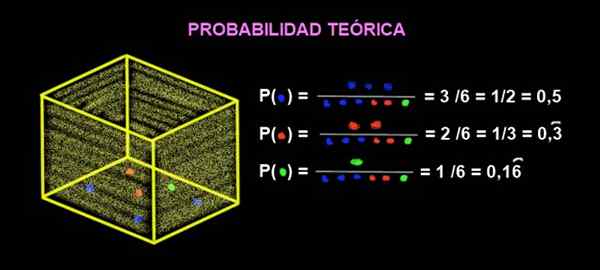Rajah 2. Kebarangkalian pengekstrakan kelereng warna. Sumber: f. Zapata.

Kebarangkalian yang berwarna merah adalah:

P (merah) = bilangan kes / bilangan kes yang menggalakkan

Iaitu:

P (merah) = bilangan guli merah / jumlah kelereng

Akhirnya, kebarangkalian bahawa marmar merah adalah:

P (merah) = 2/6 = ⅓ = 0.3333 = 33.33%

Walaupun kebarangkalian bahawa dengan mengekstrak marmar hijau adalah:

P (hijau) = ⅙ = 0.1666 = 16.66%

Akhirnya, kebarangkalian teoretikal mendapatkan dalam pengekstrakan buta marmar biru adalah: 

P (biru) = 3/6 = ½ = 0.5 = 50%

Ia dapat melayani anda: sifat radikal

Iaitu, setiap 2 percubaan hasilnya akan menjadi biru di salah satu daripada mereka dan warna lain dalam percubaan lain, di bawah premis bahawa marmar yang diekstrak itu diisi semula dan jumlah percubaannya sangat, sangat besar.

Latihan

Latihan 1

Tentukan kebarangkalian apabila melancarkan dadu nilai diperoleh kurang dari atau sama dengan 4.

Penyelesaian

Untuk mengira kebarangkalian bahawa peristiwa ini berlaku, definisi kebarangkalian teori akan dikenakan:

P (≤4) = bilangan kes / bilangan kes yang menggalakkan

P (≤5) = 5/6 = = 83.33%

Latihan 2

Cari kebarangkalian bahawa dalam dua padang berturut -turut dari dadu enam yang biasa, 2 kali 2 kali.

Penyelesaian

Untuk bertindak balas terhadap latihan ini, mudah untuk membuat gambar untuk menunjukkan semua kemungkinan. Angka pertama menunjukkan hasil dadu pertama dan yang kedua hasil yang lain.

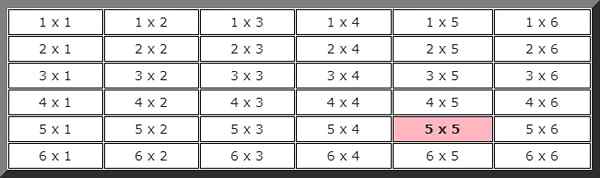
Untuk mengira kebarangkalian teoritis, kita perlu mengetahui jumlah kes yang mungkin, dalam kes ini seperti yang dapat dilihat dari jadual sebelumnya, terdapat 36 kemungkinan.

Juga memerhatikan lukisan yang berikut bahawa bilangan kes yang menguntungkan pada peristiwa yang dalam kedua -dua siaran berturut -turut datang 5 hanya 1, diserlahkan dengan warna, oleh itu kebarangkalian bahawa peristiwa ini akan berlaku adalah:

P (5 x 5) = 1/33.

Hasil ini juga dapat dicapai dengan menggunakan salah satu sifat kebarangkalian teoritis, yang menyatakan bahawa kebarangkalian gabungan dua peristiwa bebas adalah hasil dari kebarangkalian masing -masing.

Dalam hal ini kebarangkalian bahawa dalam pelepasan pertama 5 adalah ⅙. Pelancaran kedua adalah sepenuhnya bebas daripada yang pertama, oleh itu kebarangkalian bahawa 5 di kedua juga ⅙. Jadi kebarangkalian gabungan adalah:

Boleh melayani anda: derivatif separa: sifat, pengiraan, latihan

P (5 × 5) = P (5) P (5) = (1/6) (1/6) = 1/36.

Latihan 3

Cari kebarangkalian bahawa bilangan kurang daripada 2 keluar pada pelancaran pertama dan pada yang kedua nombor lebih besar daripada 2 keluar. 

Penyelesaian

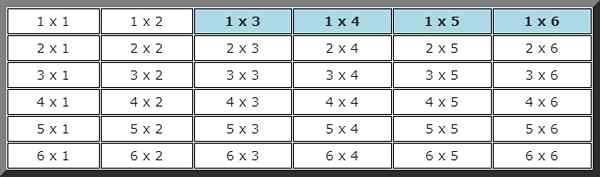
Sekali lagi anda perlu membina jadual acara yang mungkin, di mana pelancaran pertama kurang dari 2 dan pada kedua lebih tinggi daripada 2 digarisbawahi.

Secara keseluruhan terdapat 4 kemungkinan sebanyak 36. Dalam erti kata lain, kebarangkalian peristiwa ini adalah:

P (2) = 4/36 = 1/9 = 0.1111 = 11.11%

Menggunakan Teorem Kebarangkalian yang menyatakan:

Kebarangkalian berlakunya dua peristiwa bebas adalah sama dengan produk kebarangkalian individu.

Ia diperolehi hasil yang sama:

P (2) = (1/6) (4/6) = 4/36 = 0.1111 = 11.11%

Nilai yang diperoleh dengan prosedur ini bertepatan dengan hasil sebelumnya, melalui definisi teori atau klasik kebarangkalian.

Latihan 4

Berapakah kebarangkalian bahawa dengan melancarkan dua diberikan jumlah nilai adalah 7.

Penyelesaian

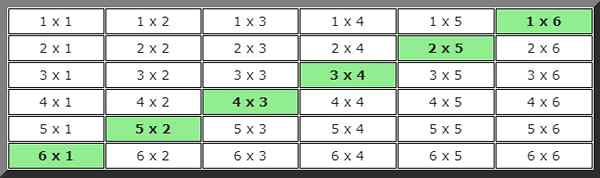
Untuk mencari penyelesaian dalam kes ini, gambar kemungkinan telah dibangunkan di mana kes -kes yang memenuhi syarat nilai -nilai adalah 7 telah ditunjukkan dalam warna.

Melihat meja, 6 kes yang mungkin dapat dikira, jadi kebarangkaliannya:

P (R & D II: 7) = 6/36 = 1/6 = 0.1666 = 16.66%

Rujukan

1. Canavos, g. 1988. Kebarangkalian dan Statistik: Aplikasi dan Kaedah. McGraw Hill.
2. DEVORE, J. 2012. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Ke -8. Edisi. Cengage.
3. Lipschutz, s. 1991. Siri Schaum: Kebarangkalian. McGraw Hill.
4. Obregón, i. 1989.Teori kebarangkalian. Editorial Limusa.
5. Walpole, r. 2007. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Pearson.