Produk silang

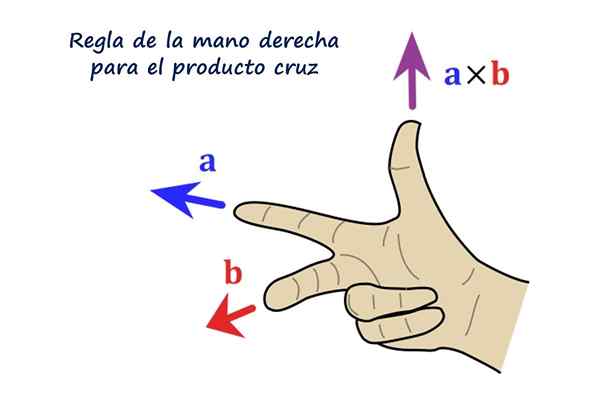
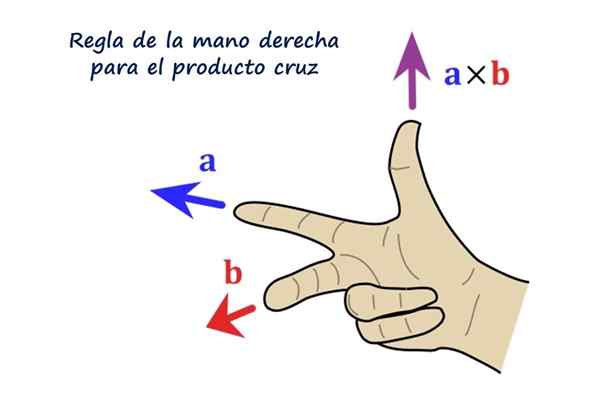Peraturan yang tepat untuk produk vektor. Sumber: f. Zapata.

Apakah produk silang atau produk vektor?

Dia Produk silang, Juga dipanggil produk vektor, ia adalah sejenis produk yang dijalankan di antara dua vektor dan hasil dalam vektor lain, tegak lurus ke satah yang ditakrifkan oleh dua yang pertama.

Produk silang antara dua vektor ke dan b, Ia menghasilkan vektor lain R, Matematik ditulis seperti berikut:

ke × b = R

Ia berbunyi seperti ini: "A cruz b sama dengan r ".

Dalam teks bercetak, vektor ditulis dengan lirik berani, atau dengan anak panah pada surat, untuk membezakannya dari magnitud atau modul mereka. Untuk ini mereka digunakan, secara bergantian, bar modul dan huruf semasa, jadi nilai mutlak vektor ke Simbol ditulis seperti ini:

│ke│ = a

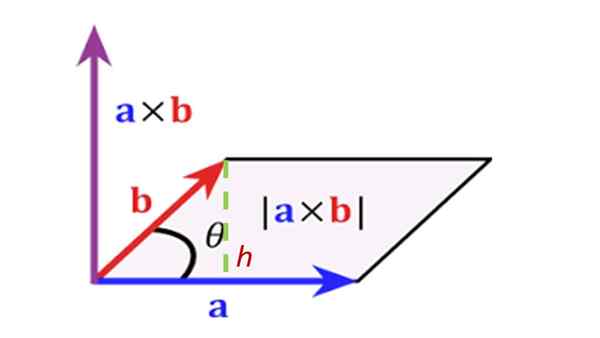
Nilai mutlak atau modul produk vektor antara dua vektor dikira dengan mengalikan modul kedua -dua vektor melalui sudut θ di antara mereka:

R = a ∙ b ∙ sen θ

Arah vektor R Ia berserenjang dengan vektor ke dan b. Rasa R Ia adalah dextrogyr dari ke ke arah b Dan dalam praktiknya ditentukan menggunakan peraturan tangan kanan, yang terdiri daripada kedudukan indeks, sederhana dan ibu jari tangan kanan seperti berikut:

• Jari telunjuk diletakkan mengikut vektor ke
• Dengan jari tengah mengikuti vektor b
• Jempol, dilanjutkan, menunjukkan arah dan arah vektor R.

Perintah ini mesti diikuti dengan tepat, kerana produk vektor tidak komutatif, iaitu ke × b ≠ b × ke Dan jika vektor ditukar, hasil yang betul tidak akan diperoleh.

Boleh melayani anda: Teorem kewujudan dan keunikan: demonstrasi, contoh dan latihan

Pembaca dinasihatkan untuk meletakkan tangan kanannya sebagai angka menunjukkan, indeks yang menunjuk ke kiri mewakili vektor ke, Jari tengah mengikuti b Dan ia menunjukkan terus kepada pembaca, akhirnya, ibu jari menunjukkan, menunjuk ke arah dan arah vektor ke × b = R.

Ciri -ciri produk Cruz

-Produk salib atau vektor antara dua vektor selalu menghasilkan vektor lain.

-Oleh itu, produk silang bukan komutatif, oleh itu: ke × b ≠ b × ke.

-Untuk produk silang itu benar bahawa: ke × b = - (b × ke). Harta ini dipanggil Anti-Kon-Konkrim.

-Vektor produk vektor yang dihasilkan antara dua vektor adalah tegak lurus (normal) kepada vektor tersebut.

-Dari yang di atas ia mengikuti bahawa produk vektor antara vektor dengan arah yang sama adalah batal. Khususnya ke × A = 0.

-Produk silang mematuhi undang -undang pengedaran berkenaan dengan jumlah: ke × (b+c) = ke × b + ke × c

-Jika m adalah skalar, maka m (ke × b) = m ke × b = ke × m b

Produk silang antara vektor unit

Tiga vektor unit, yang dipanggil Yo, J dan k, Mereka berserenjang antara satu sama lain dan menunjukkan tiga arah yang ketara ruang: tinggi, lebar dan mendalam. Alamat ini berserenjang antara satu sama lain.

Produk vektor antara vektor unit mudah ditentukan melalui peraturan tangan kanan dan mengingati sifat produk salib:

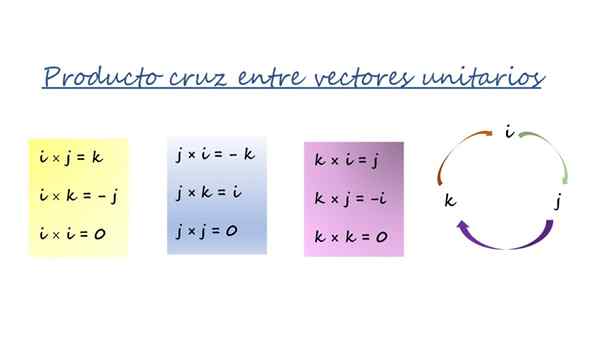Produk vektor vektor unit Cartesian. Sumber: f. Zapata.

Tiga kotak berwarna dalam angka diringkaskan dalam pusingan dengan anak panah ke kanan dan digunakan dengan cara ini:

-Apabila mengalikan ke arah anak panah, hasilnya adalah vektor di hadapan anak panah dan mempunyai tanda positif. Contohnya, dengan mengalikan vektor J dan k, Vektor ketiga adalah Yo, Dan sebagai perintah mengikuti makna anak panah, tanda itu +.

Boleh melayani anda: fungsi vektor

-Dan jika ia berlipat ganda ke arah yang bertentangan dengan anak panah, hasilnya adalah vektor ketiga di hadapan anak panah, tetapi dengan tanda negatif.

Vektor unit merupakan asas, jadi mana -mana vektor lain boleh ditulis dari segi mereka. Ini sangat memudahkan pengiraan produk silang antara dua vektor sewenang -wenangnya di ruang angkasa.

Cara Menganalisis Produk Salib Dua Vektor Analitik

Apabila vektor ke dan b Mereka mempunyai arah sewenang -wenang di angkasa, dengan komponen di sepanjang setiap mereka, lebih mudah untuk mengira produk silang dengan cara analisis, menyatakannya dari segi vektor unit Yo, J dan k:

• ke = a_x Yo + ke_dan J + ke_z k
• b = b_x Yo + b_dan J + b_z k

Sekarang harta pendaraban pengedaran digunakan, yang juga sah untuk produk silang:

ke × b = (a_x Yo + ke_dan J + ke_z k) × (b_x Yo + b_dan J + b_z k) =

= (a_x Yo × b_x Yo) + (a_x Yo × b_dan J) + (a_x Yo × b_z k) + (a_Dan J × b_x Yo) + (a_Dan J × b_dan J) + (a_Dan J × b_z k) + (a_Z k × b_x Yo) + (a_Z k × b_dan J) + (a_Z k × b_z k)

Produk silang antara vektor unit yang sama dibatalkan, kerana ia adalah vektor selari, yang mengurangkan ungkapan ini kepada 6 istilah:

ke × b = (a_x Yo × b_dan J) + (a_x Yo × b_z k) + (a_Dan J × b_x Yo) + (a_Dan J × b_z k) + (a_Z k × b_x Yo) + (a_Z k × b_dan J)

Akhirnya, menggunakan angka di atas, setiap produk menghasilkan:

ke × b = a_x b_dan k + ke_x b_z ( -J) + a_Dan b_x ( -k) + a_Dan b_z Yo + ke_Z b_xJ + ke_Z b_dan ( -Yo) =

= (a_Dan b_z - a_Z b_dan) Yo + (Kepada_Z b_x - a_x b_z) J + (Kepada_x b_dan - a_Dan b_x) k

Produk cruz melalui penentu

Ia tidak perlu menghafal formula di atas, tetapi dengan mudah memohon pusingan angka terdahulu atau hanya dengan teliti menjalankan penentu yang ditunjukkan di bawah, yang sama sekali setara:

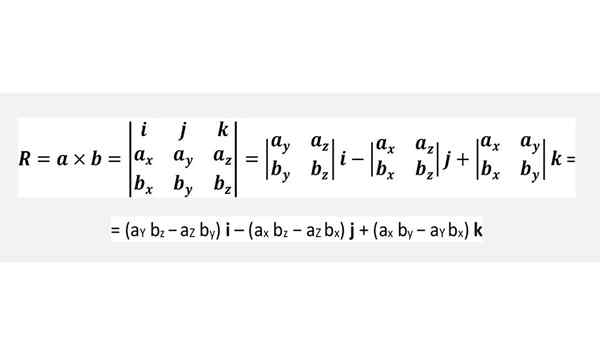
Contoh

Menganggap vektor ke dan b adalah:

• ke = 5 Yo - J + 4 k
• b = -Yo + 0J +7 k

Produk silang di antara mereka dikira dengan mengenal pasti dan menggantikan koordinat masing -masing:

Boleh melayani anda: Paraboloid hiperbolik: Definisi, sifat dan contoh

ke_x = 5; ke_dan = -1; ke_z = 4; b_x = -1; b_dan = 0: b_z = 7

ke × b = [(-1) ∙ 7 - 4 ∙ 0] Yo + [(4 ∙ (-1) - 5 ∙ 7) J + [5 ∙ 0 - (-1) ∙ (-1)] k = [-7 - 0] Yo + [(-4 - 35) J + [0 - 1] k =

= (-7) Yo - 39 J - k

Kaedah penentu menawarkan hasil yang sama.

Senaman

Hitung oleh penentu, produk silang di kalangan vektor:

• atau = 2 Yo +J + 5 k
• v = Yo + 4J +7 k

Dan tentukan kawasan paralelogram yang disembur oleh vektor terdahulu, seperti yang ditunjukkan dalam gambar:

Penyelesaian

Nilai koordinat vektor digantikan dalam penentu:

Kawasan paralelogram yang ditentukan adalah modul produk vektor di antara mereka, menghasilkan: r = 17.3 unit kawasan.